TICS-411 Minería de Datos

Clase 11: Naive Bayes

Alfonso Tobar-Arancibia

Naive Bayes: Preliminares

También conocido como Clasificador Inexperto de Bayes, es uno de los clasificadores más conocidos y sencillos.

Se hizo particularmente conocido como uno de los primeros algoritmos en funcionar como Clasificador de Spam de manera efectiva.

  • Es un modelo netamente probabilístico basado en el Teorema de Bayes.
    • Aprende una distribucional de Probabilidad Condicional.
    • Dado un punto \(x_i\), el modelo retorna la “probabilidad” de que \(x_i\) pertenezca a una clase específica.

Definiciones

Probabilidad Condicional
\[P(X|C) = \frac{P(X \cap C)}{P(C)}\]
Teorema de Bayes
\[P(C|X) = \frac{P(X|C)P(C)}{P(X)}\]
Independencia Condicional
\[P(X_1, X_2, ..., X_k|C) = \prod_{i=1}^k P(X_i|C)\]


Se lee como la Probabilidad de que Ocurra \(X\) dado que tenemos \(C\).


La probabilidad a posteriori (LHS), depende de el Likelihood, la probabilidad a priori y la evidencia (RHS).


Si asumimos independencia, entonces la probabilidad conjunta de \(k\) eventos condicionados, se calcula como la productoria de las probabilidades condicionales independientes.

Ejemplo básico

Supongamos que:

  • Sabemos que la Meningitis produce Tortícolis el 50% de las veces.
  • La probabilidad de tener meningitis es: \(1/50000\).
  • La probabilidad de tener Tortícolis: \(1/20\).

Si su paciente tiene tortícolis, ¿Cuál es la probabilidad de que tenga Meningitis?

\[P(M|T) = \frac{P(T|M)P(M)}{P(T)}=\frac{0.5 \cdot 1/50000}{1/20} = 0.0002\]

Modelo Naive Bayes: Aprendizaje

\[P(y = C_j|X_1, X_2, ..., X_k) = \frac{P(X_1,X_2,..., X_k|y=C_j)P(y=C_j)}{P(X_1, X_2, ..., X_k)}\]

  • \(P(y=C_j|X)\) sería la probabilidad de que la predicción del modelo sea \(C_j\) dado que lo alimentamos con las variables \(X\).
  • Luego \(P(y=C_j)\) es la probabilidad a priori de que la clase sea \(C_j\).
  • \(P(X|y=C_j)\) es el likelihood (verosimilitud). Corresponde a la distribución de probabilidad de las variables X cuando la clase es \(C_j\).
  • \(P(X)\) es la evidencia, y normalmente es muy complejo de calcular.

Por simplicidad reduciremos \(X_1, X_2, ..., X_k\) a \(X\).

\(P(X)\) tiene como única función la de normalizar la probabilidad para que vaya en un rango entre 0 y 1.

Modelo Naive Bayes: Predicción

\[\hat{y_i} = \underset{C_j}{argmax} \: P(y=C_j|X) \]

donde, \[P(y = C_j|X) \propto \prod_{i=1}^k P(X|y=C_j)P(y=C_j)\]

La predicción de Naive Bayes corresponde a la clase que entrega [un estimado de] la Probabilidad a Posteriori más grande.

Ejemplo

¿Cómo clasificamos el siguiente punto?

\[ X = [C=Soleado,T=Media,H=Alta,V=Débil]\]

Probabilidad de Sí

\[P(y = Sí|X) = P(X|y=Sí)P(y=Sí)\]

Probabilidad de No

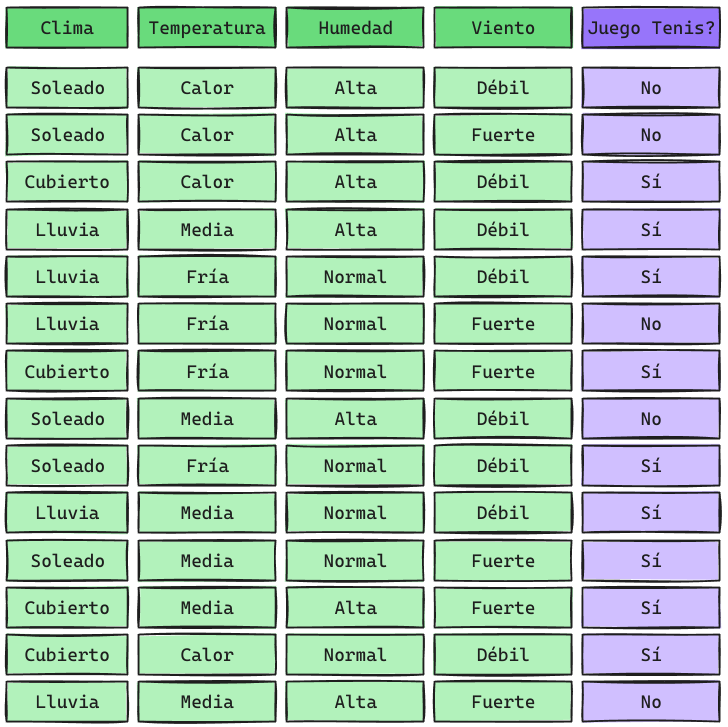
\[ P(y = No|X) = P(X|y=No)P(y=No)\]

Ejemplo

\[ P(y = Sí|X) = P(C=Soleado|y=Sí)P(T=Media|y=Sí)P(H=Alta|y=Sí)P(V=Débil|y=Sí)P(y=Sí)\]

\[ P(y = No|X) = P(C=Soleado|y=No)P(T=Media|y=No)P(H=Alta|y=No)P(V=Débil|y=No)P(y=No)\]

Probabilidad Condicional para clase Sí

\[\small P(C = Soleado|y = Sí) = 2/9\] \[\small P(T = Media|y = Sí) = 4/9\]

\[\small P(H = Alta|y = Sí) = 3/9\] \[\small P(V=Débil|y = Sí) = 6/9\]

Probabilidad Condicional para clase No

\[\small P(C = Soleado|y = No) = 3/5\] \[\small P(T = Media|y = No) = 2/5\]

\[\small P(H = Alta|y = No) = 4/5\] \[\small P(V=Débil|y = No) = 2/5\]

Probabilidad a priori

\[P(y = Sí) = \frac{9}{14} = 0.642\] \[P(y = No) = \frac{5}{14} = 0.357\]

Predicción

\[\scriptsize P(y = Sí|X) = P(C=Soleado|y=Sí)P(T=Media|y=Sí)P(H=Alta|y=Sí)P(V=Débil|y=Sí)P(y=Sí)\] \[\small P(y = Sí|X) = \frac{2}{9} \cdot \frac{4}{9} \cdot \frac{3}{9} \cdot \frac{6}{9} \cdot \frac{9}{14} = 0.0141\]

\[\scriptsize P(y = No|X) = P(C=Soleado|y=No)P(T=Media|y=No)P(H=Alta|y=No)P(V=Débil|y=No)P(y=No)\] \[\small P(y = No|X) = \frac{3}{5} \cdot \frac{2}{5} \cdot \frac{4}{5} \cdot \frac{2}{5} \cdot \frac{5}{14} = 0.0274\]

\[\hat{y} = argmax \{0.0141, 0.0274\} = No\]

Smoothing

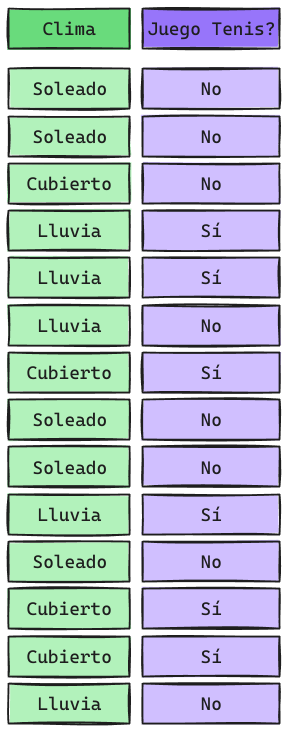
Supongamos otro dataset más pequeño:

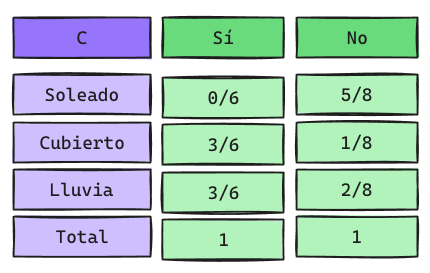
Dado que Naive Bayes se calcula como una Productoria, al tener probabilidades 0 inmediatamente la Probabilidad a Posteriori es 0.

\[ P(Clima = Soleado|y = Sí) = \frac{0}{6}\] \[ P(Clima = Soleado|y = No) = \frac{5}{8}\]

\[P(X_j|C = i) = \frac{N_{yj} + \alpha}{N_y + M\alpha}\]

  • \(\alpha\): Es un Hiperparámetro. Si \(\alpha = 1\) se le llama Laplace Smoothing, si \(\alpha <1\) entonces se le llama Lidstone Smoothing.
  • M: Corresponde al número de posibles valores que puede tomar \(X_j\)
  • \(N_{yj}\): Corresponde a la cantidad de registros que toman el valor de la variable \(X_j\) solicitado en la clase \(y\).
  • \(N_{y}\): Corresponde a la cantidad de registros totales que tienen la clase \(y\).

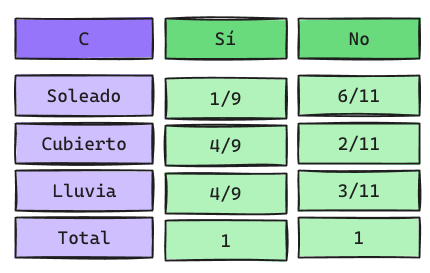
Laplace Smoothing

Sin Laplace

Con Laplace

En este caso \(\alpha = 1\) y \(M=3\) ya que Clima puede tomar 3 valores: Soleado, Cubierto y Lluvia.

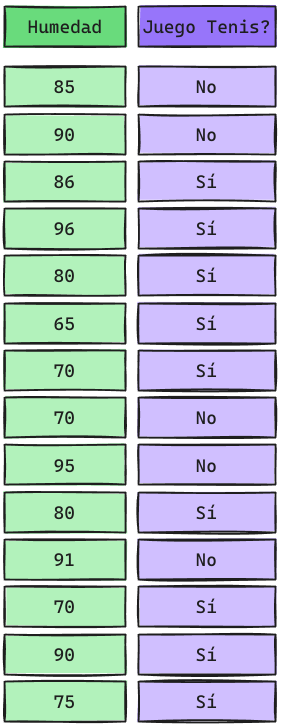
Variables Continuas

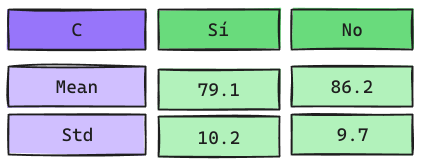
Podemos calcular el Likelihood como una PDF (Probability Density Function). La más común: Distribución Normal (Gaussian Naive Bayes).

\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Variables Continuas: Predicción

\[P(humedad=74|y = Sí) = \frac{1}{\sqrt{2\pi \cdot 10.2^2}}e^{-\frac{(74-79.1)^2}{2\cdot 10.2^2}} = 0.0345 \]

\[P(humedad=74|y = No) = \frac{1}{\sqrt{2\pi \cdot 9.7^2}}e^{-\frac{(74-86.2)^2}{2\cdot 9.7^2}} = 0.01865 \]

Luego la predicción es Sí.

Detalles Técnicos

Fortalezas

  • Fácil de Implementar
  • A menudo tiene un rendimiento decente a pesar de que las variables pueden no ser independientes.
  • Puede aprender de forma incremental.
  • Valores faltantes son ignorados en el proceso de Aprendizaje.
  • Modelo robusto frente a datos atípicos y/o irrelevantes.

Debilidades

  • Asumir clases condicionadas produce probabilidades sesgadas.
  • Dependencias entre las variables no pueden ser modeladas.

Implementación en Scikit-Learn

Multinomial Naive Bayes (Normal)

from sklearn.naive_bayes import MultinomialNB

nb = MultinomialNB(alpha = 1)
nb.fit(X_train, y_train)

y_pred = nb.predict(X_test)
y_proba = nb.predict_proba(X_test)

Gaussian Naive Bayes

from sklearn.naive_bayes import GaussianNB

gb = GaussianNB()
gb.fit(X_train, y_train)

y_pred = gb.predict(X_test)
y_proba = gb.predict_proba(X_test)

Adeus

Tics-411 Minería de Datos está licenciado bajo CC BY-NC-SA 4.0