TICS-411 Minería de Datos

Clase 3: Modelación Descriptiva y K-Means

Alfonso Tobar-Arancibia

Modelación Descriptiva (Aprendizaje no Supervisado)

Definiciones

Aprendizaje No supervisado

Es un tipo de aprendizaje que no requiere de etiquetas (las respuestas correctas) para poder aprender.

En nuestro caso nos enfocaremos en un caso particular de Modelación Descriptiva llamada Clustering.

Clustering

Consiste en agrupar los datos en un menor número de entidades o grupos. A estos grupos se les conoce como clusters y pueden ser generados de manera global, o modelando las principales características de los datos.

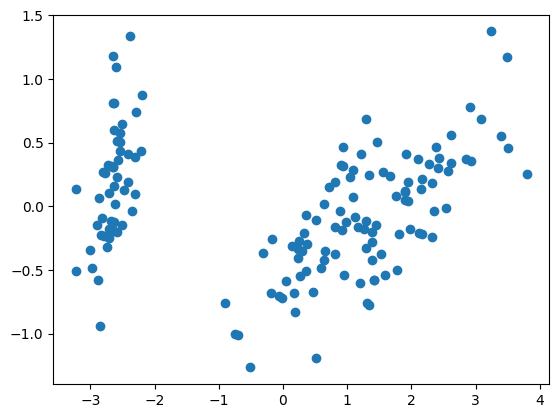
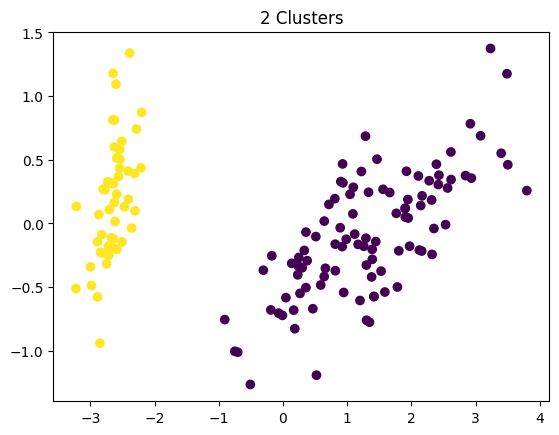
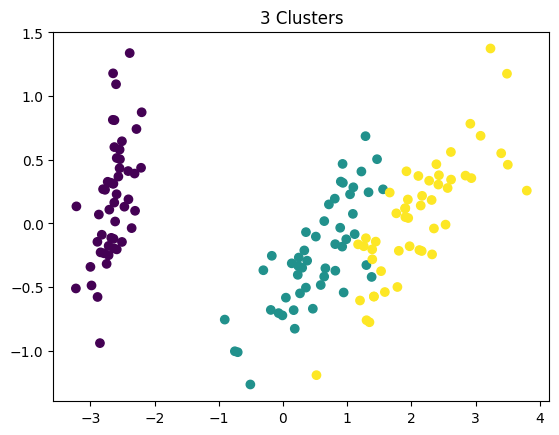
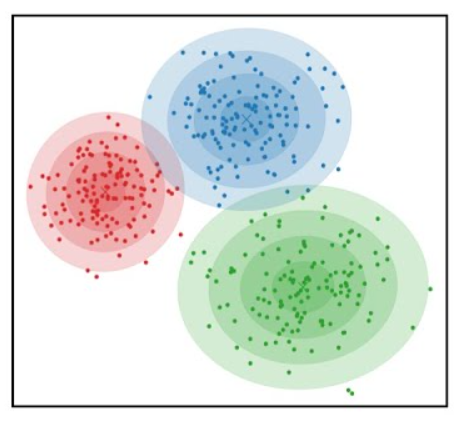
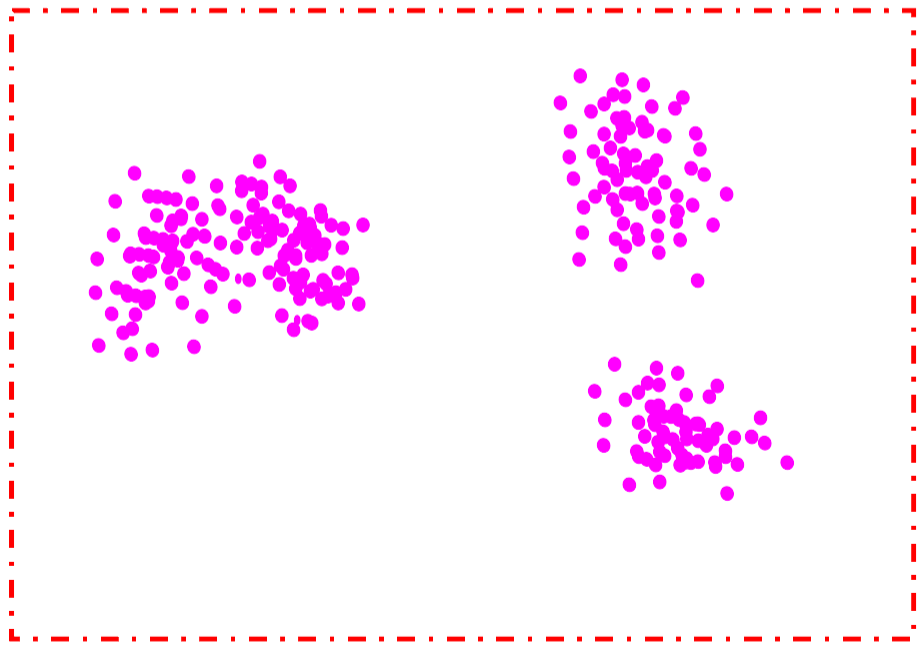
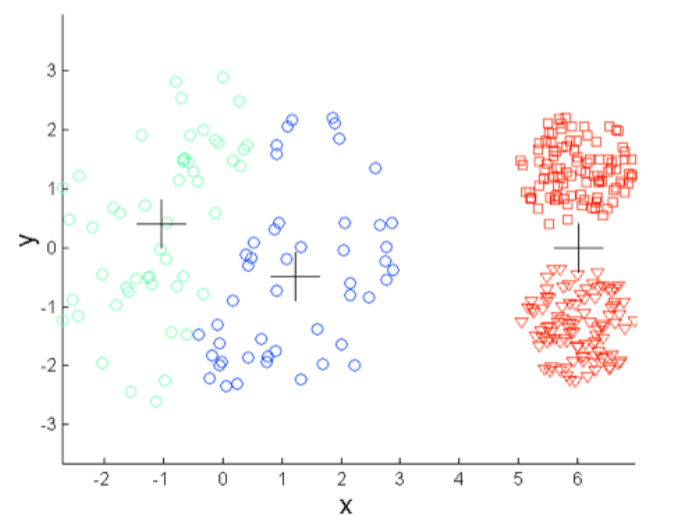
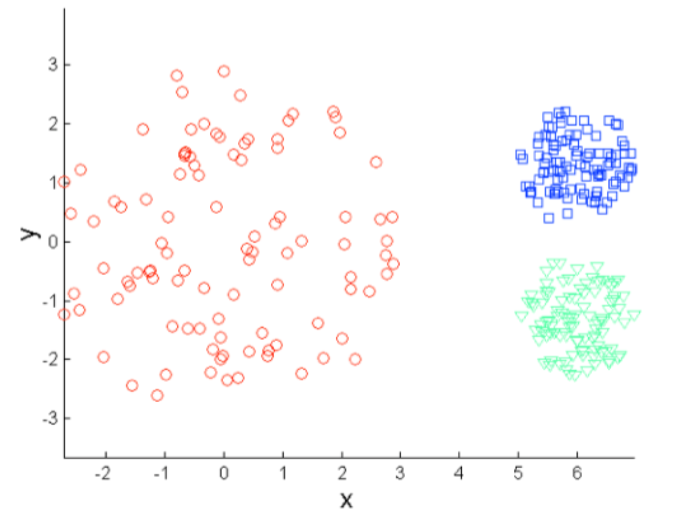
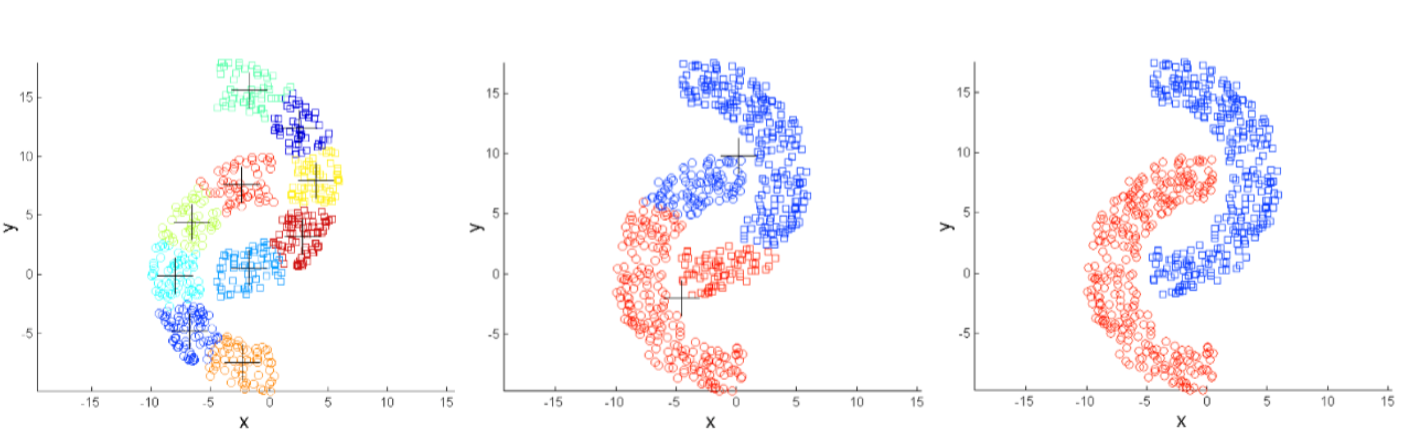
Intuición

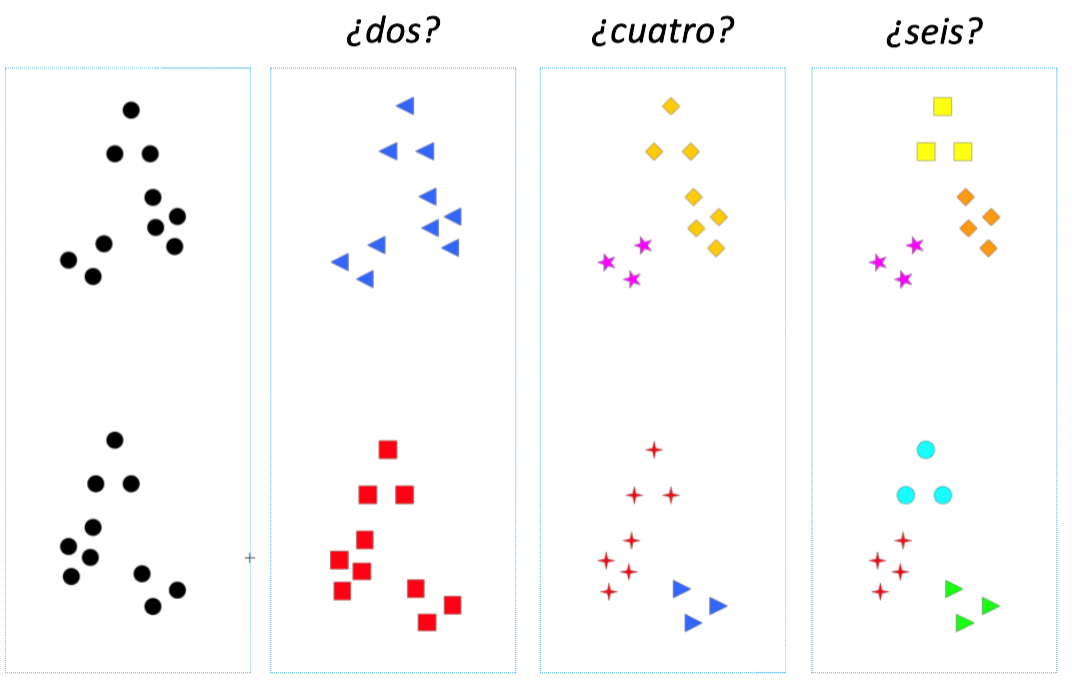
¿Cuántos clusters se pueden apreciar?

Clustering

Clustering: Introducción

Clustering: Consiste en buscar grupos de objetos tales que la similaridad intra-grupo sea alta, mientras que la similaridad inter-grupos sea baja. Normalmente la distancia es usada para determinar qué tan similares son estos grupos.

Clustering: Evaluación

  • Evaluar el nivel del éxito o logro del Clustering es complicado. ¿Por qué?

Clustering: Tipos


Clustering: Partición

Los datos son separados en K clusters, donde cada punto pertenece exclusivamente a un único cluster.

Clustering: Densidad

Se basan en la idea de continuar el crecimiento de un cluster a medida que la densidad (número de objetos o puntos) en el vecindario sobrepase algún umbral.

Clustering: Jerarquía

Los algoritmos basados en jerarquía pueden seguir 2 estrategias:

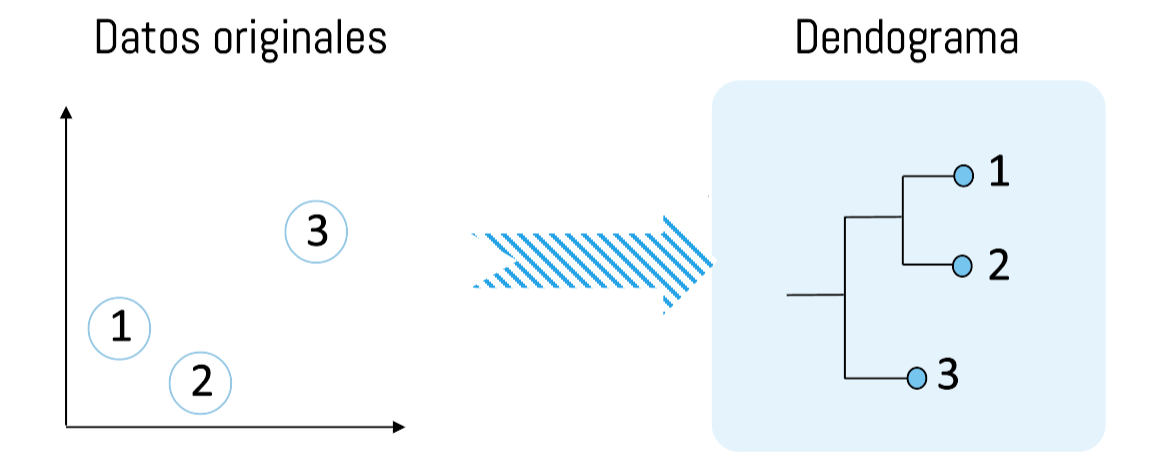
  • Aglomerativos: Comienzan con cada objeto como un grupo (bottom-up). Estos grupos se van combinando sucesivamente a través de una métrica de similaridad. Para n objetos se realizan n-1 uniones.

  • Divisionales: Comienzan con un solo gran cluster (bottom-down). Posteriormente este mega-cluster es dividido sucesivamente de acuerdo a una métrica de similaridad.

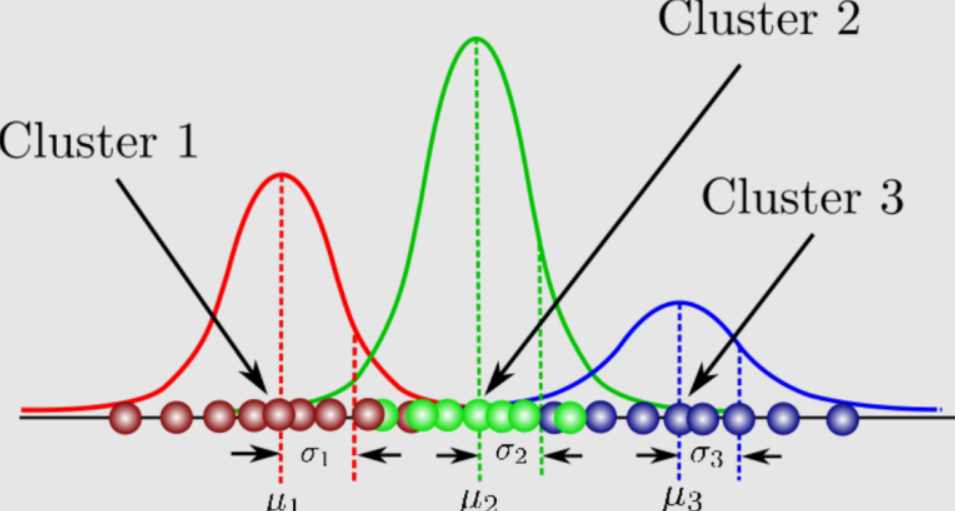
Clustering: Probabilístico

Se ajusta cada punto a una distribución de probabilidades que indica cuál es la probabilidad de pertenencia a dicho cluster.

Métodos Basados en Partición

Partición

Los datos son separados en K Clusters, donde cada punto pertenece exclusivamente a un único cluster. A K se le considera como un hiperparámetro.

  • Cluster Compactos: Minimizar la distancia intra-cluster (within cluster).
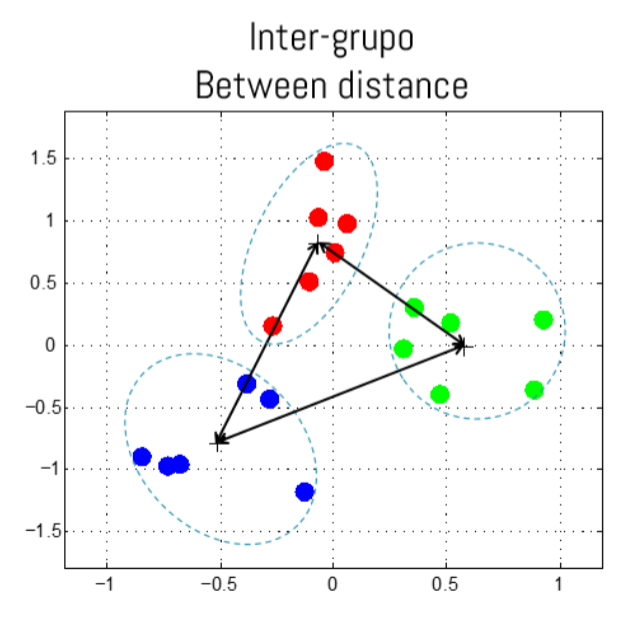
  • Clusters bien separados: Maximizar la distancia inter-cluster (between cluster).

\[ Score (C,D) = f(wc(C),bc(C))\]

El puntaje/score mide la calidad del clustering \(C\) para el Dataset \(D\).

Score

\[ Score (C,D) = f(wc(C),bc(C))\]


  • Distancia Between-Cluster: \[bc(C) = \sum_{1 \le j \le k \le K} d(r_j, r_k)\]

donde \(r_k\) representa el centro del cluster \(k\): \[r_k = \frac{1}{n_k} \sum_{x_i \in C_k} x_i\]

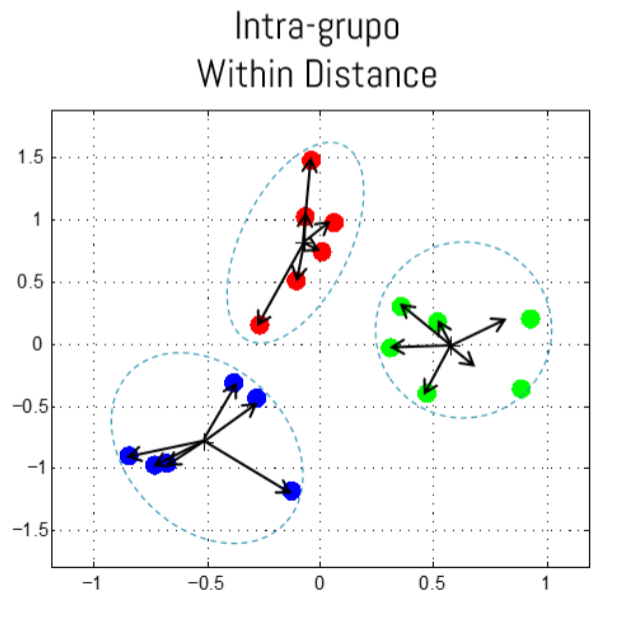
  • Distancia Within-Cluster (Inercia): \[wc(C) = \sum_{k=1}^K \sum_{x_i \in C_k} d(x_i, r_k)\]

Distancia entre los centros de cada cluster.

Distancia entre todos los puntos del cluster y su respectivo centro.

K-Means

K-Means

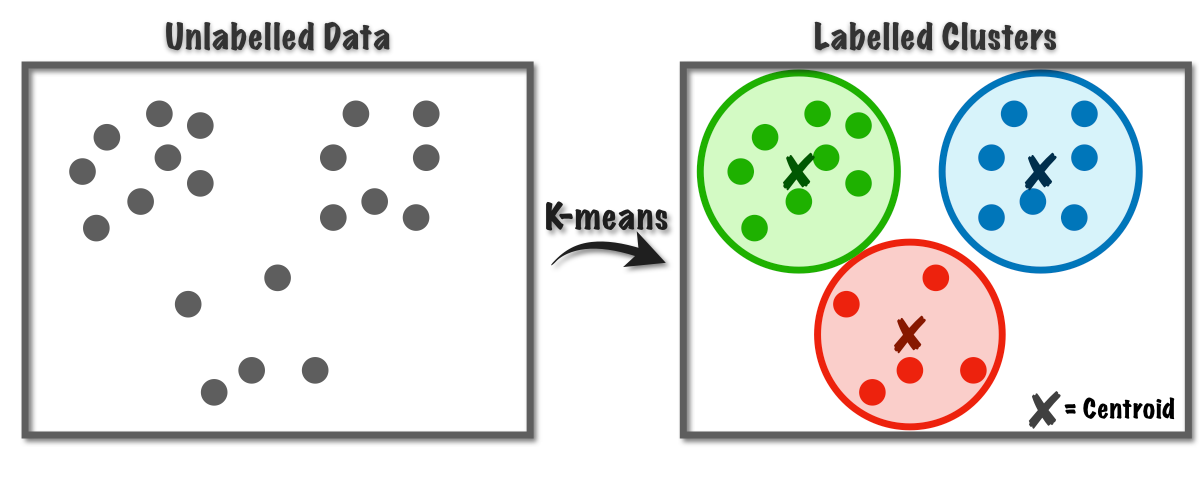
Dado un número de clusters \(K\) (determinado por el usuario), cada cluster es asociado a un centro (centroide). Luego, cada punto es asociado al cluster con el centroide más cercano.

Normalmente se utiliza la Distancia Euclideana como medida de similaridad.

  1. Se seleccionan \(K\) puntos como centroides iniciales.
  2. Repite:
    • Forma K clusters asignando todos los puntos al centroide más cercano.
    • Recalcula el centroide para cada clase como la media de todos los puntos de dicho cluster.
  • Se repite este procedimiento por un número finito de iteraciones o hasta que los centroides no cambien.

K-Means: Ejemplo

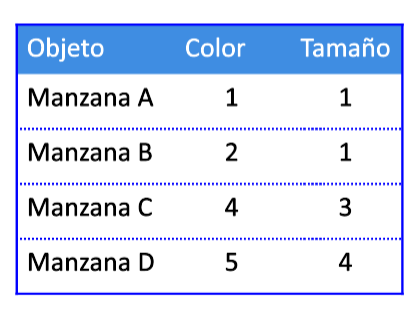
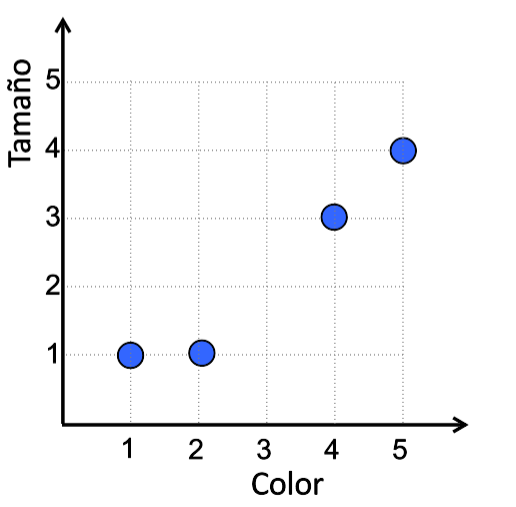
Resolvamos el siguiente ejemplo.

Supongamos que tenemos tipos de manzana, y cada una de ellas tiene 2 atributos (features). Agrupemos estos objetos en 2 grupos de manzanas basados en sus características.

K-Means: Ejemplo

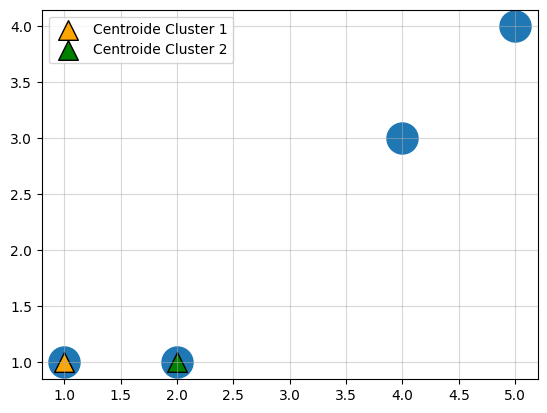
1era Iteración

  • Supongamos los siguientes centroides iniciales: \[C_1 = (1,1)\] \[C_2 = (2,1)\]

Matriz de Distancias al Centroide: (coordenada i,j representa distancia del punto j al centroide i)

\[D^1 = \begin{bmatrix} 0 & 1 & 3.61 & 5\\ 1 & 0 & 2.83 & 4.24 \end{bmatrix}\]

  • Calculemos la Matriz de Pertenencia \(G\):

\[G^1 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \end{bmatrix}\]

Los nuevos centroides son: \[C_1 = (1,1)\] \[C_2 = (\frac{11}{3}, \frac{8}{3})\]

K-Means: Ejemplo

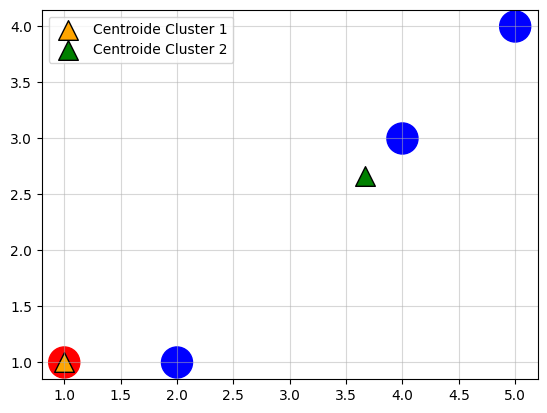
2da Iteración

  • Los nuevos centroides son:

\[C_1 = (1,1)\] \[C_2 = (\frac{11}{3}, \frac{8}{3})\]

  • Calculamos la Matriz de Distancias al Centroide:

\[D^2 = \begin{bmatrix} 0 & 1 & 3.61 & 5\\ 3.14 & 2.26 & 0.47 & 1.89 \end{bmatrix}\]

  • Calculemos la Matriz de Pertenencia \(G\):

\[G^2 = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix}\]

Los nuevos centroides son:

\(C_1 = (\frac{3}{2}, 1)\) y \(C_2 = (\frac{9}{2}, \frac{7}{2})\)

K-Means: Ejemplo

  • Si seguimos iterando notaremos que ya no hay cambios en los clusters. El algoritmo converge.
  • Este es el resultado de usar \(K=2\). Utilizar otro valor de \(K\) entregará valores distintos.
  • ¿Es este el número de clusters óptimos?

K-Means: Número de Clusters Óptimos

  • Siempre es posible encontrar el número de clusters indicados.
  • Entonces,

¿Cómo debería escoger el valor de \(K\)?

K-Means: Número de Clusters Óptimos

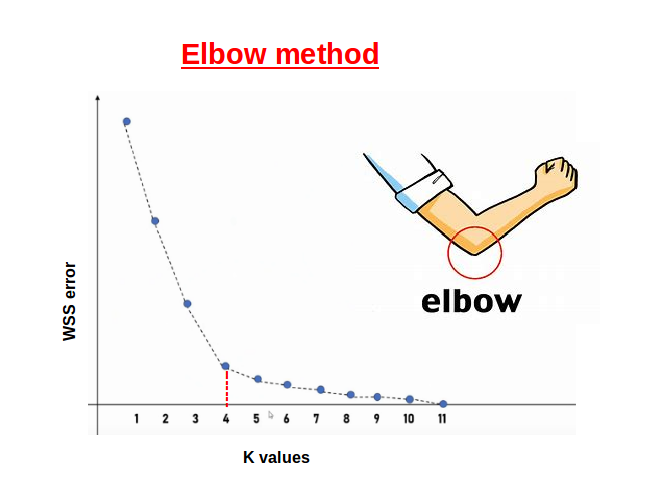
Curva del Codo
Es una heurísitca en la cual gráfica el valor de una métrica de distancia (e.g. within distance) para distintos valores de \(K\). El valor óptimo de \(K\) será el codo de la curva, que es el valor donde se estabiliza la métrica.


  • Este valor del codo muchas veces es subjetivo y distintas apreciaciones pueden llegar a distintos \(K\) óptimos.

Eventualmente otras métricas distintas al within cluster distance podrían también ser usadas.

¿Cuál es el efecto que está buscando la curva del codo? ¿Qué implica el valor de K escogido?

K-Means: Detalles Técnicos

Fortalezas

  • Algoritmo relativamente eficiente (\(O(k \cdot n \cdot i)\)). Donde \(k\) es el número de clusters, \(n\) el número de puntos, e \(i\) el número de iteraciones.
  • Encuentra “clusters esféricos”.

Debilidades

  • Sensible al punto de inicio.
  • Solo se puede aplicar cuando el promedio es calculable.
  • Se requiere definir K a priori (K es un hiperparámetro).
  • Suceptible al ruido y a mínimos locales (podría no converger).

Implementación en Scikit-Learn

from sklearn.cluster import KMeans

km = KMeans(n_clusters=8, n_init=10,random_state=None)
km.fit(X)
km.predict(X)

## opcionalmente
km.fit_predict(X)

  • n_clusters: Define el número de clusters a crear, por defecto 8.

  • n_init: Cuántas veces se ejecuta el algoritmo, por defecto 10.

  • random_state: Define la semilla aleatoria. Por defecto sin semilla.

  • init: Permite agregar centroides de manera manual.

  • .fit(): Entrenará el modelo en los datos suministrados.

  • .predict() Entregará las clusters asignados a cada dato suministrado.

  • .clusters_centers_: Entregará las coordenadas de los centroides de cada Cluster.

  • .inertia_: Entrega valores correspondiente a la within cluster distance.

👀 Veamos un ejemplo en Colab.

Sugerencias

Pre-procesamientos

Es importante recordar que K-Means es un Algoritmo basado en distancias, por lo tanto se ve afectado por Outliers y por Escala.

Se recomienda preprocesar los datos con:

  • Winsorizer() para eliminar Outliers.
  • StandardScaler() o MinMaxScaler() para llevar a una escala común.

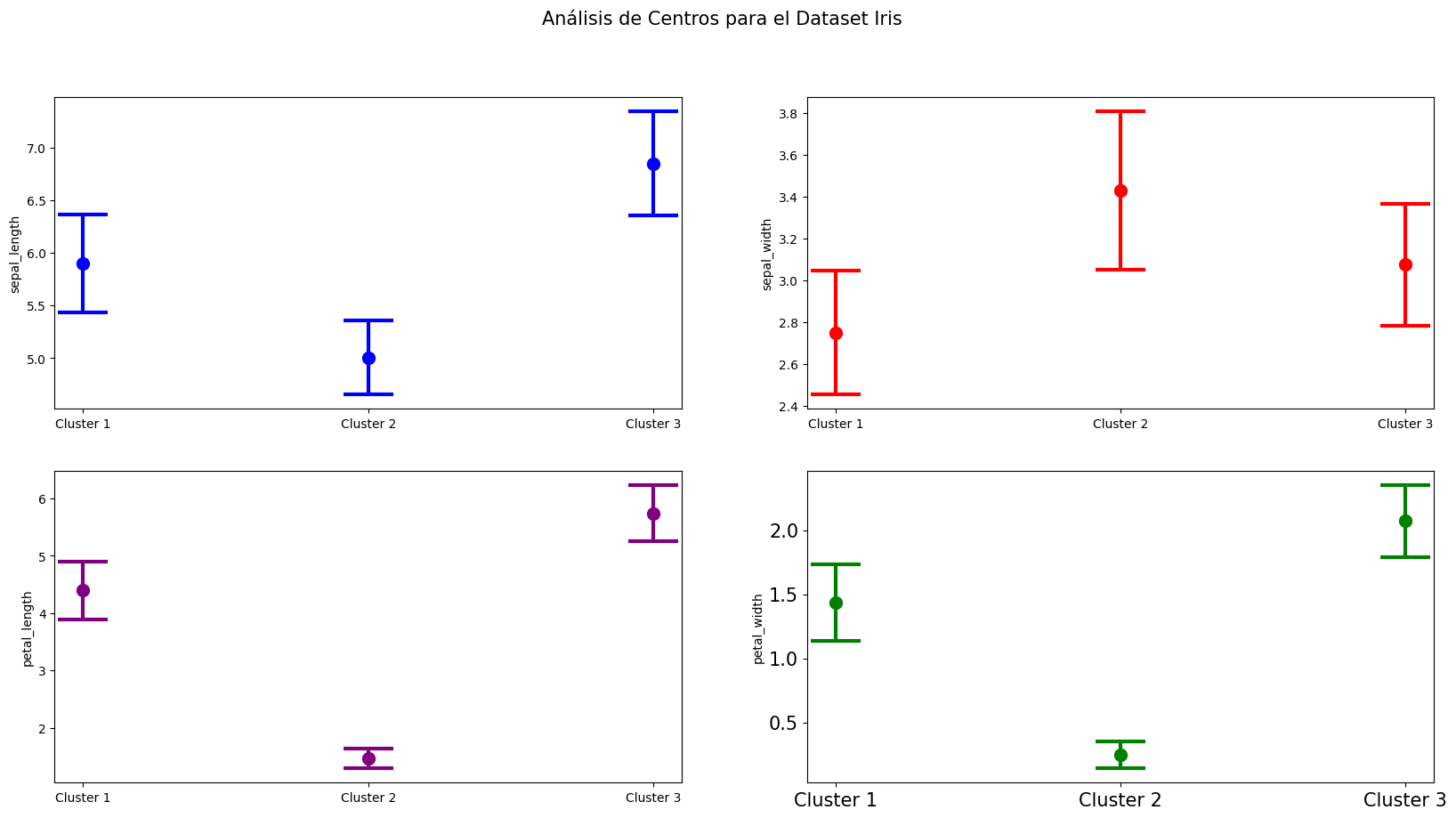
Interpretación Clusters

Recordar, que el clustering no clasifica. Por lo tanto, a pesar de que K-Means nos indica a qué cluster pertenece cierto punto, debemos interpretar cada cluster para entender qué es lo que se agrupó.

La interpretación del cluster es principalmente intuición y exploración, por lo tanto el EDA puede ser de utilidad para analizar clusters.

Post-Procesamiento: Merge

Post-Procesamiento

Se define como el tratamiento que podemos realizar al algoritmo luego de haber entregado ya sus predicciones.

Es posible generar más clusters de los necesarios y luego ir agrupando los más cercanos.

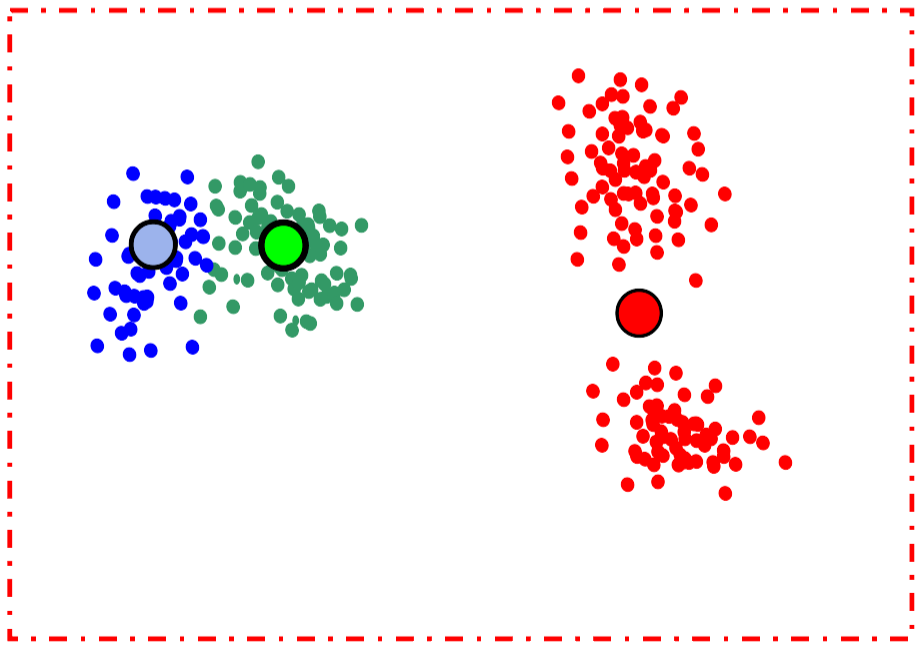
Post-Procesamiento: Merge

¿Cuál es el problema con este caso de Post-Procesamiento?

Post-Procesamiento: Split

En Scikit-Learn esto puede conseguirse utilizando el parámetro init. Se entregan los nuevos centroides para forzar a K-Means que separe ciertos clusters.

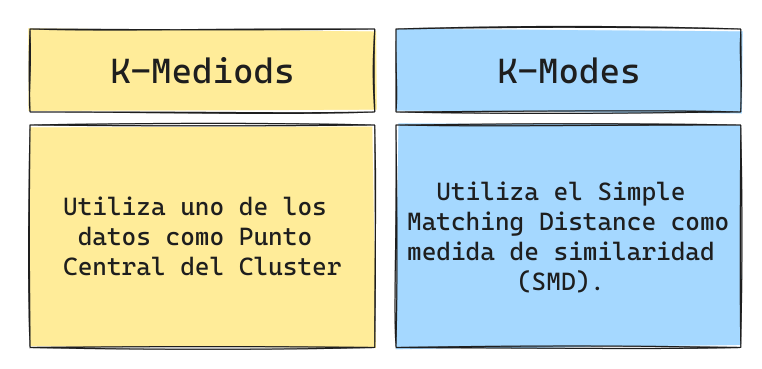
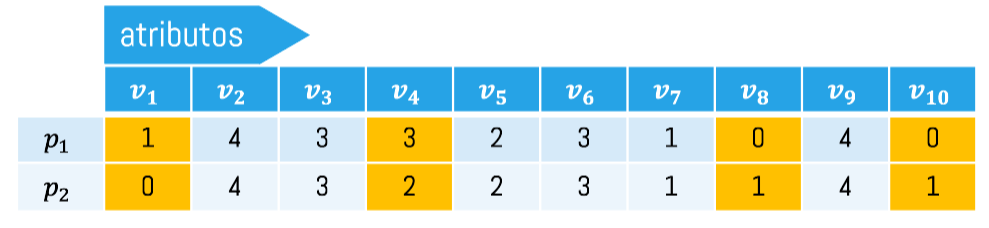
Variantes K-Means

\[SMD(p_1,p_2) = 4\]

Acá pueden encontrar una implementación de K-Modes en Python.

That’s all Folks

Tics-411 Minería de Datos está licenciado bajo CC BY-NC-SA 4.0