TICS-411 Minería de Datos

Clase 4: Clustering Jerárquico

Alfonso Tobar-Arancibia

Clustering Jerárquico

Definiciones

Clustering Jerárquico

Es un tipo de aprendizaje que no requiere de etiquetas (las respuestas correctas) para poder aprender. Se basa en la construcción de Jerarquías para ir construyendo clusters.

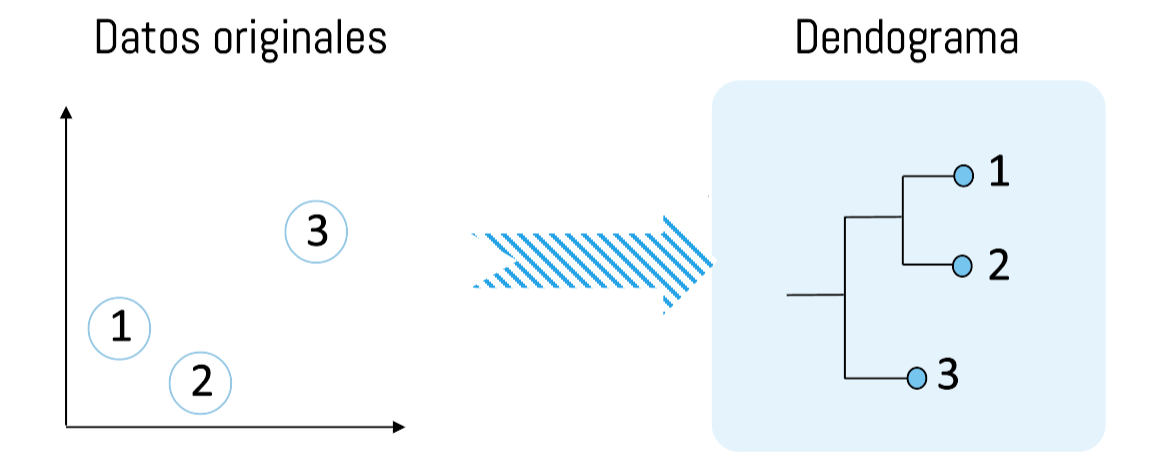
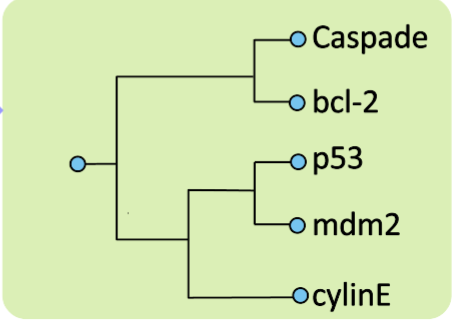
Dendograma

Corresponde a un diagrama en el que se muestran las distancias de atributos entre clases que son parte de un mismo cluster.

Clustering: Jerarquía

Los algoritmos basados en jerarquía pueden seguir 2 estrategias:

  • Aglomerativos: Comienzan con cada objeto como un grupo (bottom-up). Estos grupos se van combinando sucesivamente a través de una métrica de similaridad. Para n objetos se realizan n-1 uniones.

  • Divisionales: Comienzan con un solo gran cluster (bottom-down). Posteriormente este mega-cluster es dividido sucesivamente de acuerdo a una métrica de similaridad.

Clustering Aglomerativo

Clustering Aglomerativo: Algoritmo

Algoritmo

  1. Inicialmente se considera cada punto como un cluster.
  2. Calcula la matriz de proximidad/distancia entre cada cluster.
  3. Repetir (hasta que exista un solo cluster):
    • Unir los cluster más cercanos.
    • Actualizar la matriz de proximidad/distancia.

Lo más importante de este proceso es el cálculo de la matriz de proximidad/distancia entre clusters

Distintos enfoques de distancia entre clusters, segmentan los datos en forma distinta.

Clustering Aglomerativo: Ejemplo

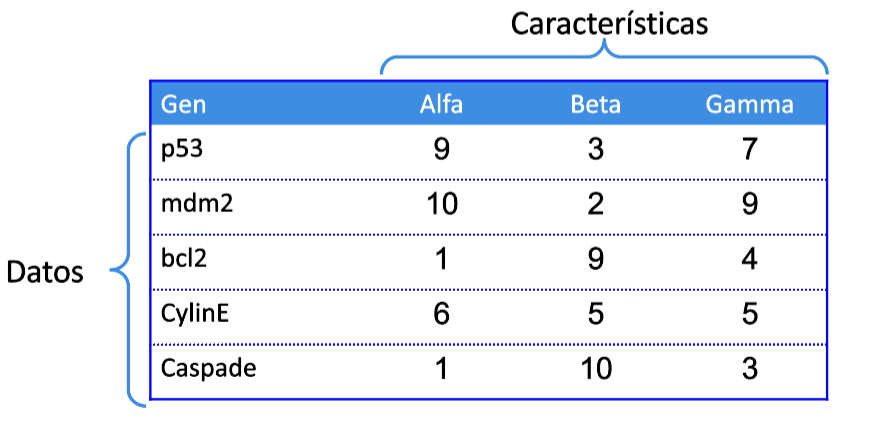
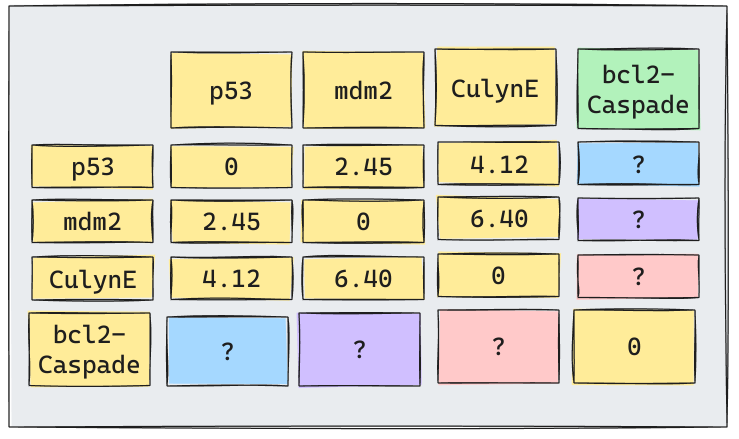
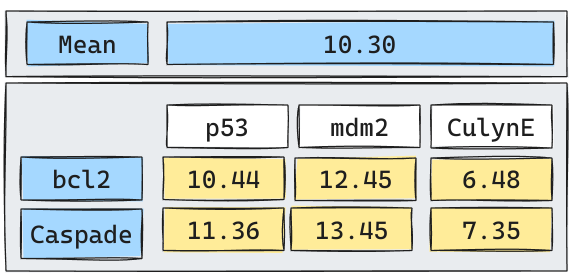
Supongamos que tenemos cinco tipos de genes cuya expresión ha sido determinada por 3 caracteríticas. Las siguientes expresiones pueden ser vistas como la expresión dados los genes en tres experimentos. ​

Apliquemos un Clustering Jerárquico Aglomerativo utilizando como medida de similaridad la Distancia Euclideana.

Otros tipos de distancia también son aplicables siguiendo un procedimiento análogo.

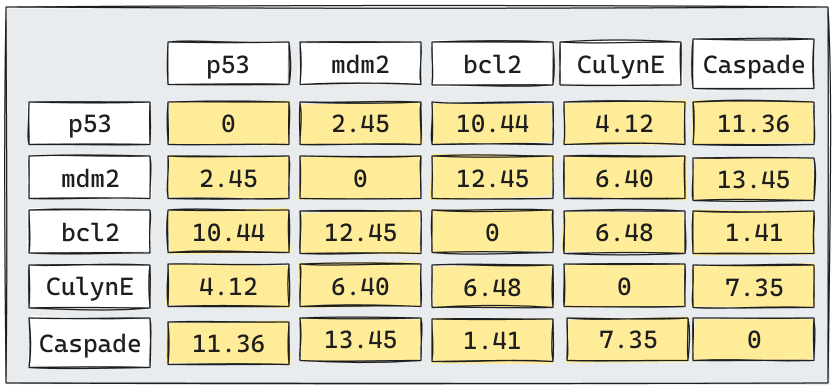
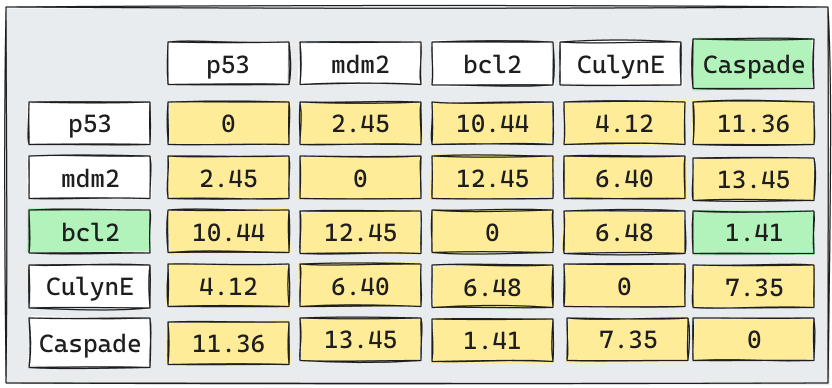
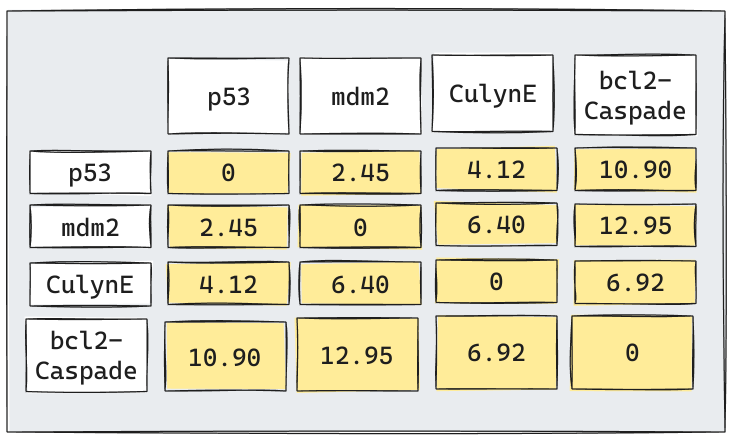
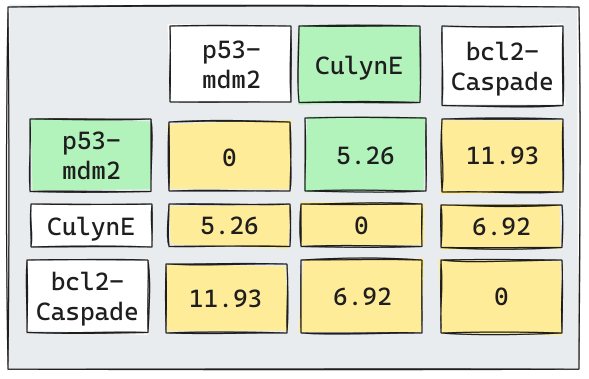
Algoritmo: 1era Iteración

El algoritmo considerará que todos los puntos inicialmente son un cluster. Por lo tanto, tratará de encontrar los 2 puntos más cercanos e intentará unirnos en un sólo cluster.

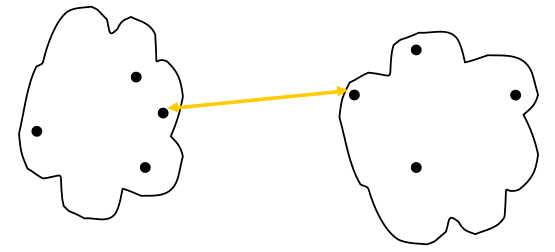
Problema: ¿Cómo actualizamos la matriz de Distancias?

Entonces crearemos un nuevo cluster: bcl2-Caspade.

Clustering Aglomerativo: Single Linkage

  • Distancia entre clusters determinada por los puntos más similares entre los clusters.

\[D(C_i, C_j) = min\{d(x,y) | x \in C_i, y \in C_j\}\]

Ventajas

  • Genera Clusters largos y delgados.

Limitaciones

  • Afectado por Outliers

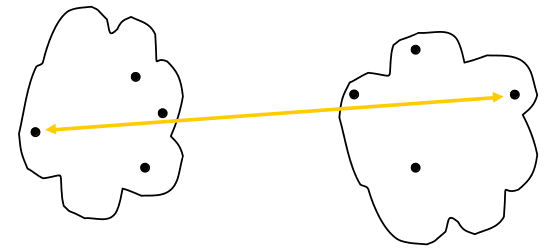
Clustering Aglomerativo: Complete Linkage

  • Distancia determinada por la distancia ente los puntos más disímiles entre los clusters.

\[D(C_i, C_j) = max\{d(x,y) | x \in C_i, y \in C_j\}\]

Ventajas

  • Menos suceptible a dato atípicos.

Limitaciones

  • Tiende a quebrar Clusters Grandes.
  • Tiene tendencia a generar Clusters circulares.

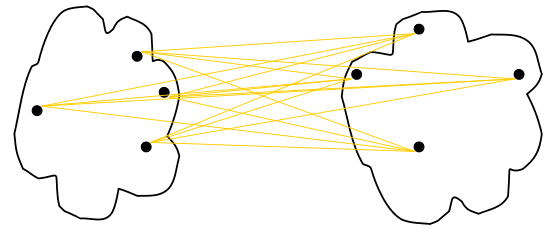
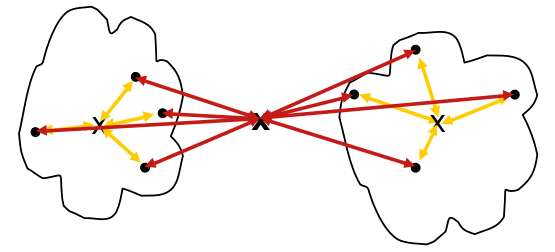
Clustering Aglomerativo: Average Linkage

  • Distancia determinada por el promedio de las distancias que componen los clusters.
  • Punto intermedio entre Single y Complete.

\[D(C_i, C_j) = avg\{d(x,y) | x \in C_i, y \in C_j\}\]

Ventajas

  • Menos suceptible a datos atípicos.

Limitaciones

  • Tiende a generar clusters circulares.

Clustering Aglomerativo: Ward Linkage

  • Distancia determinada por el incremento del Within cluster distance.
  • Minimiza la distancia intra cluster y maximiza la distancia entre clusters.

\[D(C_i, C_j) = wc(Cij) - wc(C_i) - wc(C_j) = \frac{n_i\cdot n_j}{n_i + n_j}||\bar{C_i} - \bar{C_j}||^2\]

Ventajas

  • Menos suceptible a dato atípicos.

Limitaciones

  • Tiende a generar clusters circulares.

Hiperparámetros

Los Hiperparámetros de este modelo serán:

Note

  • linkage: La forma de calcular la distancia entre clusters.
  • distancia: La distancia utilizada como similaridad entre los clusters.

A diferencia de K-Means, este método no requiere definir el número de Clusters a priori.

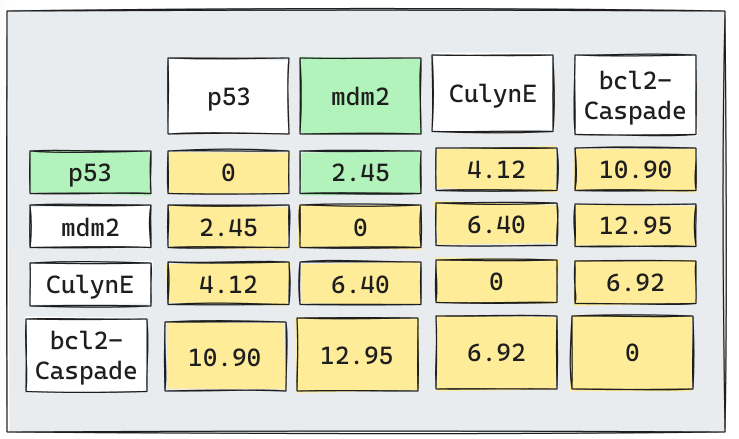
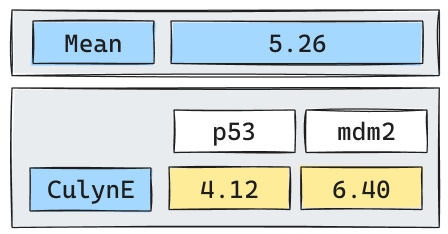
Volvamos a la Iteración 1

Supongamos que por simplicidad utilizaremos Average Linkage. (El proceso para utilizar otro linkage es análogo).

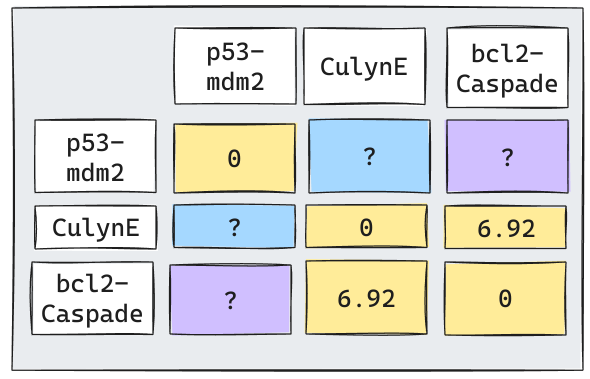
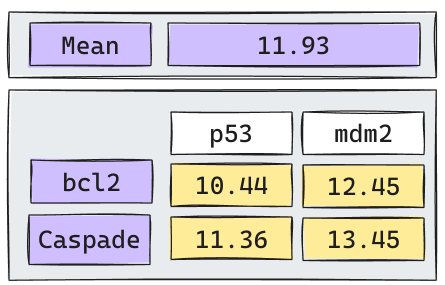
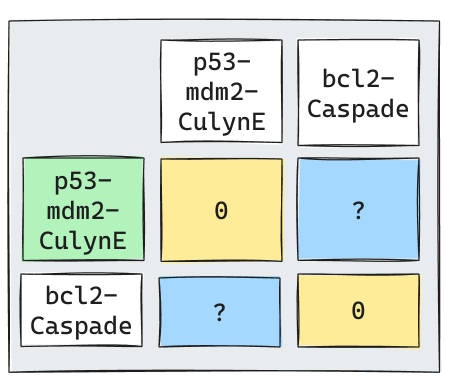
Vamos a extraer una Matriz entre los puntos a fusionar y los puntos de los clusters restantes.

Dendograma: 1era Iteración

Iteración 2

Dendograma: 2da Iteración

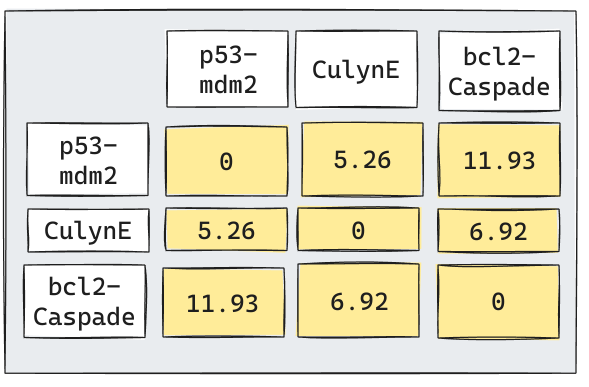
Iteración 3

Dendograma: 3ra Iteración

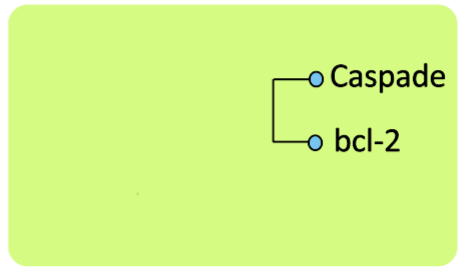
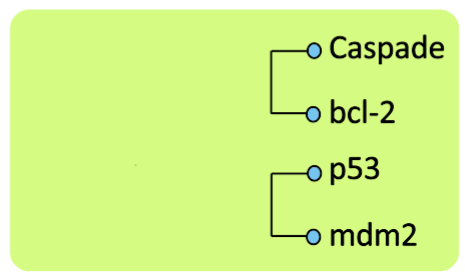
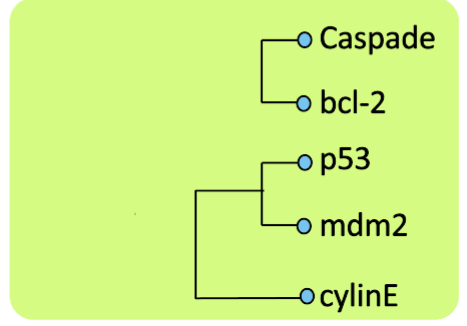
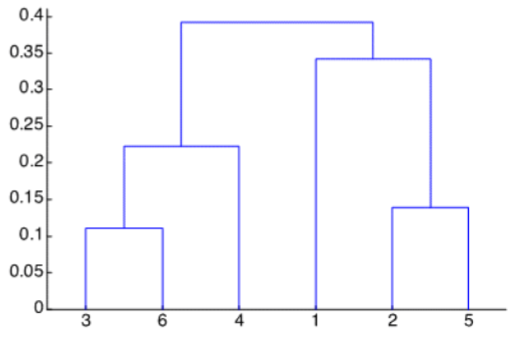
Dendograma Resultante

No es necesario realizar la última iteración ya que se entiende que ambos clusters se unen.

¿Cómo encontramos los clusters una vez que tenemos el Dendograma?

  • Podemos escoger un umbral de distancia y ver cuántos clusters se forman.
  • Como regla general se deben escoger clusters más distanciados entre sí.

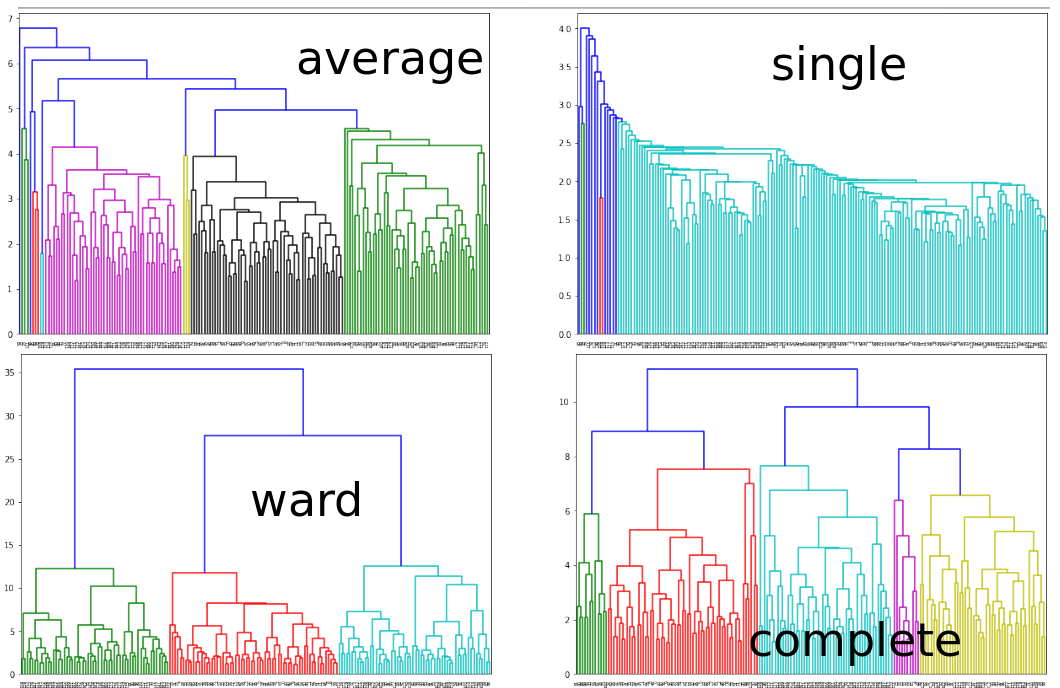
Efecto del Linkage Escogido

Clustering Jerárquico: Detalles Técnicos

Fortalezas

  • No requiere definir el número de Clusters a priori.
  • Al tener distintas variantes es posible que los puntos sean agrupados de manera completamente distintas.

Debilidades

  • Muy ineficiente computacionalmente debido a que genera una nueva matriz de distancia en cada iteración lo que entrega una complejidad \(O(n^2)\) o \(O(n^3)\) dependiendo del linkage.
  • Una vez que se decide combinar 2 clusters no es posible revertir esta decisión.
  • No tiene capacidad de generalización, ya que no es posible aplicarlo a datos nuevos.

Implementación en Scikit-Learn

from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters=2, metric="euclidean",linkage="ward")

## Se entrena y se genera la predicción
ac.fit_predict(X)

  • n_clusters: Define el número de clusters a crear, por defecto 2.

  • metric: Permite distancias L1, L2 y coseno. Por defecto “euclidean”.

  • linkage: Permite single, complete, average y ward. Por defecto “ward”.

  • .fit_predict(): Entrenará el modelo en los datos suministrados e inmediatamente genera el cluster asociado a cada elemento.

  • Si bien el método de Aglomeración no requiere el número de clusters a generar, Scikit-Learn lo exige de modo de poder etiquetar cada elemento.

¿Por qué no existen los métodos .fit() y .predict() por separado?

Otras implementaciones (Dendograma)

from scipy.cluster.hierarchy import dendrogram, linkage

# Genera los cálculos necesarios para construir el Histograma.
Z = linkage(X, method='single', metric="euclidean") 

# Graficar el Dendograma
plt.figure(figsize=(10, 5)) # Define el tamaño del Gráfico
plt.title('Dendograma Clustering Jerárquico') # Define un título para el dendograma
plt.xlabel('Iris Samples')
plt.ylabel('Distance')
dendrogram(Z, leaf_rotation=90., leaf_font_size=8.)
plt.show()

Principalmente este código permite graficar el Dendograma completo.

L4: Genera una instancia del Dendograma. (Sería equivalente al .fit() de Scikit-Learn).
L5-L12: Corresponde al código necesario para graficar el Dendograma.

Sugerencias

Pre-procesamientos

Es importante recordar que el clustering aglomerativo también es un Algoritmo basado en distancias, por lo tanto se ve afectado por Outliers y por Escala.

Se recomienda preprocesar los datos con:

  • Winsorizer() para eliminar Outliers.
  • StandardScaler() o MinMaxScaler() para llevar a una escala común.

Otras técnicas como merge y split, no aplican a este tipo de clustering debido a las limitaciones del algoritmo.

Variantes

En casos en los que no es posible calcular distancias debido a la presencia de datos categóricos, es posible utilizar el Gower Dissimilarity como medida de similitud.

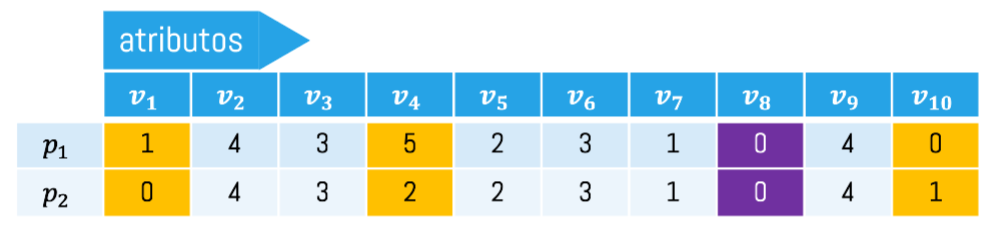
Gower
Se define como la proporción de variables que tienen distinto valor con respecto al total sin considerar donde ambos son ceros.

\[Gower(p1,p2) = \frac{3}{9}\]

C’est fini

Tics-411 Minería de Datos está licenciado bajo CC BY-NC-SA 4.0