TICS-411 Minería de Datos
Clase 7: Algoritmo Apriori
Market Basket Analysis
Introducción
Gracias a los planes de fidelización (juntar puntos, dar RUT, acumular millas, etc.) las empresas son capaces de detectar
patrones:
- Qué nos gusta,
- Qué compramos,
- Con qué frecuencia lo compramos,
- Junto con qué lo compramos
- etc.
Market Basket Analysis
Corresponde al estudio de nuestra canasta de compras. De modo que podamos entender qué cosas son las que como clientes preferimos y una empresa pueda Recomendar de manera más apropiadas.
Definiciones
- Patrón
-
Predicado (output True/False) para verificar si una estructura buscada ocurre o no.
- Tarea
-
Encontrar
reglas de asociaciónbasado en patrones.
Ejemplos
- Datasets de supermercados:
- 10% de los clientes totales compran vino y quedo (
patrón: si compro vino, también llevo queso).
- 10% de los clientes totales compran vino y quedo (
- Datasets de Alarmas:
- Si la alarma A y B suenan en un intervalo de 30 segundos, entonces la alarma C sonará dentro de un intervalo de 60 segundos con 50% de probabilidad.
Ejemplo: Datos Supermercado
- Datos Transaccionales
-
Una transacción involucra un conjunto de elementos. Una boleta de supermercado muestra el conjunto de elementos comprados por un cliente. Los productos involucrados en una transacción se denominan
items.
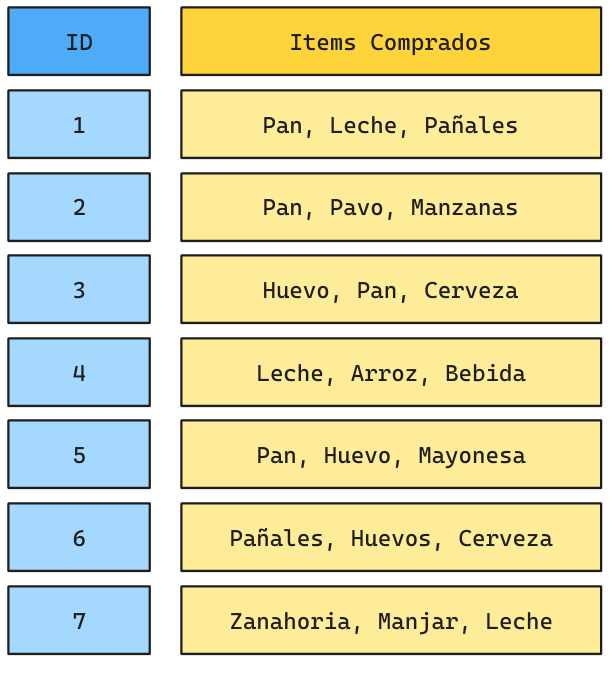
Ejemplo: Datos Supermercado
Objetivo y Aplicaciones
Objetivo
Encontrar asociaciones entre elementos u objetos de bases de datos transaccionales.
Aplicaciones
- Apoyo a toma de decisiones.
- Análisis de Información de Ventas.
- Distribución y ubicación de Mercaderías.
- Segmentación de Clientes en base de patrones de compra.
- Diágnostico y predicción de alarmas.
Definiciones: Medidas
- Support (Soporte)
- Fracción de Transacciones que contienen a \(X\). Probabilidad de que una transacción contenga a \(X\).
\[Supp(X) = P(X)\]
- Support Count
- Número de Transacciones que contienen a \(X\).
\[SuppCount(X) = Count(X)\]
- Confidence (Confianza o Eficiencia)
- Fracción de las Transacciones en las que aparece \(X\) que también incluyen \(Z\).
\[Conf(X \implies Z) = \frac{Supp(X \cup Z)}{Supp(X)}\] \[Conf(X \implies Z) = \frac{SuppCount(X \cup Z)}{SuppCount(X)}\]
Ojo con la Notación \(\cup\). En este caso significa que tanto el producto X como el Producto Z sean parte de la transacción.
Ejemplos: Support y Confidence
\[ Supp({Pan}) = 4/7\] \[ Supp({Leche}) = 3/7\] \[ Supp({Pan, Huevo}) = 2/7\]
\[ Conf({Pan} \implies {Huevo}) = \frac{Supp({Pan, Huevo})}{Supp(Pan)} = \frac{2/7}{4/7}\]
\[ Conf({Pan} \implies {Leche}) = \frac{Supp({Pan, Leche})}{Supp(Pan)} = \frac{1/7}{4/7}\] \[ Conf({Leche} \implies {Pan}) = \frac{Supp({Pan, Leche})}{Supp(Leche)} = \frac{1/7}{3/7}\]
Problema
En un dataset transaccional de n productos totales y \(|U_i|\) elementos para la Transacción \(i\).
Se pueden generar un total de \(N_{reglas}\) de asociación:
\[N_{reglas} = \sum_{i=1}^{2^{n}} \sum_{j=0}^{|U_i|}\binom{|U_i|}{j}\]
Si suponemos un supermercado que tiene 1000 productos, y transacciones que pueden ir entre 1 y 50 productos. El problema es muy costoso, y se podrían eventualmente generar demasiadas combinaciones.
Algoritmo Apriori
- Apriori
-
Es un algoritmo para aprender reglas de asociación que utiliza el principio
Aprioripara buscar de forma eficiente las reglas que satisfacen los límites de soporte y confianza.
Algoritmo
- Fijar \(k=1\) y determinar lista de candidatos de tamaño \(k\).
- Calcular la frecuencia del conjunto.
- Eliminar conjuntos con baja frecuencia (utilizando un
umbral de soporte). - Unir los conjuntos frecuentes para generar conjuntos de tamaño \(k+1\).
- Si existe la posibilidad de seguir creando combinaciones volver al
paso ay repetir.
- Usar todos los conjuntos frecuentes para generar reglas.
Ejemplo Apriori
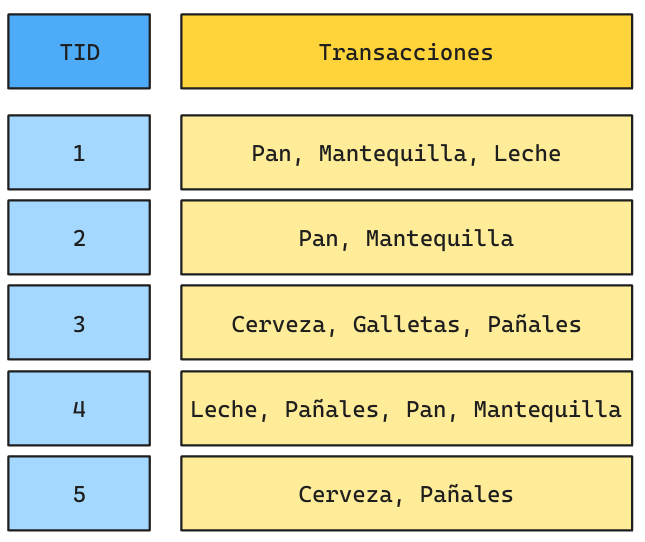
Supongamos el siguiente dataset transaccional:
Supongamos que queremos calcular las reglas de asociación que tengan un MinSupp=40% y un MinConf=70%.
Podríamos pensar que MinSupp y MinConf son los hiperparámetros de este algoritmo.
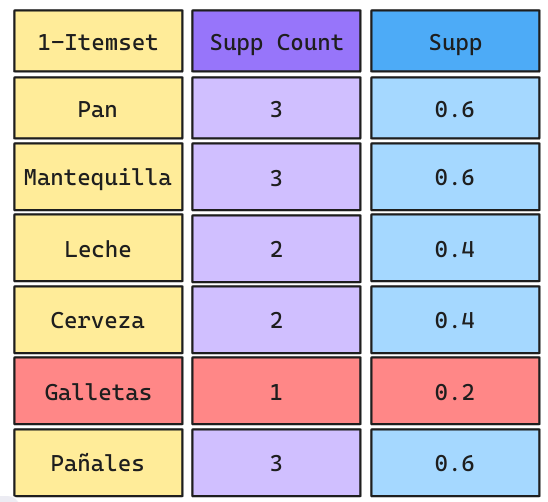
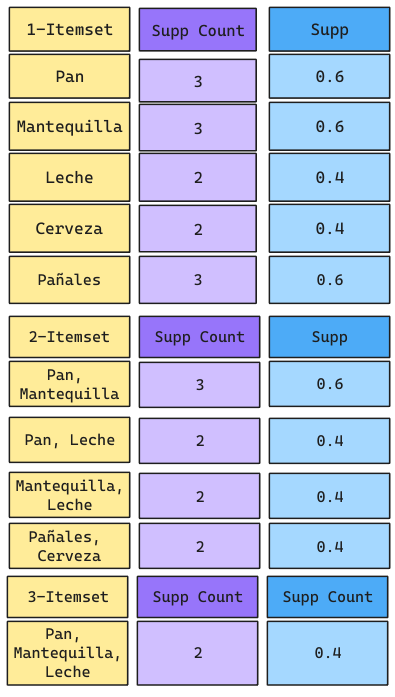
Ejemplo Apriori: Iteración 1
Galletas NO CUMPLE con el Soporte Mínimo solicitado. Por lo tanto, lo elimino y genero relaciones de 2 productos sin considerar Galletas.
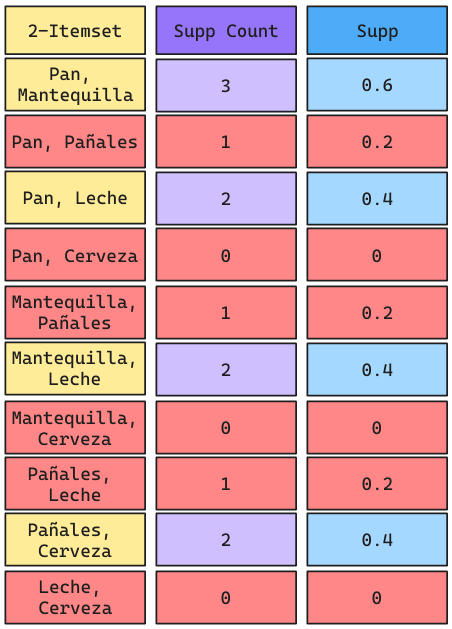
Ejemplo Apriori: Iteración 2
Acá NO SE ELIMINA ningún producto, ya que en los itemsets que sobrevivieron hay Pan, Mantequilla, Leche, Pañales y Cerveza.
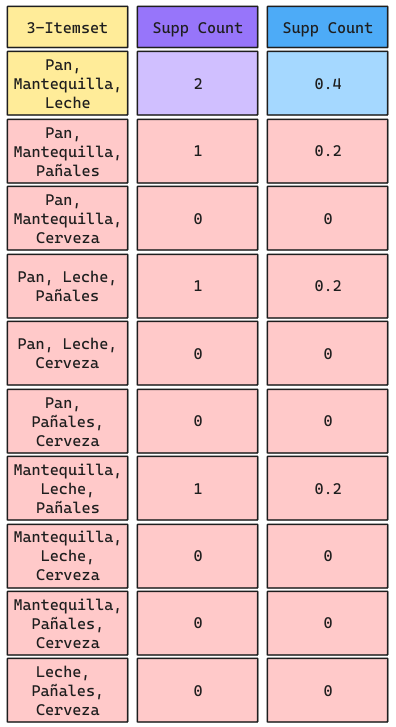
Ejemplo Apriori: Iteración 3
Se puede apreciar que los únicos 3 productos que sobreviven son Pan, Mantequilla y Leche. Por lo tanto, NO ES POSIBLE generar reglas con 4 productos.
Ejemplo Apriori: Generación de Reglas
- Para
{Pan, Mantequilla}:
\(Conf(Pan \implies Mantequilla) = \frac{Supp(Pan, Mantequilla)}{Supp(Pan)} = \frac{3}{3}\)✅ \(Conf(Mantequilla \implies Pan) = \frac{Supp(Pan, Mantequilla)}{Supp(Mantequilla)} = \frac{3}{3}\)✅
- Para
{Pan, Leche}:
\(Conf(Pan \implies Leche) = \frac{Supp(Pan, Leche)}{Supp(Pan)} = \frac{2}{3}\) ❌ \(Conf(Leche \implies Pan) = \frac{Supp(Pan, Leche)}{Supp(Leche)} = \frac{2}{2}\) ✅
- Para
{Mantequilla, Leche}:
\(Conf(Mantequilla \implies Leche) = \frac{Supp(Mantequilla, Leche)}{Supp(Mantequilla)} = \frac{2}{3}\) ❌ \(Conf(Leche \implies Mantequilla) = \frac{Supp(Mantequilla, Leche)}{Supp(Leche)} = \frac{2}{2}\) ✅
Ejemplo Apriori: Generación de Reglas
- Para
{Pañales, Cerveza}:
\(Conf(Pañales \implies Cerveza) = \frac{Supp(Pañales, Cerveza)}{Supp(Pañales)} = \frac{2}{3}\)❌ \(Conf(Cerveza \implies Pañales) = \frac{Supp(Pañales, Cerveza)}{Supp(Cerveza)} = \frac{2}{2}\)✅
- Para
{Pan, Mantequilla, Leche}:
\(Conf({Pan, Mantequilla} \implies {Leche}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Pan, Mantequilla)} = \frac{2}{3}\)❌ \(Conf({Pan, Leche} \implies {Mantequilla}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Pan, Leche)} = \frac{2}{2}\)✅ \(Conf({Mantequilla, Leche} \implies {Pan}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Mantequilla, Leche)} = \frac{2}{2}\)✅
\(Conf({Leche} \implies {Pan, Mantequilla}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Leche)} = \frac{2}{2}\)✅ \(Conf({Mantequilla} \implies {Pan, Leche}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Mantequilla)} = \frac{2}{3}\)❌ \(Conf({Pan} \implies {Mantequilla, Leche}) = \frac{Supp(Pan, Mantequilla, Leche)}{Supp(Pan)} = \frac{2}{3}\)❌
Resultado Final
Itemset MinSupp = 40%
Reglas Finales MinConf = 70%
\[Pan \implies Mantequilla\] \[Mantequilla \implies Pan\] \[Leche \implies Pan\] \[Leche \implies Mantequilla\] \[Cerveza \implies Pañales\] \[\{Pan, Leche\} \implies Mantequilla\]
\[\{Mantequilla, Leche\} \implies Pan\] \[Leche \implies \{Pan, Mantequilla\}\]
Insights:
- El Pan, la Leche y la Mantequilla están relacionados.
- Parece ser que si llevo Cervezas también llevo Pañales.
Evaluación de Reglas de Asociación
- Lift
- Mide qué tan lejos de la independencia están \(X\) e \(Y\). Lift varía entre 0 y \(\infty\).
\[Lift(X,Y) = \frac{Conf(X \implies Y)}{s(Y)}\]
- \(Lift(X,Y) \sim 1\) implica independencia y la regla no es importante.
- \(Lift(X,Y) < 1\) implica una asociación negativa de la regla.
- \(Lift(X,Y) > 1\) implica una asociativa de la regla. Un mayor Lift implica que la regla es potencialmente útil para el futuro.
Ejemplo:
\[Lift(Cerveza, Pañales) = \frac{Conf(Cerveza \implies Pañales)}{Supp(Pañales)} = \frac{1}{0.6} = 1.67\]
Una persona que compra Cerveza tiene 1.67 más chances de comprar Pañales.
Implementación en Python: Preprocesamiento
Pre-procesamiento
import pandas as pd from mlxtend.preprocessing import TransactionEncoder tre = TransactionEncoder() df = tre.fit_transform(transactions) df_encoded = pd.DataFrame(df, columns = tre.columns_)import pandas as pd from mlxtend.preprocessing import TransactionEncoder tre = TransactionEncoder() df = tre.fit_transform(transactions) df_encoded = pd.DataFrame(df, columns = tre.columns_)import pandas as pd from mlxtend.preprocessing import TransactionEncoder tre = TransactionEncoder() df = tre.fit_transform(transactions) df_encoded = pd.DataFrame(df, columns = tre.columns_)import pandas as pd from mlxtend.preprocessing import TransactionEncoder tre = TransactionEncoder() df = tre.fit_transform(transactions) df_encoded = pd.DataFrame(df, columns = tre.columns_)import pandas as pd from mlxtend.preprocessing import TransactionEncoder tre = TransactionEncoder() df = tre.fit_transform(transactions) df_encoded = pd.DataFrame(df, columns = tre.columns_)
L4: transactions debe ser una lista de listas. Cada fila, son distintas transacciones. Cada transaccion puede tener distinto número de elementos. L5: tre.columns_ extrae los nombres de los productos para que el DataFrame sea más entendible.
df_encoded es un DataFrame tipo OneHotEncoder pero con valores Booleanos (Esto es solicitado por la documentación).
Implementación en Python: Itemsets
from mlxtend.frequent_patterns import apriori itemset = apriori(df_encoded, min_support=0.5, use_colnames = True)from mlxtend.frequent_patterns import apriori itemset = apriori(df_encoded, min_support=0.5, use_colnames = True)from mlxtend.frequent_patterns import apriori itemset = apriori(df_encoded, min_support=0.5, use_colnames = True)from mlxtend.frequent_patterns import apriori itemset = apriori(df_encoded, min_support=0.5, use_colnames = True)
L3: df_encoded es el DataFrame preprocesado.
min_support: Corresponde al Soporte Mínimo para generar itemsets. Por defecto 0.5.
use_colnames: Permite que las reglas usen los nombres de las columnas para referirse a los productos. Por defecto es
False, pero conviene usarlo comoTrue.itemset será un DataFrame con los itemsets generados.
Implementación en Python: Reglas
from mlxtend.frequent_patterns import association_rules rules = association_rules(itemsets, metric="confidence", min_threshold=0.8)from mlxtend.frequent_patterns import association_rules rules = association_rules(itemsets, metric="confidence", min_threshold=0.8)from mlxtend.frequent_patterns import association_rules rules = association_rules(itemsets, metric="confidence", min_threshold=0.8)from mlxtend.frequent_patterns import association_rules rules = association_rules(itemsets, metric="confidence", min_threshold=0.8)
L3: itemset es el dataframe generado en el paso anterior.
metric: Métrica para definir reglas, puede ser “confidence” y otras definidas acá
min_threshold: Corresponde al umbral de la métrica a utilizar. Por defecto 0.8.
rules corresponde a un Dataset que tiene las Reglas de Asociación detectadas y muchas métricas asociadas.
¡Felicitaciones! 🎉🎉🎉🎉 Aprendimos Apriori!!
