TICS-579-Deep Learning

Clase 1: Introducción a los Shallow Models

Alfonso Tobar-Arancibia

alfonso.tobar.a@edu.uai.cl

Shallow Models

Modelo Básico de Clasificación Binaria

Supongamos el siguiente problema de clasificación binaria:

Sea \(\mathcal{y} \sim \text{Bernoulli}(p)\), es decir:

\[P(y) = \begin{cases} p, & \text{si y = 1} \\ 1-p, & \text{si y=0} \end{cases} \]

Pero Ojo 👀

¿Cómo estimamos la probabilidad \(p\) para asignar una clase?

• Esta clase puede ser cualquier cosa, por ejemplo, si un correo es spam o no, si es un gato o u perro, etc.

Regresión Lineal

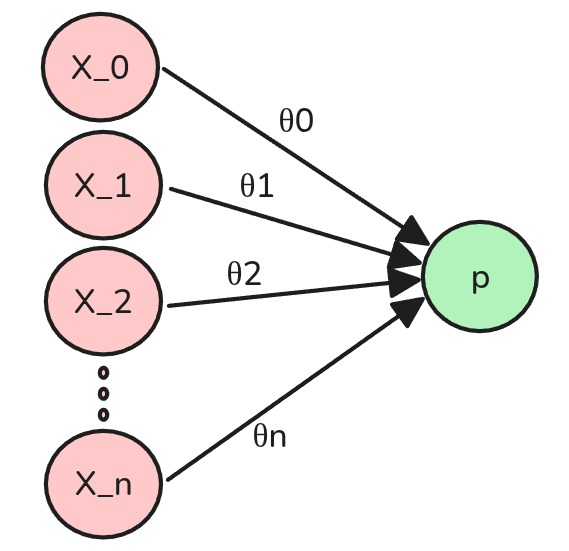
Una manera es utilizar una combinación lineal de features (inputs) y parámetros (pesos). Es decir:

\[\hat{y} = \theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n\]

Modelo Básico de Clasificación Binaria

Pero tenemos el problema de que \(y\) puede tomar cualquier valor real (no está acotada), y necesitamos que \(p\) esté entre 0 y 1. Para ello podemos aplicar la función Logística o Sigmoide.

👍 Propiedades de la función Sigmoide

• Acotada entre 0 y 1.
• Punto de Inflexión en \(x=0\), lo que se transforma en \(p=0.5\).
• \(\sigma(z)'= \sigma(z)(1-\sigma(z))\).

Estimación de la probabilidad

\[ p = \sigma(\hat{y}) = \sigma(\theta_0 x_1 + \theta_1 x_1 + ... + \theta_n x_n)\]

donde \(\sigma(x) = \frac{1}{1 + e^{-x}}\) es la función sigmoide.

Modelo Básico de Clasificación Binaria

🤓 Más definiciones

• Llamaremos parámetros a los valores \(\theta_j\), \(j=0,...,n\).
• Llamaremos “Capas” a un conjunto de parámetros utilizado para generar un resultado.

🤓 Definiciones

• Definiremos \((\bar{x}^{(i)})^T = (x_1^{(i)}, x_2^{(i)}, ..., x_n^{(i)})\) como el vector de features del punto \(i\).
• Asimismo \(y^{(i)}\) será el label/etiqueta del punto \(i\).
• En este caso particular \(m=3\) observaciones y \(n=2\) features.

Redes Neuronales

El término Red Neuronal es un término marketero, lo único que hace es mostrar de manera gráfica lo que nosotros acabamos de definir.

Red Neuronal Básica: Regresión Logística

Finalmente, por conveniencia, podemos escribir nuestra Regresión Logísitca en notación matricial:

Una observación

\[p^{(i)} = \sigma((\bar{x}^{(i)})^T \cdot \theta)\]

Muchas Observaciones

\[\bar{p} = \sigma(X \cdot \theta)\]

Donde X es el la Matriz de Diseño/Design Matrix, que contiene todos los vectores de features. Además utilizaremos la definición inicial, en la que si \(p\ge 0.5\) entonces \(y=1\) y si \(p < 0.5\) entonces \(y=0\).

Los Ingredientes de un Algoritmo de Aprendizaje

Hipótesis

Una función que describe como mapear inputs (features) con outputs (labels) por medio de parámetros. En nuestro caso inicial diremos que \(h_\theta(X) = \sigma(X \theta)\), donde \(\sigma\) es la función sigmoide.

Loss Function

Una función que especifica cuanta información se pierde. Mayor pérdida implica más error de estimación.

Método de Optimización

Es el responsable de combinar la hipótesis y la loss function. Corresponde a un procedimiento para determinar los parámetros de la hipótesis, minimizando la suma de las pérdidas en un set de entrenamiento.

Regresión Logística: Loss Function

Nuestra definición inicial de la Distribución Bernoulli puede ser rescrita de la siguiente manera:

\[P(y) = \begin{cases} p, & \text{si y = 1} \\ 1-p, & \text{si y=0} \end{cases} \]

\[P(y|X) = p^{y} (1-p)^{1-y}\]

Maximum Likelihood Estimation

Permite calcular los parámetros \(\theta\) que maximizan la probabilidad de observar los datos (que los datos se ajusten a la distribución esperada por el modelo).

\[\mathcal{L}(\theta) = \prod_{i=1}^m P(y^{(i)}|X^{(i)}) = \prod_{i=1}^m p^{y^{(i)}} (1-p)^{1-y^{(i)}}\]

Negative Log Likelihood

• La Productoria no es amigable.
• Es más común minimizar que maximizar.
• Aplicamos Logaritmo a la función de verosimilitud y cambiamos el signo.

\[\mathcal{l}(\theta) = -\log(\mathcal{L}(\theta)) = -\sum_{i=1}^m \left(y^{(i)} \log(p^{(i)}) + (1-y^{(i)}) \log(1-p^{(i)})\right)\]

Regresión Logística: Loss Function

Función de Pérdida/Loss Function en notación matricial

\[L(\theta) = -\frac{1}{m}\left[y^T \log(\bar{p}) + (1-y)^T \log(1-\bar{p})\right]\]

donde \(\bar{p} = \sigma(X\theta)\) es el vector de probabilidades estimadas por el modelo.

• Atención: Es más común calcular la pérdida promedio, es decir, dividir por \(m\).

Propiedades

• Si \(y^{(i)} = 1\), entonces \(L(\theta) = -\frac{1}{m}log(p^{(i)})\).
  • Luego si la probabilidad es cercana a 1, que significa que el modelo predijo correctamente la clase, entonces la pérdida es cercana a 0.
  • Pero si la probabilidad es cercana a 0, entonces la pérdida es alta.
• Si \(y^{(i)} = 0\), entonces \(L(\theta) = -\frac{1}{m}log(1-p^{(i)})\).
  • Luego si la probabilidad es cercana a 0, que significa que el modelo predijo correctamente la clase, entonces la pérdida es cercana a 0.
  • Pero si la probabilidad es cercana a 1, entonces la pérdida es alta.

Conclusión

• La Función de Pérdida mide cuánta información se pierde al estimar los parámetros \(\theta\). En otras palabras, mide el error de estimación de nuestro modelo. Por lo tanto, una Loss Function más baja implica un mejor modelo.

• Si minimizamos nuestra función de pérdida, entonces estamos maximizando la probabilidad de observar los datos. Por lo tanto, minimizamos el error de estimación del modelo.

• A veces está ecuación aparece como la pérdida promedio (es decir, está multiplicada por \(\frac{1}{m}\)).

Regresión Logística: Método de Optimización

🤘 La parámetros óptimos del problema están dados por:

\[\underset{\theta}{argmin} = L(\theta)\]

• Lo cuál puede ser resuelto fácilmente utilizando un método de optimización como el Gradient Descent.

Parámetros óptimos se encuentran con:

\[\theta = \theta - \alpha \nabla_\theta L(\theta)\]

😇 ¿Cuánto vale el gradiente de la Función de Pérdida?

Vamos a calcular el gradiente haciendo trampa. Puede que algunos se enojen, pero para nosotros es suficiente.

Regresión Logísitca: Gradiente

Supongamos lo siguiente:

• \(a= X \theta\)
• \(b = \sigma(a)\)
• \(c = log(b)\)
• \(d = log(1-b)\)
• \(e = y^T c\)
• \(f = (1-y)^T d\)
• \(L* = e + f\)
• \(L = -\frac{1}{m} L*\)

Regresión Logísitca: Calculando el Gradiente

\[ \begin{align*} \frac{\partial L*}{\partial f} &= \frac{\partial L}{\partial e} = 1 \\ \frac{\partial L*}{\partial d} &= \frac{\partial L}{\partial f} \cdot \frac{\partial f}{\partial d} = (1 - y)^T \\ \frac{\partial L*}{\partial c} &= \frac{\partial L}{\partial e} \cdot \frac{\partial e}{\partial c} = y^T \\ \frac{\partial L*}{\partial b} &= \frac{\partial L}{\partial c} \cdot \frac{\partial c}{\partial b} + \frac{\partial L}{\partial d} \cdot \frac{\partial d}{\partial b}= \frac{y^T}{b} - \frac{(1-y)^T}{1-b} \\ \frac{\partial L*}{\partial a} &= \frac{\partial L}{\partial b} \cdot \frac{\partial b}{\partial a} = \left[\frac{y^T}{b} - \frac{(1-y)^T}{1-b}\right] \cdot \sigma(a)' \\ \frac{\partial L*}{\partial \theta} &= \frac{\partial L}{\partial a} \cdot \frac{\partial a}{\partial \theta} = \left[\frac{y^T}{b} - \frac{(1-y)^T}{1-b}\right] \cdot \sigma(a)' \cdot X\\ \frac{\partial L*}{\partial \theta} &=\left[\frac{y^T (1-b) + b (1-y)^T}{b(1-b)}\right] \cdot \sigma(a)' \cdot X\\ \frac{\partial L*}{\partial \theta} &=\left[\frac{y^T - b}{b(1-b)}\right] \cdot \sigma(a)' \cdot X\\ \end{align*} \]

Regresión Logísitca: Gradiente

\[\frac{\partial L*}{\partial \theta} =\left[\frac{y^T - b}{b(1-b)}\right] \cdot \sigma(a)' \cdot X\]

Luego reemplazamos que \(b=\sigma(a)\) y \(\sigma(a)'=\sigma(a)(1-\sigma(a))\):

Obtenemos que:

\[\frac{\partial L}{\partial \theta} = \frac{1}{m}\left[\sigma(X\theta)_{m \times 1} - y^T_{1 \times m}\right]X_{m \times (n+1)}\]

😅Ojo con las dimensiones.

Debemos modificar nuestro cálculo de modo que las dimensiones sean compatibles. Luego:

\[\frac{\partial L}{\partial \theta}_{(n+1) \times 1} = \frac{1}{m} X^T_{(n+1) \times m} \cdot \left[\sigma(X\theta) - y\right]_{m \times 1}\]

• Tengo que tener un gradiente para cada parámetro (¿por qué son \(n+1\)?)

Regresión Logística: Update Rule

Llamaremos Update Rule al Algoritmo que permite entrenar un modelo. En el caso de la Regresión Logística, el Update Rule es:

\[\theta_{n+1 \times 1} = \theta_{n+1 \times 1} - \frac{\alpha}{m} \cdot X^T_{(n+1) \times m} \cdot \left[\sigma(X\theta) - y\right]_{m \times 1}\]

🤫 Resumen

• Aplicando este procedimiento es posible definir cualquier update rule de aprendizaje supervisado. Tan sólo se requiere:

• Una Hipótesis: En el caso de la Regresión Logística es \(h_{\theta}(X) = \sigma(X \theta)\).

• Una Loss Function: En el caso de la regresión Logística es \(L(\theta) = -\left[y^T \log(h_{\theta}) + (1-y)^T \log(1-h_\theta)\right]\)

• Encontrar los gradientes de la Loss Function.

😱Entrenamiento

• Llamaremos al proceso de encontrar los parámetros óptimos del modelo “Entrenamiento”. Es decir, el proceso de encontrar los parámetros \(\theta\) que minimizan la Loss Function \(L(\theta)\).
• Un modelo que ya está entrenado, puede ser utilizado para hacer predicciones en nuevos datos. Es fin último de un modelo de Machine Learning es utilizarse en producción, no sólo presentar métricas.

🤯