TICS-579-Deep Learning
Clase 2: Introducción a las Redes Neuronales
¿Por qué Machine Learning y Deep Learning no son lo mismo?
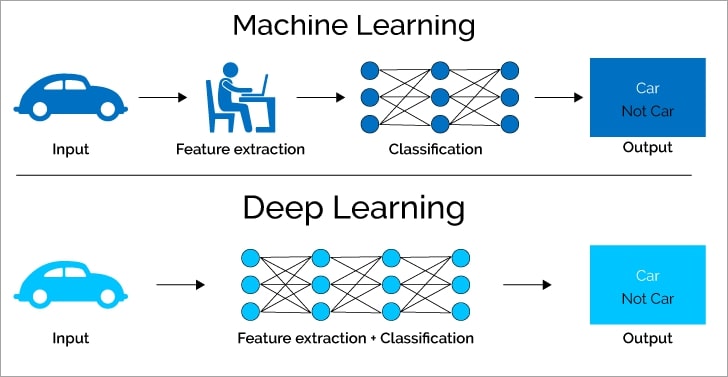
Machine Learning vs Deep Learning
Es sabido que la mejor manera de mejorar el performance de un algoritmo en partícular no es con ajuste de Hiperparámetros sino crear features que sean representativas del problema.
🤓 ¿Cómo se mejora un modelo?
- Normalmente el
Machine Learningbusca generar features de manera manual. Deep Learningbusca que el Algoritmo genere esas features de manera automática.
¿Cómo se crean features?
Normalmente un approach es agregar features externas/exógenas, pero también es completamente válido crear features nuevas por medio de las existentes.
Ejemplo
Si \(X_1\) es el Largo de un objeto y \(X_2\) es el ancho, entonces una feature nueva podría ser \(X_3 = X_1 \cdot X_2\), que es el área del objeto.
¿Cómo podríamos crear nuevas features pero de manera automática?
- Una opción es hacer una combinación lineal de features existentes.
Esto lo podemos realizar con operaciones matriciales.
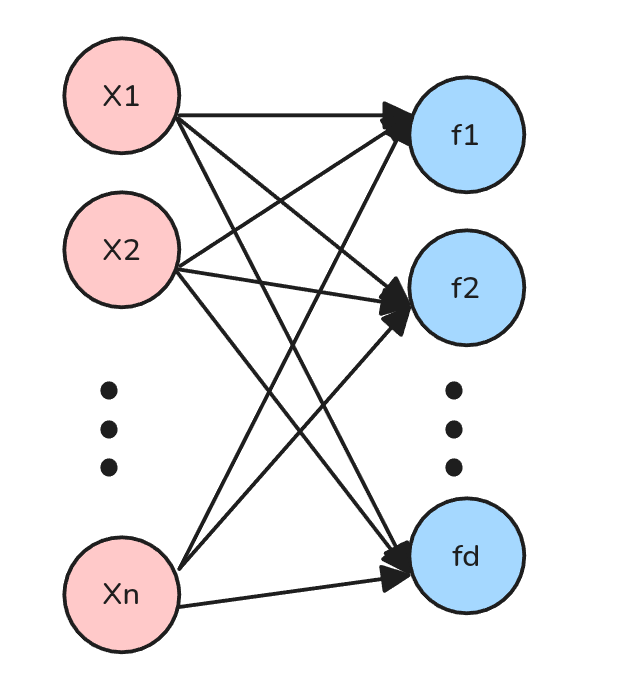
Por ejemplo un set de nuevas features \(\phi(X)\) podría ser:
\(\phi(X) = X W\) donde \(W \in \mathbb{R}^{n \times d}\), donde \(d\) es el número de nuevas features resultantes luego del proceso de creación.
- Esto implica que si \(X\) tiene \(n\) features, entonces \(\phi(X)\) tendrá \(d\) features que son combinaciones de las anteriores.
Regresión Logística + Features
😱 ¿Y si combinamos ambas ideas?
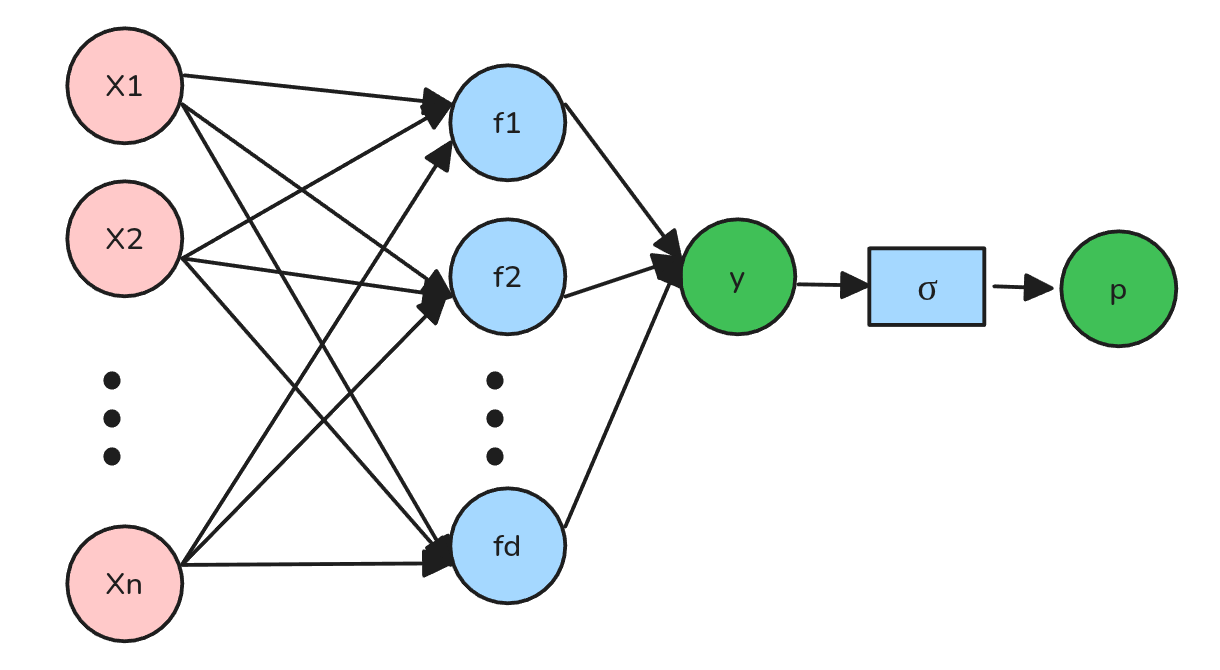
Perfectamente podemos crear una Regresión logística con nuestras nuevas features y combinar todo en un sólo modelo:
\[h_\theta(X) = p = \sigma(\phi(X) \theta) = \sigma(X W \theta)\]
🤓 Nuestra Notación
- Cada nodo se le conoce como Neurona o
Activación. - Cada conjunto de vértices, se les conoce como
CapaoCapa de Parámetros.- Ojo: Las capas no son los conjuntos de Nodos.
👀 Ojo
- Existen convenciones donde cada conjunto de nodos es una capa.
- A la primera capa de nodos se le llama Capa de
Entrada/Input Layer. - A la última capa de nodos se le llama Capa de
Salida/Output Layer. - A las capas intermedias se les llama
Hidden Layers.
- A la primera capa de nodos se le llama Capa de
¿Y si hacemos nuestro modelo más profundo?
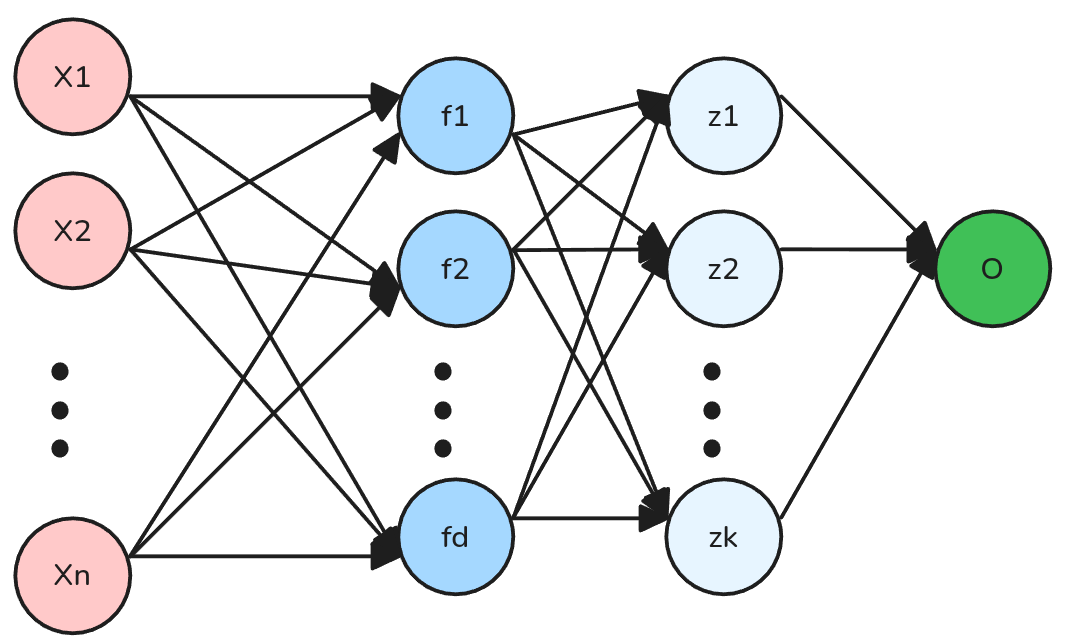
Podemos hacer nuestro modelo más profundo, agregando más capas de features. Por ejemplo:
\[h_\theta(X) = \sigma(X W_1 W_2 \theta)\]
Donde \(X \in \mathbb{R}^{m \times n}\), \(W_1 \in \mathbb{R}^{n \times d}\), \(W_2 \in \mathbb{R}^{d \times k}\) y \(\theta \in \mathbb{R}^{k \times 1}\).
🤔 El problema
Lamentablemente agregar capas no soluciona el problema de la linealidad. Agregar muchas capas lineales siguen siendo una transformación lineal.
\[ h_\theta(X) = \sigma(X W_1 W_2 \theta) = \sigma(X \tilde{\theta})\]
Donde \(\tilde{\theta} \in \mathbb{R}^{n \times 1}\) es sólo otra matriz de parámetros.
Atención: En este caso \(\sigma(\cdot)\) tiene como único propósito acotar la salida entre 0 y 1.
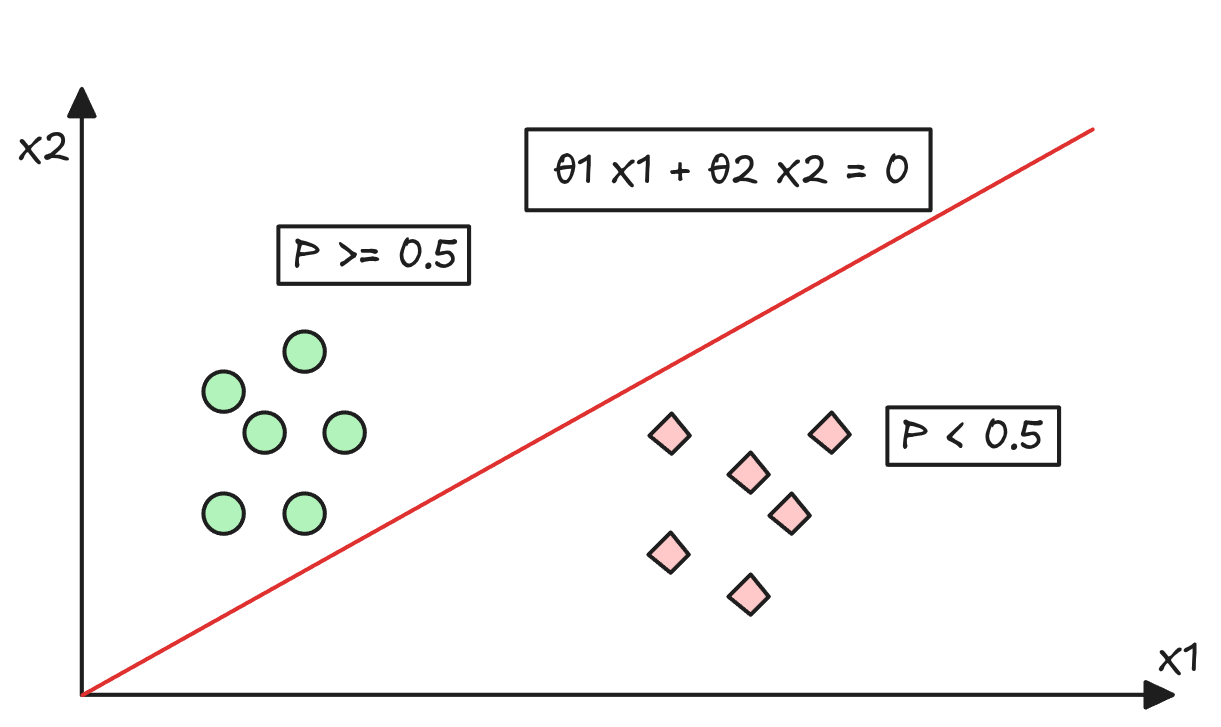
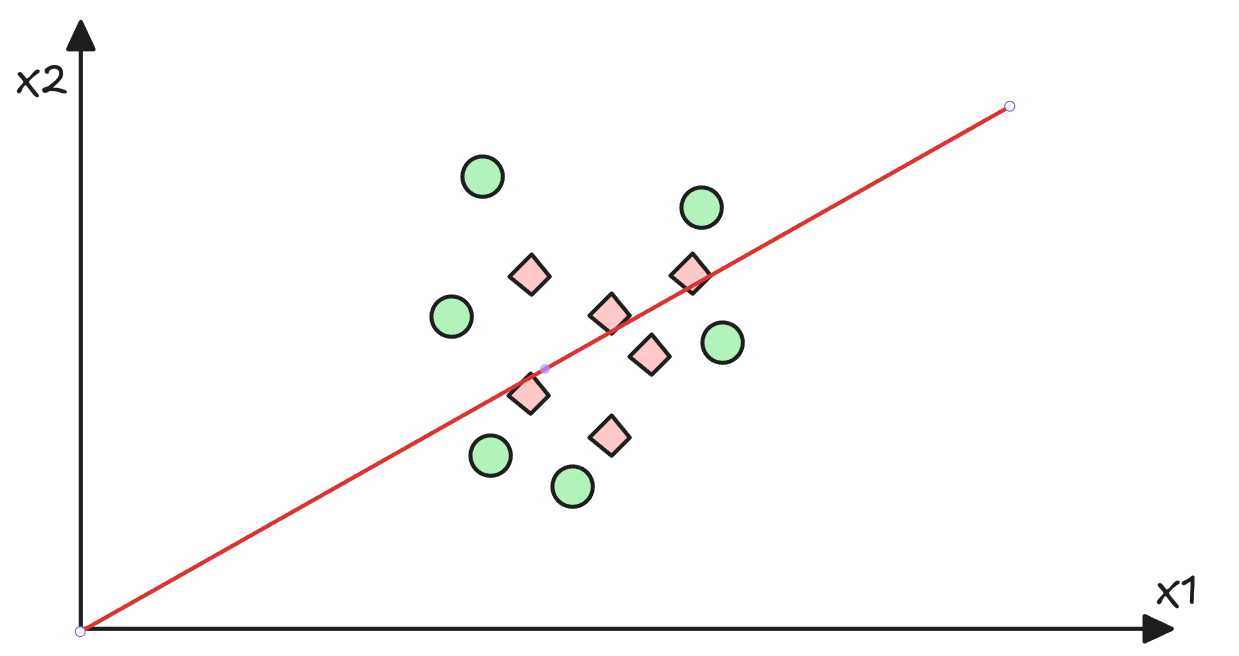
El problema de una Hipótesis Lineal
😞 No podemos salir del Origen
Por definición de una transformación lineal, si \(X=0\) entonces \(h_\theta(X)=0\). Eso lamentablemente limita las posibilidades de un modelo de poder generar una buena separación entre clases.
¿Entonces cómo solucionamos este problema?
Haremos una transformación Affine. Es decir, agregaremos un bias a nuestra transformación lineal.
\[\phi_{L+1}(X) = \phi_L(X) W_{L+1} + b_{L+1}^T\]
- Donde:
- Donde \(\phi(X)_{L+1}\) corresponde a las activaciones de la capa \(L+1\). \(L=0,...,L_{net}-1\).
- Notar que \(\phi_0(X) = X\).
- Asimismo, \(\phi_{L_{net}}(X)\) corresponde a las activaciones de la capa de salida, es decir, las predicciones del modelo.
- \(W_{L+1}\) es la matrix de
pesos/parámetrosque lleva de \(n_L\) a \(n_{L+1}\) dimensiones. - \(b_{L+1}^T\in \mathbb{R}^{1 \times n_{L+1}}\) es el vector de
biasde la capa \(L\) (Esto no es un error).
- Donde \(\phi(X)_{L+1}\) corresponde a las activaciones de la capa \(L+1\). \(L=0,...,L_{net}-1\).
¡Pero esto es una operación inválida! 🙄 No. Gracias al Broadcasting, esto es equivalente a hacer \(1_m \bar{b}^T\), donde \(1_m\) es un vector columna de unos de tamaño \(m x 1\) Esto implica que cada componente de \(\bar{b}\) se suma igual a todas las muestras.
Tip
Vamos a utilizar funciones no lineales. Cualquiera sirve tal que:
\[\phi_{L+1}(X) = \sigma_{L+1}(\phi_L(X) W_{L+1} + b_{L+1}^T)\]
- Donde \(\sigma_{L+1}\) es una función no lineal que aplica a cada elemento de la matriz \(X W_{L+1} + b_{L+1}^T\).
- \(\sigma_{L+1}\) puede ser cualquier función no lineal, pero normalmente utilizamos funciones diferenciables.
Formalmente: Una Red Neuronal Profunda
Vamos a definir una Red Neuronal Profunda como:
\[h_\theta(X) = \sigma_{L+1}(\phi_L(X) W_{L+1} + b_{L+1}^T)\]
con \(L=0,...,L_{net}-1\).
Importante
- \(L_{net}\) es el número de capas de parámetros ocultas de la red neuronal.
- Notar que \(\phi_0(X) = X\).
- Existen \(L_{net} + 1\) capas de activación. Una que es la capa de entrada \(\phi_0(X)\) y \(L_{net}\) capas “calculadas”.
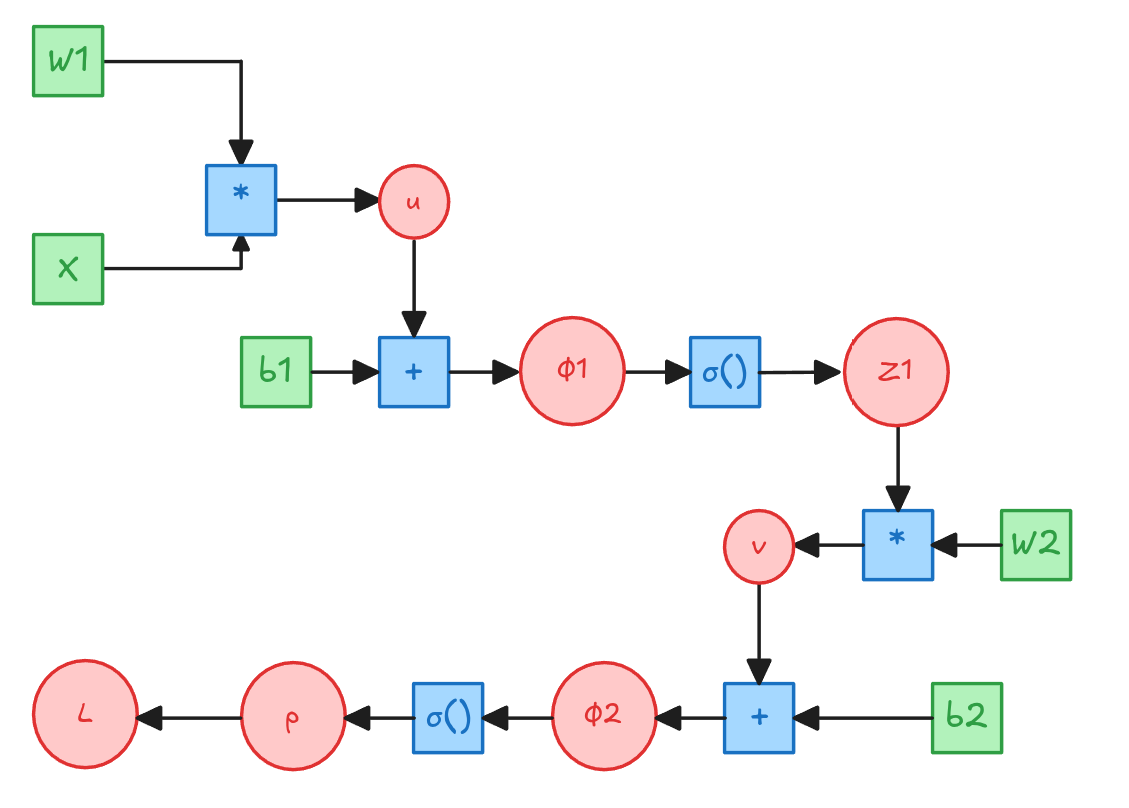
Entrenemos una Red Neuronal a mano
\(W_1 \in \mathbb{R}^{n \times d1}\)
\(\bar{b_1}^T \in \mathbb{R}^{1 \times d1}\)
\(W_2 \in \mathbb{R}^{d1 \times d2}\)
\(\bar{b_2}^T \in \mathbb{R}^{1 \times d2}\)
\[u=X W_1\] \[\phi_1 = u + 1_m\bar{b_1}^T\] \[Z_1 = \sigma(\phi_1)\] \[v=Z_1 W_2\] \[\phi_2 = v + 1_m\bar{b_2}^T\] \[p = \sigma(\phi_2)\] \[L = -\frac{1}{m}\left[y^T log(p) + (1-y)^T log(1-p)\right]\]
Entrenemos una Red Neuronal a mano
Si \(L=-[y^T log(p) + (1-y)^T log(1-p)]\) entonces:
\[\frac{\partial L}{\partial p} = -\frac{1}{m} \left[\frac{y^T}{p} - \frac{1 -y)^T}{(1-p)}\right] = \frac{1}{m} \left[\frac{p-y}{p(1-p)}\right]\]
\[\frac{\partial L}{\partial \phi_2} = \frac{\partial L}{\partial p} \frac{\partial p}{\partial \phi_2} = \frac{1}{m} \left[\frac{p-y}{p(1-p)}\right] p (1-p) = \frac{1}{m} \left[p-y\right]\]
\[\frac{\partial L}{\partial b_2} = \frac{\partial L}{\partial \phi_2} \frac{\partial \phi_2}{\partial b_2} = \frac{1}{m} 1_m^T \left[p-y\right]\]
\[\frac{\partial L}{\partial v} = \frac{\partial L}{\partial \phi_2} \frac{\partial \phi_2}{\partial v} = \frac{\partial L}{\partial \phi_2}\]
\[\frac{\partial L}{\partial W_2} = \frac{\partial L}{\partial v} \frac{\partial v}{\partial W_2} = \frac{\partial L}{\partial v} \cdot Z_1= \frac{1}{m} Z_1^T \left[p-y\right]\]
Update Rule para \(b_2\)
\[b_2^T = b_2^T - \alpha \frac{1}{m} 1_m^T \left[p-y\right]\]
Update Rule para \(W_2\)
\[W_2 = W_2 - \alpha \frac{1}{m} Z_1^T \left[p-y\right]\]
Entrenemos una Red Neuronal a mano
\[\frac{\partial L}{\partial Z_1} =\frac{\partial L}{\partial \phi_2} \frac{\partial \phi_2}{\partial Z_1}= \frac{\partial L}{\partial \phi_2} \cdot W_2^T = \frac{1}{m}[p-y] W_2^T \]
\[\frac{\partial L}{\partial \phi_1} = \frac{\partial L}{\partial Z_1} \frac{\partial Z_1}{\partial \phi_1}= \frac{\partial L}{\partial Z_1} \cdot \sigma'(\phi_1) = \frac{1}{m}[p-y] W_2^T \odot [Z_1 \odot (1-Z_1)]\]
\[\frac{\partial L}{\partial b_1} =\frac{\partial L}{\partial \phi_1} \frac{\partial \phi_1}{\partial \phi_1}{\partial b_1}= \frac{\partial L}{\partial \phi_1} \cdot 1_m = \frac{1_m^T}{m} [p-y] W_2^T \odot [Z_1 \odot (1-Z_1)]\]
\[\frac{\partial L}{\partial u} = \frac{\partial L}{\partial \phi_1} \frac{\partial \phi_1}{\partial u} = \frac{\partial L}{\partial \phi_1}\]
\[\frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial u} \frac{\partial u}{\partial W_1} = \frac{\partial L}{\partial u} \cdot X = \frac{1}{m} X^T [p-y] W_2^T \odot [Z_1 \odot (1-Z_1)]\]
Update Rule para \(b_1\)
\[b_1^T = b_1^T - \alpha \frac{1_m^T}{m} [p-y] W_2^T \odot [Z_1 \odot (1-Z_1)]\]
Update Rule para \(W_1\)
\[W_1 = W_1 - \alpha \frac{1}{m} X^T [p-y] W_2^T \odot [Z_1 \odot (1-Z_1)]\]
Entrenamiento de una Red Neuronal
➡️ Forward Pass
- Corresponde al proceso de calcular las activaciones de cada capa para una matriz de diseño \(X\).
- El forward pass permitirá calcular las variables intermedias que son necesarias para el cálculo del
Backward Passlas cuales van variando a medida que los parámetros del modelo se actualizan.
⬅️ Backward Pass
- Corresponde al proceso de calcular las derivadas de cada una de las variables del modelo con respecto a la función de pérdida.
- Notar que muchos calculos del
Backward Passdependen de los resultados delForward Pass.
👀 Backpropagation
La combinación del Forward Pass y el Backward Pass se conoce como Backpropagation o Retropropagación.
😱 Terminamos!!
Anexo
Broadcasting Rules
Broadcasting
Corresponde a una replica de una dimensión de manera de permitir alguna operación que requiera que ciertas dimensiones calcen.
Broadcasting Rules
- Cada tensor debe tener al menos una dimensión.
- Moviéndose de derecha a izquierda por cada dimensión una vez alineadas a la derecha, las dimensiones deben:
- Ser iguales,
- iguales a 1,
- o no debe existir.
El Broadcasting evita que se tenga que almacenar información repetida, lo cual permite que las implementaciones sean más eficientes en términos de memoria. Siempre que se pueda se debe utilizar Broadcasting para simplificar un cálculo.
Más info ver: Numpy Docs