TICS-579-Deep Learning
Clase 3: Feed Forward Networks
Feed Forward Networks
Feed Forward Networks
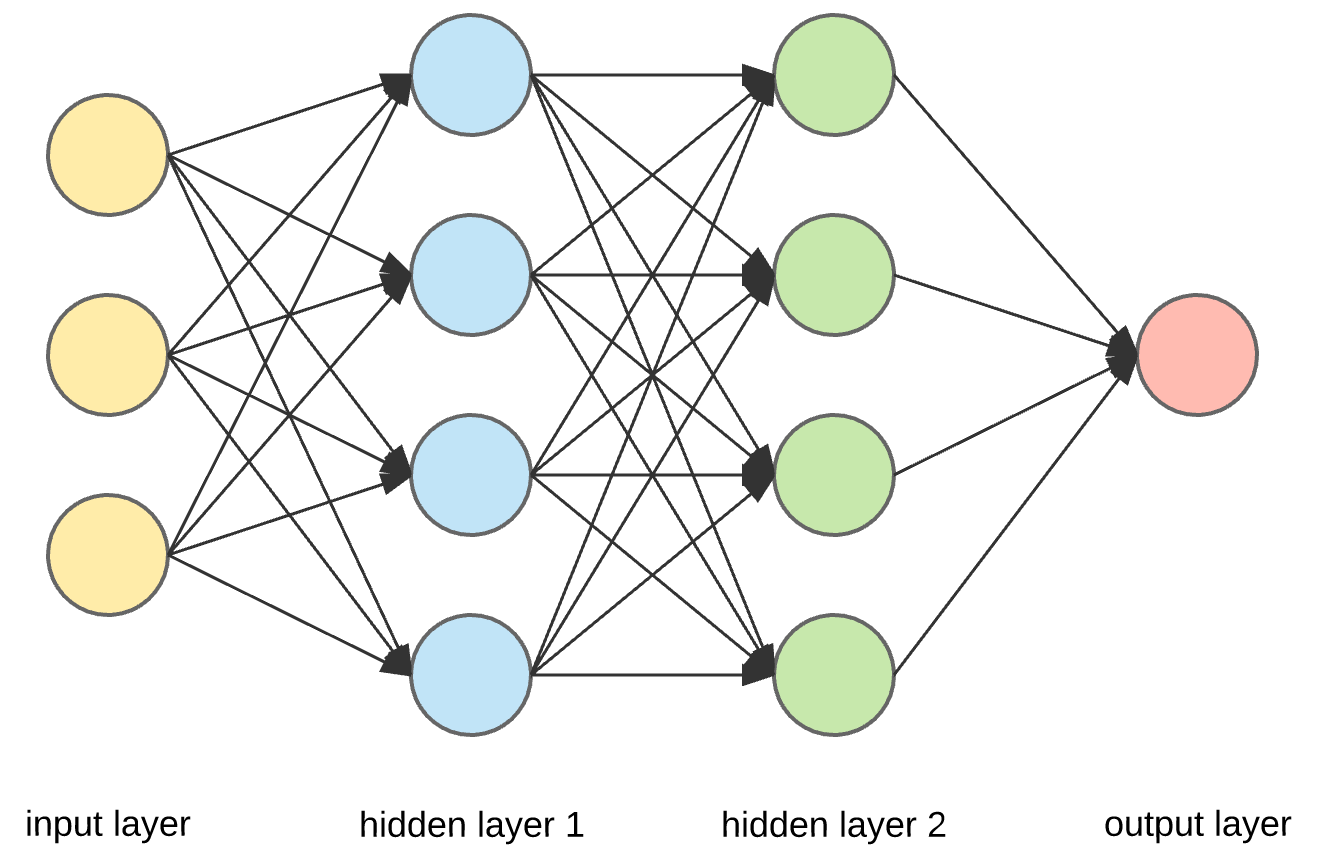
Son redes neuronales que se caracterizan por tener una arquitectura en la que la información fluye en una sola dirección, desde las entradas hasta las salidas. En general todas las neuronas de una capa están conectadas a todas las neuronas de la siguiente capa, sin ciclos ni conexiones recurrentes.
- Teorema de aproximación Universal
-
Una red neuronal feedforward con al menos una capa oculta y un número finito de neuronas, usando funciones de activación no lineales (como sigmoide, tanh o ReLU), puede aproximar cualquier función continua definida en un conjunto compacto (acotado y cerrado) de \(\mathbb{R}^n\) a cualquier nivel de precisión, siempre que se utilicen suficientes neuronas y se ajusten adecuadamente los pesos y sesgos.
Importante
- El teorema dice que es posible encontrar aproximar cualquier función.
- El teorema no dice ni cómo se hace ni los recursos necesarios para hacerlo (Número de Neuronas, capas, Hiperparámetros, etc.).
- Básicamente nos están diciendo que tienes la mejor herramienta que existe, pero es tu responsabilidad saber cómo utilizarla y qué recursos necesitas para lograrlo.
Feed Forward Networks (FFN)
Este tipo de Redes tiene distintos nombres que son usados de manera intercambiable:
- Capas Lineales: Probablemente por su denominación en Pytorch.
- Capas/Redes Densas: Probablemente por su denominación en Tensorflow.
- Multilayer Perceptron: O también conocido como MLP, debido a que es la generalización del Perceptrón, la primera propuesta de Redes Neuronales de Rosenblatt en 1958.
- Projection Layers: Probablemente por su denominación en algunos papers. Se usa en el contexto de proyectar de \(n\) dimensiones a \(d\) dimensiones.
De ahora en adelante utilizaremos las siguiente notación para referirnos a una Red Neuronal Feed Forward:
\[h_\theta(X) = \sigma_s(Z)\]
Logits
Definiremos \(Z=\phi_L(X) W_{L+1} + b_{L+1}^T\) como Logits y corresponden a las activaciones de la última capa antes de aplicar la función de activación de salida \(\sigma_s(.)\).
Hiperparámetros de una Red Neuronal
- Hiperparámetros
-
Son las configuraciones externas que no se aprenden durante el entrenamiento, sino que se definen antes de entrenar el modelo y controlan su comportamiento y rendimiento.
🤓 Hiperparámetros de una Red Neuronal
- Learning Rate (Karpathy Constant: 3e-4), valores entre [1e-5, 1e-1] son comunes.
- Número de Capas y sus respectivas dimensiones (Para Pesos/Weights y Sesgos/Biases).
- Funciones de Activación para cada capa.
- Función de Pérdida (Loss Function) a utilizar.
- Optimizador a utilizar.
- Punto de Partida de los Parámetros (Inicialización de Pesos y Sesgos).
- ¿Cuánto tiempo debo entrenar mi modelo? ¿Cómo sabemos si es que convergió o no?
Output de una Red Neuronal
En el aprendizaje supervisado se abordan principalmente dos tipos de problemas: clasificación y regresión. Según el tipo de problema, la hipótesis debe adoptar una forma distinta en la capa de salida.
⚠️ Dimensión de Salida
Está definida por el número de valores a predecir para cada observación. Denominaremos \(k\) como la dimensión de salida.
Para una red de dos capas:
\[\phi_0(X) = X\] \[\phi_1(X) = \sigma_1(W_1 \cdot \phi_0(X) + \bar{b_1}^T)\] \[\phi_2(X) = \sigma_2(W_2 \cdot \phi_1(X) + \bar{b_2}^T)\]
Donde \(W_1 \in \mathbb{R}^{n \times d_1}\) y \(W_2 \in \mathbb{R}^{d_1 \times k}\) y \(b_1 \in \mathbb{R}^{d_1}\) y \(b_2 \in \mathbb{R}^{k}\).
✅ Activación de la Salida
Según el tipo de problema, la capa de salida puede necesitar una función de activación particular que ajuste los resultados al formato correcto. En este sentido, \(\sigma_2\) estará determinada por la naturaleza del problema a resolver.
Consejos para el Output de una Red
Clasificación Binaria
El approach más común utiliza \(k=1\) con una Sigmoide para calcular la probabilidad de la clase 1. Otros approach utilizan \(k=2\) para calcular la probabilidad de ambas clases (Activando con Softmax).
Clasificación Multiclase
Utiliza \(k=C\) donde C es el número de clases a clasificar. Se usa una función Softmax para transformar el output en una distribución de probabilidades.
Clasificación Multilabel
Se requiere un \(k=C\) donde C es el número de clases a clasificar. Se usa una función Sigmoide para transformar cada clase en probabilidades.
Regresión Simple
Se requiere un \(k=1\). Típicamente no requiere de funciones adicionales aunque a veces se agregan funciones para acotar la salida.
Regresión Multiple
Se requiere un \(k=V\) con V el número de valores a predecir. Se deben tener las mismas consideraciones para acotar la salida.
👀 Muy Importante
En la mayoría de las implementaciones en Código la activación de la salida va embebida en la Loss Function. Por lo tanto, no es necesario aplicar una función de activación explícita en la capa de salida. Aunque sí deben aplicarse al momento de la Predicción del modelo.
Funciones de Activación
- Activation Functions
- Corresponden a las funciones que agregarán características no lineales a cada activación, impidiendo la composición de transformaciones Affine.
🤓 Convención para Código
En Pytorch, nunca aplicaremos una función de activación a la capa de salida.
Cuidado
Otros frameworks como Tensorflow, Keras, etc. utilizan una convención distinta y aplican funciones de activación a la capa de salida.
¿Puedo aplicar distintas Funciones de Activación a cada Neurona?
Puedo, pero no se hace. Complicaría muchísimo la implementación.
Funciones de Activación
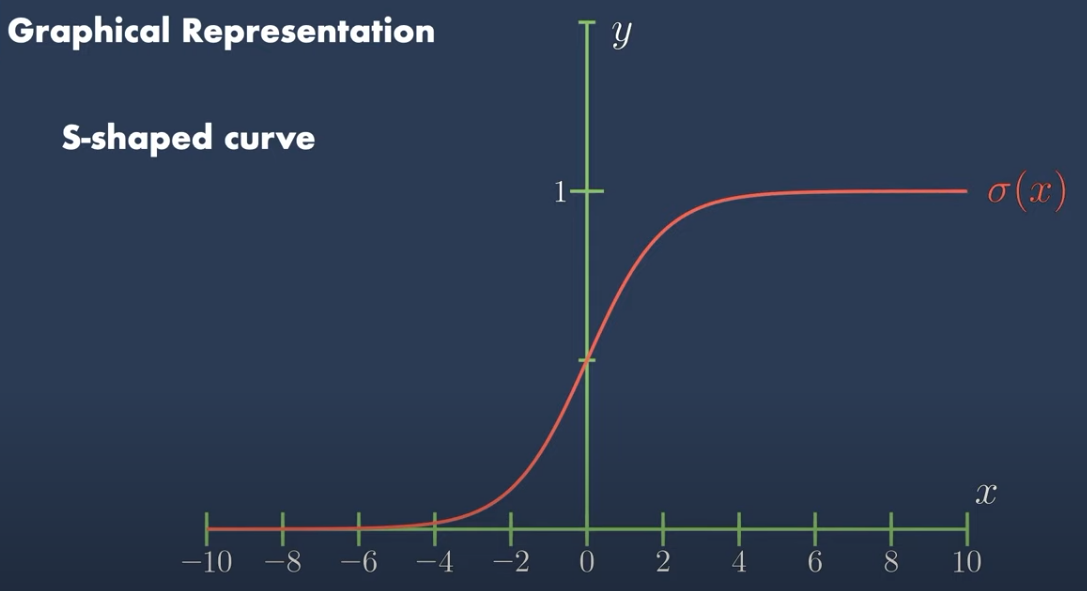
Sigmoide
Definición
\[\sigma(z) = \frac{1}{1 + e^{-z}}\]
Propiedades
- Acota la salida entre 0 y 1.
- Su derivada es \(\sigma'(z) = \sigma(z)(1 - \sigma(z))\).
- Su gradiente es general es muy pequeño, lo que lleva a problemas de Vanishing Gradient.
- Su principal uso es en la capa de salida para problemas de clasificación binaria y Clasificación Multilabel.
Funciones de Activación
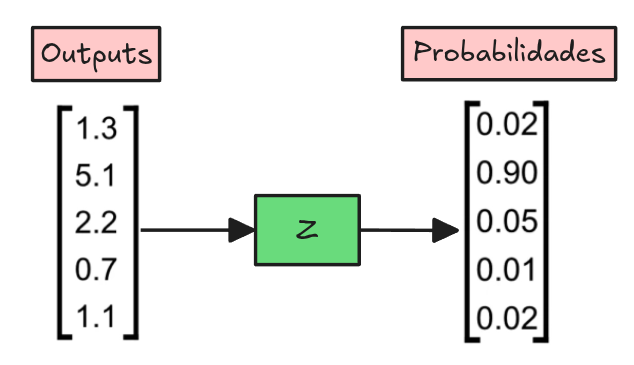
Softmax
Definición
\[S_i(z) = \frac{e^{z_i}}{\sum_{j=1}^k e^{z_j}}\]
Propiedades
- Transofrma un vector en una distribución de probabilidad.
- Su principal uso es en la capa de salida para problemas de clasificación multiclase. Es por lejos la función de activación más utilizada en la salida, pero en casos más avanzados también en Mecanismos de Atención.
Funciones de Activación
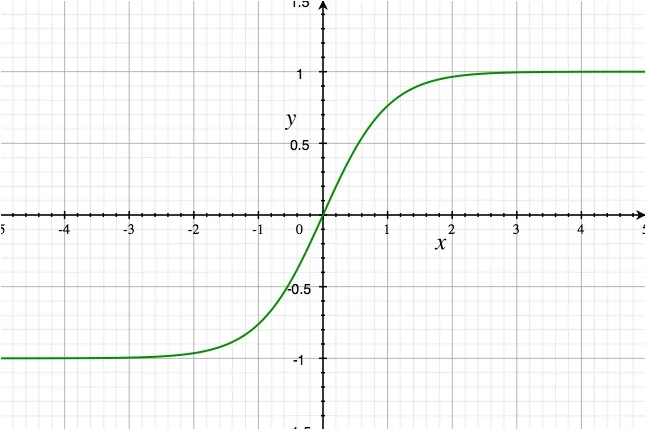
Tanh
Definición
\[Tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\]
Propiedades
- Acota su salida entre -1 y 1.
- Su derivada es \(Tanh'(z) = 1 - Tanh^2(z)\).
- Su gradiente normalmente es más grande que el de la Sigmoide, pero aún así puede llevar a problemas de Vanishing Gradient.
- A pesar de estar un poco en desuso, tiene un rol protagónico en las
Redes Recurrentes(RNNs).
Funciones de Activación
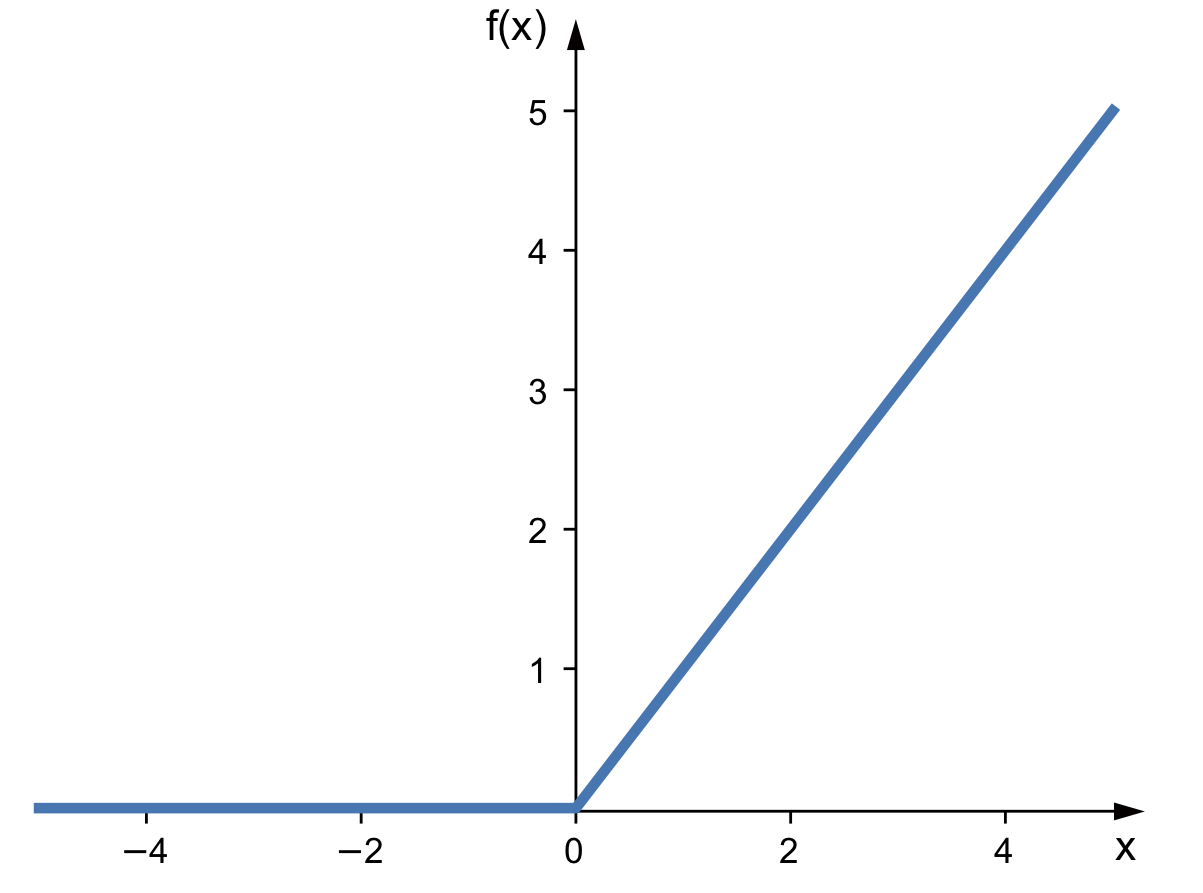
ReLU (Rectified Linear Unit)
Definición
\[ReLU(z) = max(0, z)\]
Propiedades
- Acota su salida entre 0 e \(\infty\).
- Su derivada es \(ReLU'(z) = \begin{cases} 1, & \text{if $z \ge$ 0} \\ 0 & \text{if $z < 0$} \end{cases}\)
- Es la función de activación más utilizada en la actualidad, principalmente en las capas ocultas de las Redes Neuronales.
- Se hizo extremadamente popular por su simplicidad y efectividad en
Redes Convolucionales(CNNs).
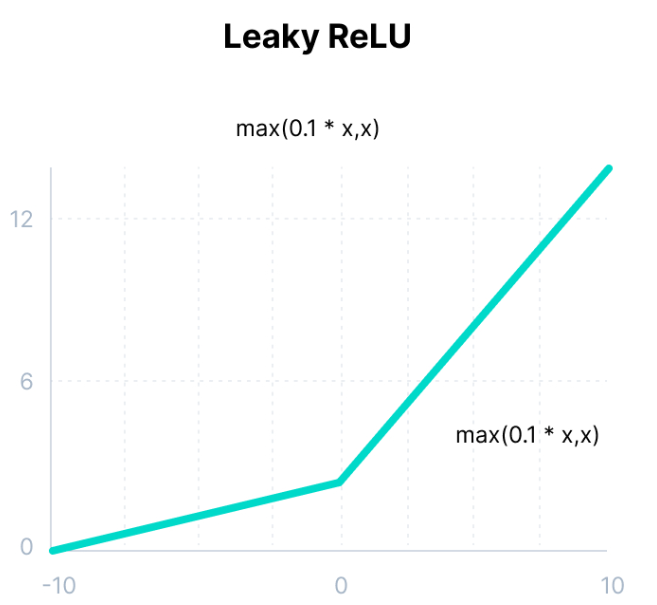
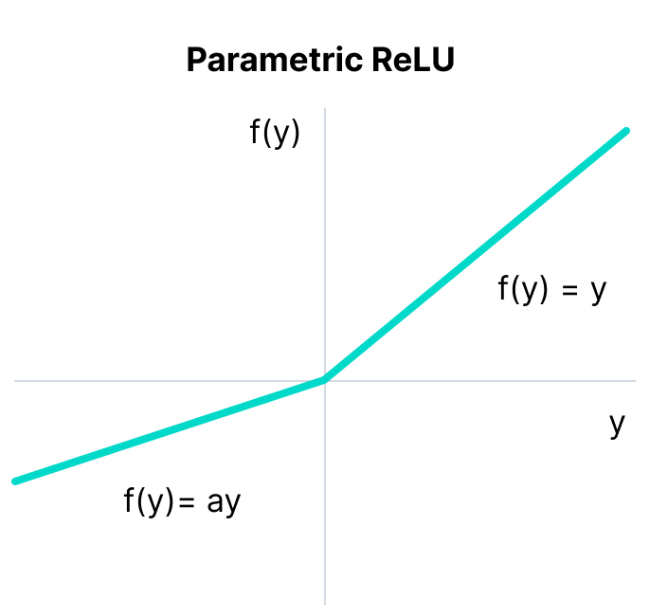
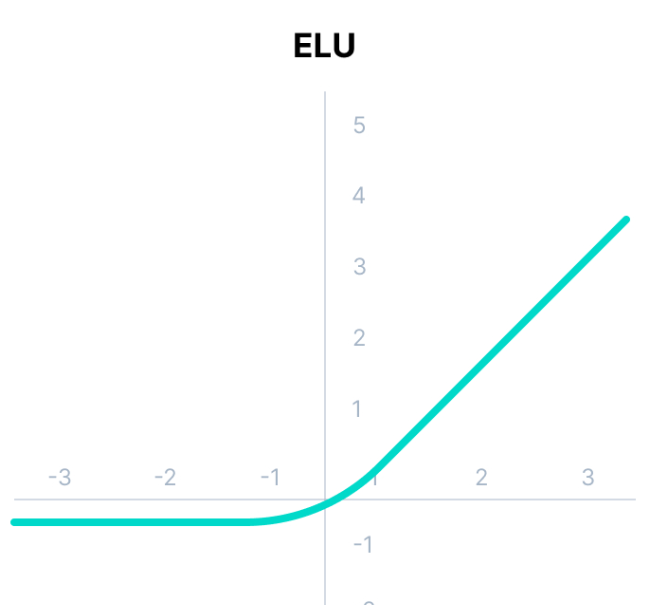
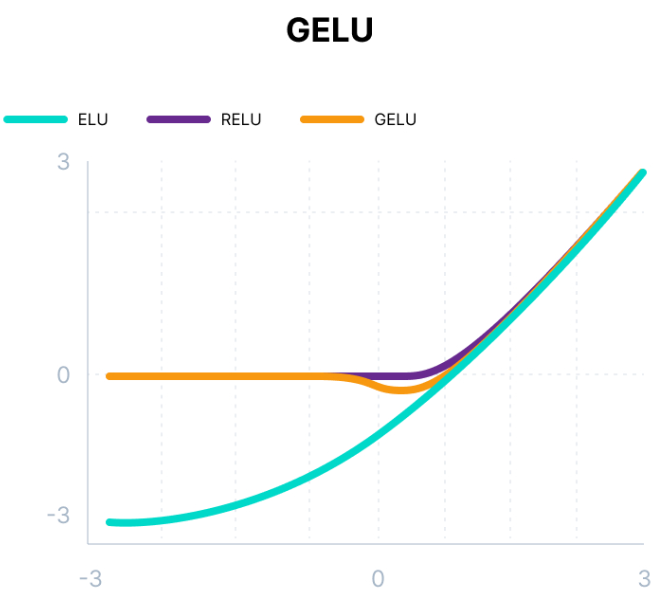
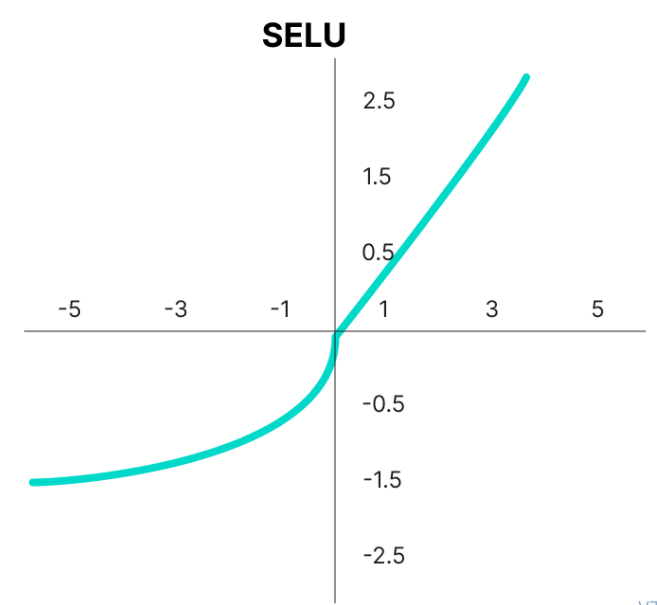
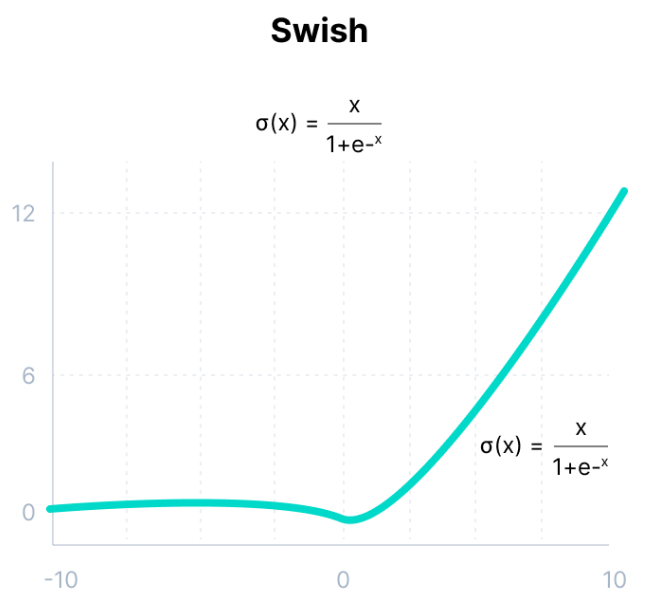
Funciones de Activación Modernas
Funciones de Activación
Funciones de Activación
Loss Functions: Clasificación
Son las encargadas de medir el error entre la predicción del modelo y el valor real. En general, se busca minimizar la Loss Function durante el entrenamiento del modelo.
Clasificación Binaria: Binary Cross Entropy
\[BCE(Z) = - \frac{1}{m}\left[y^T log(\sigma(Z)) + (1-y)^T log(1-\sigma(Z))\right]\]
Donde \(Z\) corresponden a los Logits del Modelo.
En Pytorch esta función se llama BCEWithLogitsLoss.
🤓 Logits
Se refiere a las activaciones finales del modelo antes de aplicar la función de activación.
👊 Clasificación Multilabel: BCEWithLogitsLoss
En Pytorch se suele utilizar BCEWithLogitsLoss ya que combina una sigmoide a cada activación de la salida.
Loss Functions: Clasificación
Clasificación Multiclase: CrossEntropy
\[CE(Z)= -\frac{1}{m}Tr(Y^T Log(\hat{Y}))\]
Donde \(Tr(.)\) es la traza de una matriz e \(Y \in \{0,1\}^{m \times k}\) es la codificación One-Hot de las etiquetas e \(\hat{Y} = Softmax(Z)\), donde \(Z\) son los Logits del modelo.
🤓 Traza (\(Tr(.)\))
Corresponde a la suma de los elementos de la diagonal principal de una matriz.
Derivada
\[\frac{\partial CE(X)}{\partial Z} = \frac{1}{m}\left(\hat{Y} - Y\right)\]
En Pytorch se suele utilizar CrossEntropyLoss ya que combina aplica una función Softmax a la capa de salida además de ser una clase numericamente más estable.
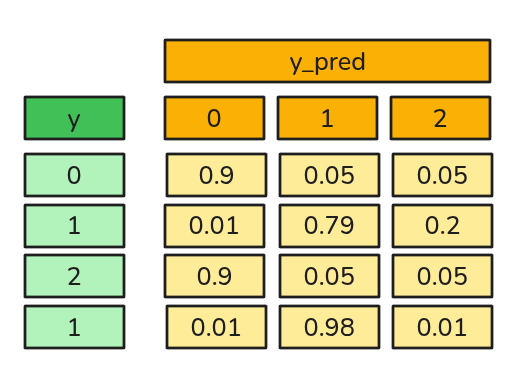
Ejemplo de Cálculo Cross Entropy Loss
\[Log(\hat{Y}) = \begin{bmatrix} -0.1054 & -2.9957 & -2.9957 \\ -4.6052 & -0.2357 & -1.6094 \\ -0.1054 & -2.9957 & -2.9957 \\ -4.6052 & -0.0202 & -4.6052 \end{bmatrix} \]
\[Y^T \cdot Log(\hat{Y}) = \begin{bmatrix} -0.1054 & ... & ... \\ ... & -0.2357 - 0.0202 & ... \\ ... & ... & -2.9957 \end{bmatrix} \]
Atención
Cada elemento de la diagonal acumula la contribución a la pérdida correspondiente a esa clase por parte de cada registro. Por ejemplo: la columna 1 contiene únicamente la pérdida del primer registro; la columna 2 acumula la pérdida del segundo y cuarto registro; y la columna 3 contiene solo la pérdida del tercer registro.
SPOILER: El logaritmo de los logits corresponde a la pérdida de cada registro.
La pérdida total la da la Traza de la matriz resultante. Luego la pérdida es: \(\frac{1}{4} [-0.1054 + (-0.2357 - 0.0202) + (-2.9957)] = 0.8392\).
Loss Functions: Regresión
Regresión: Mean Squared Error (MSELoss)
\[MSE(Z) = \frac{1}{m}||Z - \bar{y}||^2\]
Donde \(||.||\) corresponde a la norma Euclideana e \(\bar{y} \in \mathbb{R}^{m \times 1}\).
Derivada
\[\frac{\partial MSE(Z)}{\partial Z} = \frac{2}{m}(Z - \bar{y})\]
Loss Functions: Regresión
Regresión: Mean Absolute Error (L1Loss)
\[L1Loss(Z) = \frac{1}{m}|Z - \bar{y}|\]
Donde \(||.||\) corresponde a la norma Euclideana y \(\bar{y} \in \mathbb{R}^{m \times 1}\).
Derivada
\[\frac{\partial L1Loss(Z)}{\partial Z} = \frac{1}{m}sign(Z-\bar{y})\]
\[\operatorname{sign}(z) = \begin{cases} +1 & \text{si z > 0},\\[2mm] 0 & \text{si z = 0},\\[1mm] -1 & \text{si z < 0} \end{cases}\]
Optimizers: Gradient Descent
Gradient Descent corresponde al algoritmo de Optimización más popular, pero no necesariamente el más eficiente. Distintas variantes han ido apareciendo para ir mejorando eventuales deficiencias de la proposición inicial.
Epochs
Corresponden a la cantidad de iteraciones que se realizan a la Update Rule para que el modelo se optimize.
Standard Gradient Descent
\[\theta := \theta - \frac{\alpha}{m}\nabla_\theta L\]
Importante
- En Deep Learning, los conjuntos de datos suelen ser tan grandes que calcular el gradiente sobre todos ellos es inviable por memoria y tiempo de cómputo.
- Adicionalmente no basta con calcular el gradiente una vez, sino que se debe hacer varias veces según el número de Epochs definido.
- Practicar Standard Gradient Descent en la práctica es muy poco común, ya que no es eficiente.
Minibatch Gradient Descent
Los minibatches permiten estimar el gradiente con un subconjunto de datos, manteniendo la dirección correcta para actualizar los parámetros de manera más eficiente. Se realiza en un subconjunto de \(B\) datos donde \(B << m\).
\[\theta := \theta - \frac{\alpha}{B}\nabla_\theta L\]
👀 Importante
- \(X \in \mathbb{R}^{B \times n}\) e \(y \in \mathbb{R}^{B \times 1}\) son versiones reducidas de los datos totales. Se deben hacer suficientes
minibatchespara utilizar todos los datos. El minibatch se implementa en Pytorch utilizando elDataLoader. Cada actualización de parámetros ahora se le denominastep. - Cuando todos los
minibatcheshan sido utilizados, se dice que se ha completado unaepoch. - Es común utilizar un
minibatchde tamaño 32, 64, 128, etc. - A veces se deshecha el último
minibatch(remanente) si no tiene el tamaño completo para evitar problemas de estabilidad de gradientes.
Pros
- Permite optimizar utilizando menos recursos computacionales.
- Al actualizar los parámetros de manera más frecuente, se puede converger más rápido.
Contras
- Si \(B\) es muy pequeño, el gradiente puede ser muy ruidoso y no converger.
- El entrenamiento toma más tiempo que el Standard Gradient Descent.
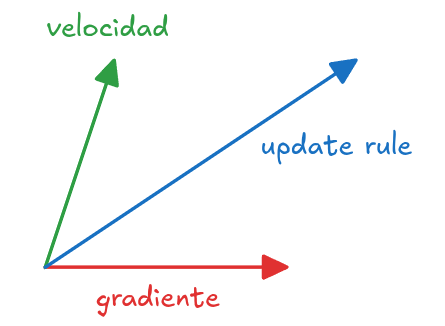
SGD with Momentum
Update Rule
\[\theta_{t+1} = \theta_t - \alpha v_{t + 1}\] \[v_{t+1} = \beta v_{t} + (1-\beta) \nabla_\theta L(\theta_{t+1})\]
donde \(0<\beta<1\), pero normalmente \(\beta=0.9\).
☝️ Intuición
- Este cálculo se denomina un Exponential Moving Average de los Gradientes. Y se puede interpretar como una especie de velocidad del gradiente. Su objetivo es ponderar con un cierto porcentaje el gradiente actual y el gradiente anterior.
- \(v_{0} = 0\)
\[\begin{align} v_{t+1}&=(1-\beta)\nabla_\theta L(\theta_{t}) + \beta v_t \\ v_{t+1}&=(1-\beta)\nabla_\theta L(\theta_{t}) + \beta \left[(1-\beta) \nabla_\theta L(\theta_{t-1}) + \beta v_{t-1}\right] \\ v_{t+1}&=(1-\beta)\nabla_\theta L(\theta_{t}) + \beta (1-\beta) \nabla_\theta L(\theta_{t-1}) + \beta^2 (1-\beta) \nabla_\theta L(\theta_{t-2})... \\ \end{align}\]
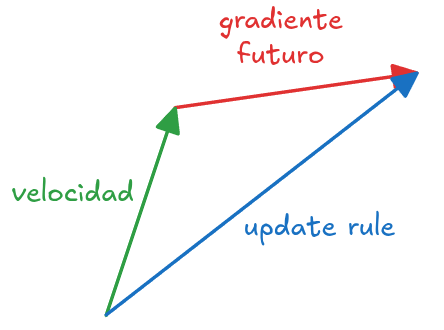
SGD with Nesterov Momentum
\[\theta_{t+1} = \theta_t - \alpha u_{t + 1}\] \[v_{t + 1} = \beta v_t + (1-\beta) \nabla_\theta f(\theta_{t+1} + \beta v_t)\]
donde \(0<\beta<1\), pero normalmente \(\beta=0.9\).
☝️ Intuición
El método de Nesterov “mira hacia adelante” en la dirección del momentum antes de calcular el gradiente, lo que le da una corrección más precisa y evita en parte el sobrepaso de mínimos. En este caso \(\theta_{t+1} + \beta v_t\) es el punto “futuro” para calcular el gradiente.
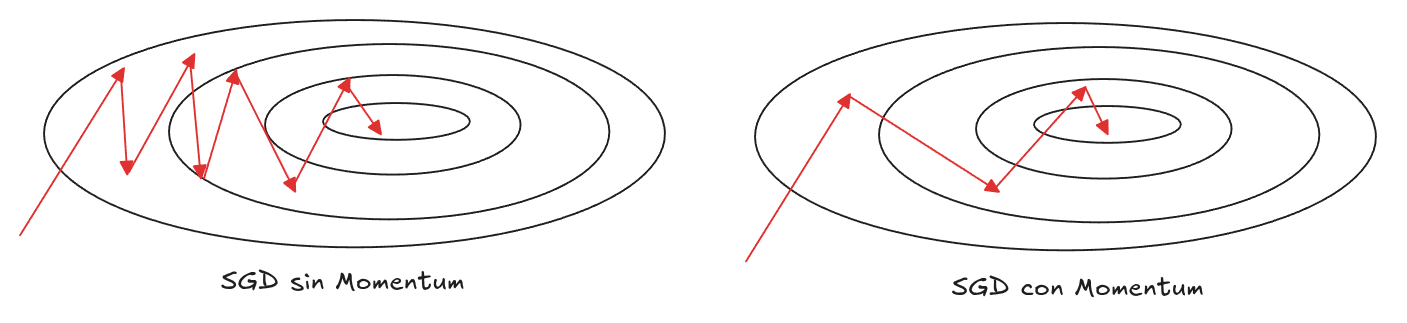
Efecto del Momentum en el Update Rule
☝️ Intuición
- El SGD tiende a ser más oscilante.
- El SGD con Momentum tiende a ser más suave y rápido debido a la inercia recibida por el término de momentum.
Métodos Adaptativos: Adagrad
☝️ Intuición
¿Qué tal, si el learning rate se va adaptando en el tiempo y deja de ser estática?
\[r_{t+1} = r_t + \nabla_\theta f(\theta_t)^2\] \[\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{r_{t+1}}}\nabla_\theta f(\theta_t)\]
Efecto
- Parámetros con gradientes grandes \(\rightarrow\) tasa de aprendizaje disminuye más rápido.
- Parámetros con gradientes pequeños \(\rightarrow\) tasa de aprendizaje se mantiene más alta.
Pros
- Util cuando hay parámetros que se actualizan con distinta frecuencia.
- Acelera la convergencia en direcciones poco exploradas.
Contras
- Como el denominador acumula gradientes al cuadrado, la tasa de aprendizaje puede llegar a volverse muy pequeña \(\rightarrow\) el entrenamiento se “frena” antes de llegar al óptimo.
Métodos Adaptativos: RMSProp
☝️ Intuición
- Normalizar por el Exponential Moving Average de los Gradientes al cuadrado para controlar el efecto de reducción del learning rate.
\[s_{t+1} = \beta r_t + (1-\beta) \nabla_\theta f(\theta_t)^2\] \[\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{s_{t+1}}}\nabla_\theta f(\theta_t)\]
Pros
- Normalización adaptativa: cada parámetro tiene su propia tasa de aprendizaje ajustada dinámicamente.
- A diferencia de Adagrad, el denominador no crece indefinidamente porque el promedio exponencial “olvida” gradientes antiguos. Esto permite seguir aprendiendo incluso después de muchos pasos.
Contras
- Depende mucho de la elección de su hiperparámetro \(\beta\)
Métodos Adaptativos: Adam
☝️ Intuición
Se mantiene el Exponential Moving average para: Los gradientes (como utilizando momentum), los gradientes al cuadrado (como RMSprop).
\[v_{t+1} = \beta_1 v_t + (1-\beta_1) \nabla_\theta f(\theta_t)\] \[s_{t+1} = \beta_2 s_t + (1-\beta_2) \nabla_\theta f(\theta_t)^2\] \[\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{s'_{t+1}}} v'_{t+1}\]
Correcciones Iniciales
\[v'_{t+1} = \frac{v_{t+1}}{1-\beta_1^{t+1}}\] \[s'_{t+1} = \frac{s_{t+1}}{1-\beta_2^{t+1}}\]
Pros
- Combina momentum + RMSprop + corrección \(\rightarrow\) rápido, estable.
- Es por lejos el optimizador más usado.
Contras
- Sensible a la elección de sus hiperparámetros \(\beta_1\) y \(\beta_2\). Pytorch utiliza 0.9 y 0.999 como valores de \(\beta_1\) y \(\beta_2\) respectivamente.
👊 Eso es todo amigos