TICS-579-Deep Learning

Clase 5: Training Tips & Tricks

Alfonso Tobar-Arancibia

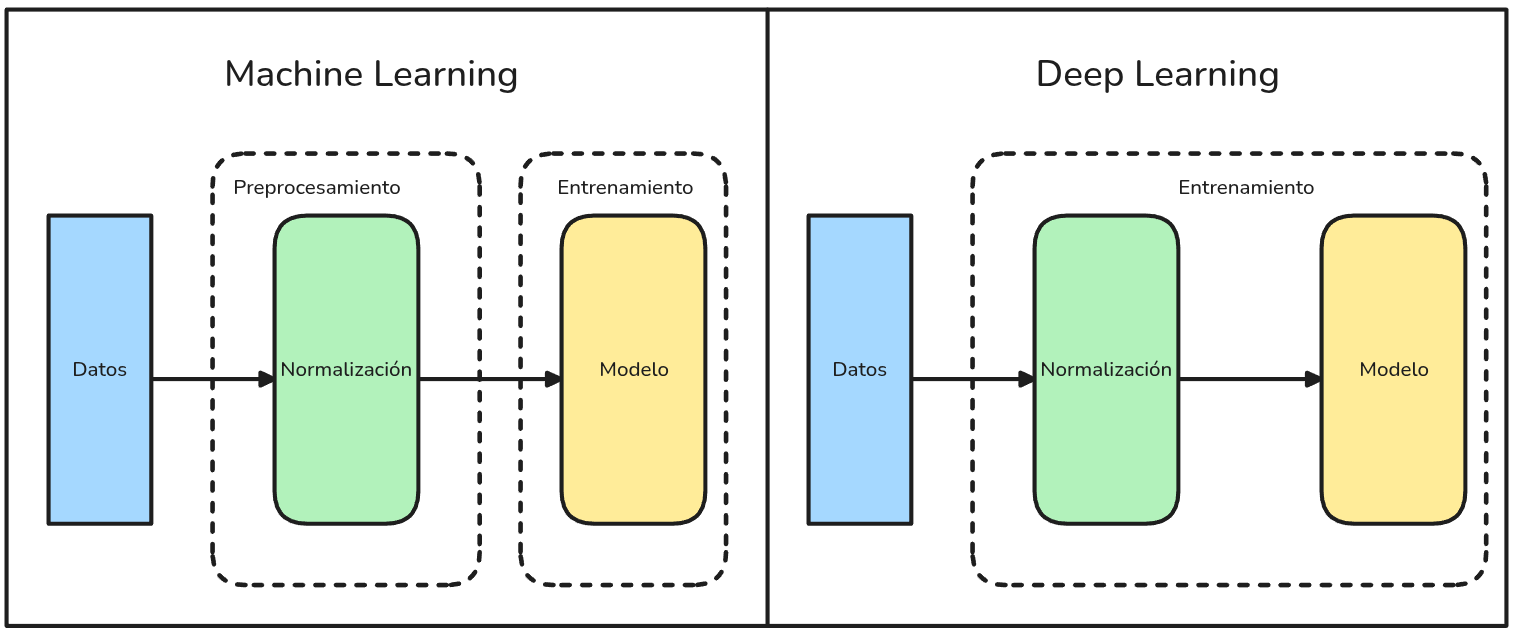
Machine Learning vs Deep Learning Workflow

Machine Learning

El proceso completo de entrenamiento del modelo se divide en dos etapas: preprocesamiento de datos y entrenamiento del modelo.

Deep Learning

El entrenamiento del modelo abarca tres etapas: preprocesamiento de datos, diseño de la arquitectura y entrenamiento propiamente tal como uno solo.

Preprocesamiento

Algunos de los problemas más comunes para los que se requieren preprocesamientos en Deep Learning son:

Encoding de Variables Categóricas

  • One Hot Encoding
  • Embeddings

Problemas de Escala:

  • Estandarización
  • Normalización
  • Normalization Layers

Problemas de Convergencia y combate contra el Overfitting:

  • Regularización L2 (Weight Decay)
  • Dropout
  • Weights Initialization

Problemas de Recursos Computacionales:

  • Checkpointing
  • Early Stopping
  • Gradient Accumulation

Problemas de Escala

En general el término Normalización está muy trillado y en la práctica se utiliza para referirse a muchos temas distintos. Algunas definiciones conocidas:

Normalización

\[x_{i\_norm} = \frac{x_i-x_{min}}{x_{max} - x_{min}}\] Esta operación se puede hacer mediante MinMaxScaler de Scikit-Learn.

Estandarización

\[ x_{i\_est} = \frac{x_i - E[x]}{\sqrt(Var[x])}\]

Esta operación se puede hacer mediante StandardScaler de Scikit-Learn.

👀 Ojo

La implementación de este tipo de técnicas normalmente requiere librerías externas a Pytorch (como Scikit-Learn o Feature Engine). Por lo que no es tan común en prácticas más avanzadas del área.

Alerta de Data Leakage

Utilizar estas estrategias externas pueden producir problemas de Data Leakage cuando se hace entrenamiento por Mini-Batches que es lo más común. Para evitar esto, lo más común es utilizar Normalization Layers dentro de la misma Arquitectura de la Red Neuronal.

Normalization Layers: Batch Normalization

Ioffe & Szegedy, 2015: Batch Normalization

Consiste en la primera implementación de una Normalización para cada Batch.

Pros

  • Resuelve el problema de Internal Covariate Shift.
  • Disminuye la importancia de los Parámetros iniciales e inicio del aprendizaje.
  • Genera un modelo más estable debido a que las activaciones están normalizadas.

Cons

  • Genera más parámetros entrenables y, por ende, más cálculos en la red.
  • Se complica el proceso de inferencia (test time).

Internal Covariate Shift

  • Al entrenar una red neuronal, cada capa depende de las salidas (activaciones) de la capa anterior.
  • Durante el entrenamiento, esas salidas cambian porque sus pesos se están actualizando, lo que implica que la distribución de entrada que ve cada capa está cambiando constantemente. Esto es lo que se conoce como internal covariate shift.

Esto significa que cada capa debe adaptarse continuamente a nuevas distribuciones de entrada, lo que ralentiza el entrenamiento y dificulta la convergencia.

Normalization Layers: Batch Norm, Punto de Partida

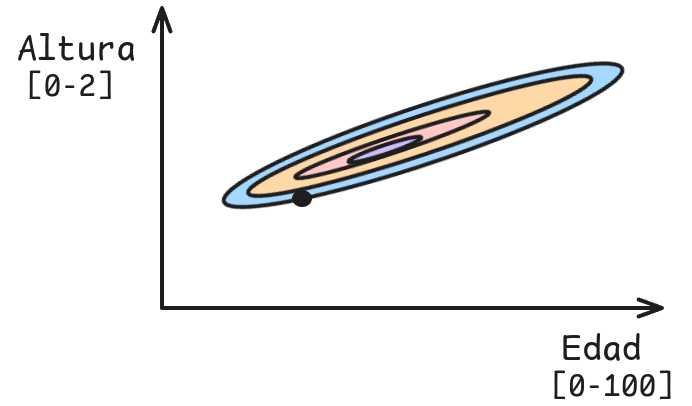
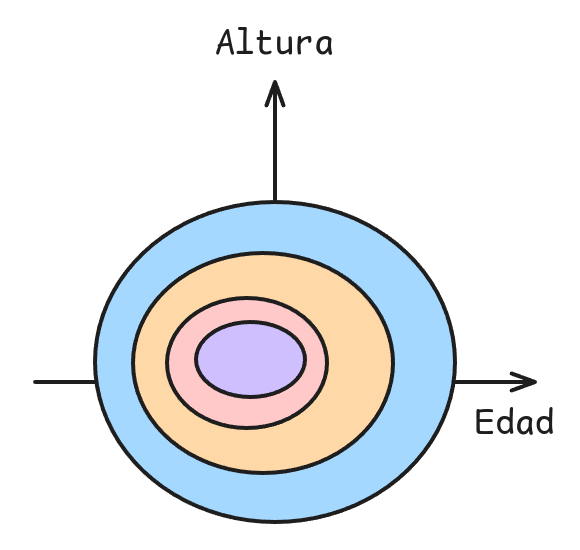
Ejemplo: Supongamos que dado la altura y la edad queremos predecir si será deportista de alto rendimiento.

Observaciones

  • Rango de Edad es mucho mayor que el de Altura.
  • Cambios en Altura deben ser mucho más pequeños que en Edad debido al rango.
  • Si el learning rate es alto puede diverger si nos movemos en la dirección de altura.
  • Si el learning rate es bajo, podría demorar mucho más en converger si nos movemos en la dirección de edad.

Observaciones

  • Sin importar el punto inicial, el mínimo se encuentra casi a la misma distancia.
  • Es posible utilizar un learning rate más grande sin miedo a diverger.

Batch Norm: Implementación (Forward Pass)

Supongamos el siguiente Batch de tamaño \(B=15\) con 3 features:

\[ X = \begin{bmatrix} 16 & 14 & 12 \\ 15 & 3 & 15 \\ 16 & 7 & 6 \\ 14 & 3 & 16 \\ 4 & 4 & 18 \\ 8 & 11 & 9 \\ 18 & 18 & 14 \\ 5 & 17 & 11 \\ 15 & 9 & 11 \\ 10 & 7 & 7 \end{bmatrix} \]

1. Calcular estadísticos de cada Batch: Promedio y Varianza.

\[\mu_B = \begin{bmatrix} 12.1 & 9.3 & 11.9 \end{bmatrix} \] \[ \sigma^2_B=\begin{bmatrix} 22.29 & 27.81 & 13.69 \end{bmatrix} \]

  • \(\sigma^2_B\) corresponde a la varianza sesgada (dividida por N).

2. Calcular normalización de cada Batch.

\[x_{norm} = \frac{X - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\]

3. Calcular Activación

\[h = \gamma \odot x_{norm} + \beta\]

Por defecto, Pytorch considera que \(\gamma = \begin{bmatrix} 1 & ... & 1 \end{bmatrix}\) y \(\beta = \begin{bmatrix} 0 & ... & 0 \end{bmatrix}\).

Luego \(\gamma\) y \(\beta\) son parámetros entrenables por el modelo. Tanto \(\gamma\) como \(\beta\) tienen la misma dimensión que el número de features (en este caso 3).

Batch Norm: Implementación (Forward Pass)

Cálculo Manual

eps = 1e-5
batch_mean = X.mean(dim=0, keepdim=True)
batch_var_train = X.var(dim=0, unbiased=False, keepdim=True)
x_norm = (X-batch_mean)/torch.sqrt(batch_var_train + eps)
w = torch.tensor([1,1,1])
b = torch.tensor([0,0,0])
w*x_norm + b
============================================================
Forward Pass Train obtenido Manualmente
============================================================
tensor([[ 0.8261,  0.8912,  0.0270],
        [ 0.6142, -1.1946,  0.8378],
        [ 0.8261, -0.4361, -1.5946],
        [ 0.4024, -1.1946,  1.1081],
        [-1.7157, -1.0050,  1.6486],
        [-0.8684,  0.3224, -0.7838],
        [ 1.2497,  1.6498,  0.5676],
        [-1.5038,  1.4601, -0.2432],
        [ 0.6142, -0.0569, -0.2432],
        [-0.4448, -0.4361, -1.3243]])

Cálculo en Pytorch

bn = nn.BatchNorm1d(3)
## Importantísimo ya que BatchNorm tiene distinto 
## funcionamiento en Modo Train y Eval
bn.train()
output_pytorch= bn(X)
output_pytorch
============================================================
Forward Pass en Modo Train utilizando Pytorch
============================================================
tensor([[ 0.8261,  0.8912,  0.0270],
        [ 0.6142, -1.1946,  0.8378],
        [ 0.8261, -0.4361, -1.5946],
        [ 0.4024, -1.1946,  1.1081],
        [-1.7157, -1.0050,  1.6486],
        [-0.8684,  0.3224, -0.7838],
        [ 1.2497,  1.6498,  0.5676],
        [-1.5038,  1.4601, -0.2432],
        [ 0.6142, -0.0569, -0.2432],
        [-0.4448, -0.4361, -1.3243]], grad_fn=<NativeBatchNormBackward0>)

Batch Norm: Implementación (Test Time)

Problema

La predicción de una instancia \(i\) específica, ahora depende de otros elementos dentro del Batch.

¿Cómo funciona entonces el modelo en Test Time?

1. Calcular running mean y running var.

\[ \begin{aligned} \mu_{running} &= (1 - \alpha) \mu_{running} + \alpha \cdot \mu_B \\ s^2_{running} &= (1 - \alpha) \cdot s^2_{running} + \alpha \cdot s^2_B \end{aligned} \]

Ojo: En este caso se usa la Varianza insesgada (dividida por N-1). \(\alpha\) es un hiperparámetro que mide la contribución del Batch actual a los estadísticos globales. Por defecto en Pytorch \(\alpha = 0.1\).

2. Calcular normalización de cada Batch.

\[x_{norm}^{test} = \frac{X - \mu_{running}}{\sqrt{s_{running}^2 + \epsilon}}\]

3. Calcular Activación

\[h = \gamma \cdot x_{norm}^{test} + \beta\]

En este caso, \(\gamma\) y \(\beta\) son parámetros aprendidos durante el entrenamiento.

Batch Norm: Implementación (Test Time)

Cálculo Manual

batch_var_eval = X.var(dim=0, unbiased=True, keepdim=True)

alpha = 0.1
rm = (1-alpha)*torch.tensor([0,0,0]) + alpha*batch_mean
rv = (1-alpha)*torch.tensor([1,1,1]) + alpha*batch_var_eval

x_normalized_eval = (X - rm)/torch.sqrt(rv + eps)
bn.weight.data*x_normalized_eval+bn.bias.data
============================================================
Test Time: 
============================================================
Media: 
tensor([[1.2100, 0.9300, 1.1900]])
Varianza: 
tensor([[3.3767, 3.9900, 2.4211]])
Forward Pass en Modo Evaluación obtenido de manera manual...
============================================================
tensor([[ 8.0487,  6.5432,  6.9473],
        [ 7.5045,  1.0363,  8.8753],
        [ 8.0487,  3.0388,  3.0913],
        [ 6.9603,  1.0363,  9.5180],
        [ 1.5183,  1.5369, 10.8034],
        [ 3.6951,  5.0413,  5.0193],
        [ 9.1370,  8.5457,  8.2327],
        [ 2.0625,  8.0451,  6.3046],
        [ 7.5045,  4.0400,  6.3046],
        [ 4.7835,  3.0388,  3.7339]])

Cálculo en Pytorch

bn.eval()
bn(X)
============================================================
Forward Pass en Modo Evaluación usando Pytorch...
============================================================
tensor([[ 8.0487,  6.5432,  6.9473],
        [ 7.5045,  1.0363,  8.8753],
        [ 8.0487,  3.0388,  3.0913],
        [ 6.9603,  1.0363,  9.5180],
        [ 1.5183,  1.5369, 10.8034],
        [ 3.6951,  5.0413,  5.0193],
        [ 9.1370,  8.5457,  8.2327],
        [ 2.0625,  8.0451,  6.3046],
        [ 7.5045,  4.0400,  6.3046],
        [ 4.7835,  3.0388,  3.7339]], grad_fn=<NativeBatchNormBackward0>)

Batch Norm: Consejos

  • Andrew Ng propone utilizar BatchNorm justo antes de la función de Activacion.
  • El paper original también propone su uso justo antes de la activación.
  • Francoise Chollet, creador de Keras dice que los autores del paper en realidad lo utilizaron después de la función de activación.
  • Adicionalmente existen benchmarks que muestran mejoras usando BatchNorm después de las funciones de activación.

Entonces, la posición del BatchNorm termina siendo parte de la Arquitectura, y se debe comprobar donde tiene un mejor efecto.

Batchnorm tiene efectos distintos al momento de entrenar o de evaluar/predecir en un modelo. Por lo tanto, de usar Batchnorm es imperativo utilizar los modos model.train() y model.eval().

Normalización: Layer Norm

Ley, Ryan, Hinton, 2016: Layer Normalization

Batch Norm tiene algunos problemas:

  • Muy difícil de calcular en datos secuenciales (lo veremos más adelante).
  • Inestable cuando el Batch Size es muy pequeño.
  • Difícil de Paralelizar.

Beneficios de Layer Norm

  • Puede trabajar con secuencias (Esencial para Transformers).
  • No tiene problemas para trabajar con cualquier tipo de Batch Size.
  • Se puede paralelizar, lo cuál es útil en redes como las RNN.
  • En este caso se realiza la normalización por instancia y no por Batch.

Normalización: Layer Norm

1. Calcular estadísticos de cada Instancia: Promedio y Varianza.

\[\mu = \begin{bmatrix} 14.0000 & 11.0000 & 9.6667 & 11.0000 & 8.6667 & 9.3333 & 16.6667 & 11.0000 & 11.6667 & 8.0000 \end{bmatrix}^T \]

\[ \sigma^2 = \begin{bmatrix} 2.6667 & 32.0000 & 20.2222 & 32.6667 & 43.5556 & 1.5556 & 3.5556 & 24.0000 & 6.2222 & 2.0000 \end{bmatrix}^T \]

  • \(\sigma^2_B\) corresponde a la varianza sesgada (dividida por N).

2. Calcular normalización de cada Instancia.

\[x_{norm} = \frac{X - \mu}{\sqrt{\sigma^2 + \epsilon}}\]

3. Calcular Activación

\[h = \gamma \odot x_{norm} + \beta\]

Por defecto, Pytorch considera que \(\gamma = \begin{bmatrix} 1 & ... & 1 \end{bmatrix}\) y \(\beta = \begin{bmatrix} 0 & ... & 0 \end{bmatrix}\).

Luego \(\gamma\) y \(\beta\) son parámetros entrenables por el modelo. Tanto \(\gamma\) como \(\beta\) tienen la misma dimensión que el número de features (en este caso 3).

Layer Norm: Implementación (Forward Pass)

Cálculo Manual

eps = 1e-5
sample_mean = X.mean(dim=1, keepdim=True)
sample_var = X.var(dim=1, unbiased=False, keepdim=True)
x_normalized = (X - sample_mean) / torch.sqrt(sample_var + eps)
print("="*60)
print("="*60)
ln.weight.data*x_normalized + ln.bias.data
============================================================
Forward Pass Obtenido de manera Manual
============================================================
tensor([[ 1.2247,  0.0000, -1.2247],
        [ 0.7071, -1.4142,  0.7071],
        [ 1.4084, -0.5930, -0.8154],
        [ 0.5249, -1.3997,  0.8748],
        [-0.7071, -0.7071,  1.4142],
        [-1.0690,  1.3363, -0.2673],
        [ 0.7071,  0.7071, -1.4142],
        [-1.2247,  1.2247,  0.0000],
        [ 1.3363, -1.0690, -0.2673],
        [ 1.4142, -0.7071, -0.7071]])

Cálculo en Pytorch

ln = nn.LayerNorm(3)
output_pytorch = ln(X)
output_pytorch
============================================================
Forward Pass obtenido utilizando Pytorch
============================================================
tensor([[ 1.2247,  0.0000, -1.2247],
        [ 0.7071, -1.4142,  0.7071],
        [ 1.4084, -0.5930, -0.8154],
        [ 0.5249, -1.3997,  0.8748],
        [-0.7071, -0.7071,  1.4142],
        [-1.0690,  1.3363, -0.2673],
        [ 0.7071,  0.7071, -1.4142],
        [-1.2247,  1.2247,  0.0000],
        [ 1.3363, -1.0690, -0.2673],
        [ 1.4142, -0.7071, -0.7071]], grad_fn=<NativeLayerNormBackward0>)

Normalization: RMSNorm

1. Calcular Root Mean Square de cada Instancia.

\[RMS(X)= \sqrt{\frac{1}{d} \sum_{i=1}^{d} X^2 + \epsilon}\]

2. Calcular normalización de cada Instancia.

\[x_{norm} = \frac{X}{RMS(X)}\]

3. Calcular Activación

\[h = \gamma \odot x_{norm}\]

Por defecto, Pytorch considera que \(\gamma = \begin{bmatrix} 1 & ... & 1 \end{bmatrix}\).

Luego \(\gamma\) son parámetros entrenables por el modelo. \(\gamma\) tienen la misma dimensión que el número de features (en este caso 3).

RMSNorm: Implementación

Cálculo Manual

rms = torch.sqrt((X**2).mean(dim=1, keepdims = True))
rms_layer.weight.data*X/rms
============================================================
Forward Pass Obtenido de manera Manual
============================================================
tensor([[1.1352, 0.9933, 0.8514],
        [1.2127, 0.2425, 1.2127],
        [1.5007, 0.6566, 0.5628],
        [1.1294, 0.2420, 1.2907],
        [0.3672, 0.3672, 1.6524],
        [0.8496, 1.1682, 0.9558],
        [1.0732, 1.0732, 0.8347],
        [0.4152, 1.4118, 0.9135],
        [1.2573, 0.7544, 0.9220],
        [1.2309, 0.8616, 0.8616]])

Cálculo en Pytorch

rms_layer = nn.RMSNorm(3)
rms_layer(X)
============================================================
Forward Pass Obtenido utilizando Pytorch
============================================================
tensor([[1.1352, 0.9933, 0.8514],
        [1.2127, 0.2425, 1.2127],
        [1.5007, 0.6566, 0.5628],
        [1.1294, 0.2420, 1.2907],
        [0.3672, 0.3672, 1.6524],
        [0.8496, 1.1682, 0.9558],
        [1.0732, 1.0732, 0.8347],
        [0.4152, 1.4118, 0.9135],
        [1.2573, 0.7544, 0.9220],
        [1.2309, 0.8616, 0.8616]], grad_fn=<MulBackward0>)

Regularización L2 aka Weight Decay

Paper 1991: Weight Decay

En general, el principal problema de las redes neuronales es el overfitting, ya que estas redes suelen ser consideradas modelos sobredimensionados (overparameterized models). ¿Qué implica esto exactamente?

Weight Decay

Corresponde a una penalización que se da a los modelos para limitar su complejidad y asegurar que pueda generalizar correctamente en datos no vistos.

\[ \underset{W_{i:L}}{minimize} \frac{1}{m} L + \frac{\lambda}{2} \sum_{i=1}^L ||W_i||_f^2\]

Regularización L2 aka Weight Decay

Eso implica una transformación a nuestro Update Rule:

\[W_i := W_i - \alpha \frac{1}{m} \nabla L - \alpha \lambda W_i = (1-\alpha\lambda)W_i - \alpha \nabla L\]

Se puede ver que los pesos (weights) se contraen (decaen) antes de actualizarse en la dirección del gradiente. Lo que genera parámetros más pequeños y, por ende, un modelo más simple.

Por alguna razón Pytorch decidió implementarlo como una propiedad de los Optimizers cuando en realidad debió ser de la Loss Function.

torch.optim.Adam(model.parameters(), lr=3e-4, weight_decay=0.3)

En este caso 0.3 corresponde al valor de \(\lambda\).

Dropout

Paper 2014: Dropout

Definiremos el Dropout como:

\[D(h)= \begin{cases} \frac{h}{1-p} & \text{con prob 1-p} \\ 0, & \text{con prob p} \end{cases}\]

donde \(D\) implica la aplicación de Dropout a la activación \(h\). \(p\) se conoce como el Dropout Rate.

El factor \(\frac{1}{1-p}\) se aplica para mantener la varianza estable luego de haber eliminado activaciones con probabilidad \(p\).

Dropout se aplica normalmente al momento de entrenar el modelo. Por lo tanto, de usar Dropout es imperativo cambiar al modo model.eval() al momento de predecir.

Weights Initialization

Paper 2010: Xavier Initialization

Paper 2015: Kaiming Initialization

Hasta ahora, hemos inicializado los pesos de las redes neuronales de forma aleatoria. Sin embargo, diversos estudios han explorado estrategias de inicialización de los parámetros para lograr una convergencia más eficiente. Entre las técnicas más comunes se encuentran:

Activaciones Triviales

  • Constante
  • Sólo unos
  • Sólo Zeros
  • Con Distribución Uniforme
  • Con Distribución Normal

Weights Initialization

Xavier o Glorot Uniforme

Se inicia con valores provenientes de una distribución uniforme: \(\mathcal{U}(-a,a)\)

\[ a = gain \cdot \sqrt{\frac{6}{fan_{in} + fan_{out}}}\]

Xavier o Glorot Normal

Se inicia con valores provenientes de una distribución Normal: \(\mathcal{N}(0,std^2)\)

\[ std = gain \cdot \sqrt{\frac{2}{fan_{in} + fan_{out}}}\]

  • \(fan_{in}\) corresponde al número de conexiones que entran a una neurona. Mientras que \(fan_{out}\) corresponde al número de neuronas que salen de dicha neurona.
  • \(fan\_mode\) corresponde a la elección de \(fan_{in}\) o \(fan_{out}\).

Kaiming (aka He) Uniforme

Se inicia con valores provenientes de una distribución Uniforme: \(\mathcal{U}(-bound,bound)\)

\[ bound = gain \cdot \sqrt{\frac{3}{fan\_mode}}\]

Kaiming (aka He) Normal

Se inicia con valores provenientes de una distribución Normal: \(\mathcal{N}(0,std^2)\)

\[std =\sqrt{\frac{gain}{fan\_mode}}\]

Checkpointing

Entrenar una red neuronal puede requerir una gran cantidad de tiempo y recursos computacionales. Por ello, es una buena práctica guardar los pesos del modelo en distintos momentos del entrenamiento, con el fin de no perder el progreso alcanzado ante posibles imprevistos (como un corte de energía o un fallo del sistema).

Esto ofrece varias ventajas, entre ellas:

  • Poder disponer de resultados intermedios incluso si el entrenamiento aún no finaliza.
  • Almacenar los pesos correspondientes al mejor modelo obtenido durante el proceso de entrenamiento.

Checkpoints

Pytorch permite el uso de Checkpointing de manera sencilla mediante la función torch.save() y torch.load().

Algunas estrategias comunes de Checkpointing son:

  • Guardar el modelo cada cierto número de epochs.
  • Guardar el modelo cuando se alcanza un nuevo mejor desempeño en el conjunto de validación.
  • Guardar tanto el modelo como el optimizador para poder reanudar el entrenamiento desde el último checkpoint. En especial cuando existen restricciones de tiempo en el uso de recursos computacionales.
  • Guardar el modelo antes de alcanzar el Overfitting.
  • Guardar el modelo final al concluir el entrenamiento.
  • Guardar modelos intermedios para analizar si se va por buen camino.

Early Stopping

El Early Stopping consiste en monitorear el rendimiento sobre un conjunto de validación durante el entrenamiento y detener el proceso cuando el rendimiento comienza a empeorar. De esta manera, se evita invertir tiempo y recursos computacionales en seguir entrenando un modelo que ya no mejora su capacidad de generalización.

Grokking

Un nuevo concepto que anda dando vuelta en el último tiempo es el grokking. El cuál es una mejora del performance del modelo pasado el punto de overfitting. Por lo que el Early Stopping podría impedir que se alcance este punto.

En general este proceso detiene el entrenamiento luego de patience epochs sin mejorar el validation loss u otro criterio. Una lógica simple para implementarlo es agregar lo siguiente al training loop:

# ---- Early Stopping ----
    if val_loss > best_val_loss:
        best_val_loss = val_loss
        best_model_state = model.state_dict()
        counter = 0  # resetea paciencia
    else:
        counter += 1
        if counter >= patience:
            print(f"Early stopping en epoch {epoch+1}")
            break

Gradient Accumulation

Otra estrategia para enfrentar limitaciones de memoria es el Gradient Accumulation. Esta técnica permite simular batch sizes más grandes al acumular los gradientes durante varios pasos. De esta forma, se obtienen resultados equivalentes a los de un entrenamiento con batches grandes, pero utilizando menos recursos computacionales (a costa de requerir más iteraciones o epochs).

## Training with Accumulation
accumulation_steps=4
model.zero_grad()                                   # Resetea Gradientes Iniciales
for e in range(epochs):
  logits = model(X)                     
  loss = criterion(logits, y.unsqueeze(-1))
  print(f"Epoch: {e+1}. Loss: {loss.item()}")
  loss = loss / accumulation_steps                # Normaliza Loss
  loss.backward()                                 # Backward pass 
  # (Recordar que Pytorch Acumula Gradientes hasta que se use .zero_grad())
  if (e+1) % accumulation_steps == 0:             
      optimizer.step()                            # Se actualizan pesos sólo cada ciertos steps
      model.zero_grad()                           # Y ahora se resetea

That’s all Folks

Tics-579 Deep Learning por Alfonso Tobar-Arancibia está licenciado bajo CC BY-NC-SA 4.0