TICS-579-Deep Learning

Clase 6: Redes Convolucionales

Alfonso Tobar-Arancibia

alfonso.tobar.a@edu.uai.cl

Limitaciones de las FFN

Sin duda las Redes Feed Forward son una herramienta poderosa para resolver problemas de clasificación y regresión. Sin embargo, presentan ciertas limitaciones cuando se aplican a datos con estructuras espaciales o temporales, como imágenes o secuencias de texto.

⚠️ Pérdida de estructura espacial o secuencial

Cada registro es considerado de manera independiente, sin tener en cuenta la relación espacial o secuencial entre los datos.

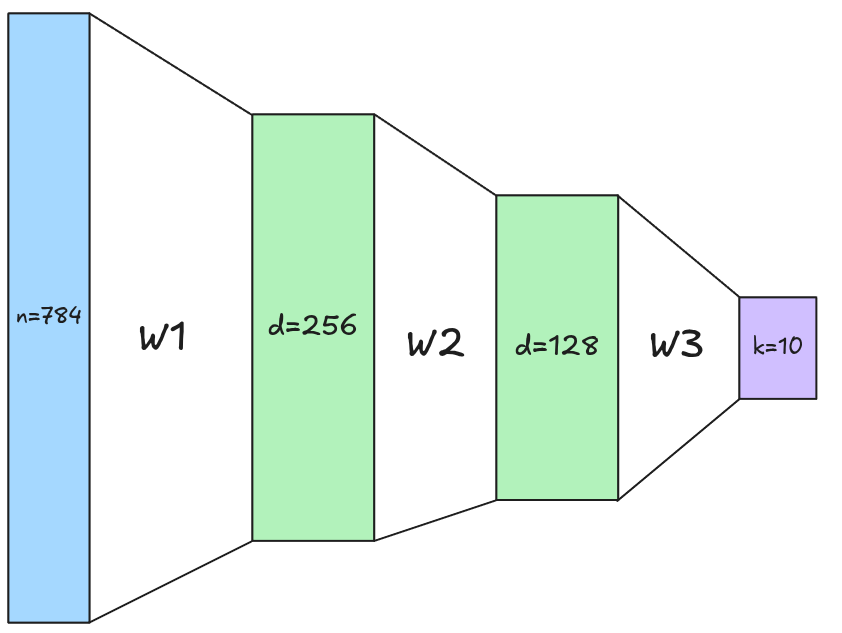
☢️ Gran cantidad de parámetros

Número de Parametros

(Imagen: 28x28=784 píxeles):

\(W_1 = 784 \cdot 256 + 256 = 200960\)
\(W_2 = 256 \cdot 128 + 128 = 32896\)
\(W_3 = 128 \cdot 10 + 10 = 1290\)
Total = 235,146.

¿Y si tengo una imágen de \(512 \times 512\)? 67,143,306 de parámetros.

Limitaciones de las FFN

🚧 Ineficiencia en el aprendizaje de patrones locales

Translation Invariance: Se refiere a la capacidad de poder detectar un patrón/objeto en diferentes posiciones de la imágen.

Problema: Un perrito centrado, desplazado a la izquierda o a la derecha debería seguir siendo reconocido como un perrito. Para una FFN, las features que describen los perritos desplazados son completamente distintos.

Limitaciones de las FFN

⛔ Escalabilidad Limitada

Su alto número de parámetros sumado a la incapacidad de capturar patrones espaciales o temporales hace que las FFN no escalen bien a datos complejos como imágenes de alta resolución o secuencias largas haciendo que su rendimiento disminuya considerablemente y no sean aplicables por sí solas a casos reales.

Imagenes actuales cada vez más grandes

Textos actuales cada vez más largos

Imágenes

Imagen: Definiremos una imágen como un Tensor de Orden 3. Normalmente cada dimensión representa H, W y C (Altura, Ancho y Canales).

Convención en Pytorch

Pytorch utiliza la convención (C, H, W) para representar imágenes, donde C es el número de canales, H es la altura y W es el ancho de la imagen. Es decir, un Tensor de Dimensiones (3, 512, 512)

La convención más común es utilizar imágenes de 24-bits, es decir 3 canales de \(2^8\) valores (8-bits por canal). Es por eso que el valor de los píxeles va de 0 a 255 y representan la intensidad del color del canal que representan.

Imágenes

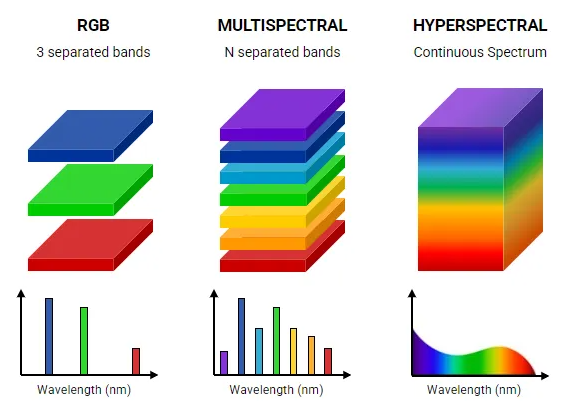
Librerías como PIL u OpenCV permiten importar imágenes en Python. Ambas usan la convención de \((H,W,C)\), la diferencia está en el orden de los canales. PIL utiliza la convención RGB, mientras que OpenCV utiliza BGR por lo que se necesitan algunas transformaciones adicionales.

Ejemplo para importar imágenes con PIL y Pytorch

from PIL import Image
import numpy as np
import torch
path = "path/to/imagen.png"
img = Image.open(path)

# Convierte a Tensor y cambia a (C,H,W)
torch_image= torch.from_numpy(np.array(img)).permute(2,0,1)  
torch_image.shape

(3,1200,1200)

import matplotlib.pyplot as plt

## Imágen en canal Rojo
plt.imshow(torch_image[0].numpy(), cmap="Reds")
plt.axis("off")
plt.show()
## Imágen en canal Verde
plt.imshow(torch_image[1].numpy(),cmap="Greens")
plt.axis("off")
plt.show()
## Imágen en canal Azul
plt.imshow(torch_image[2].numpy(), cmap="Blues")
plt.axis("off")
plt.show()

Batch de Imágenes

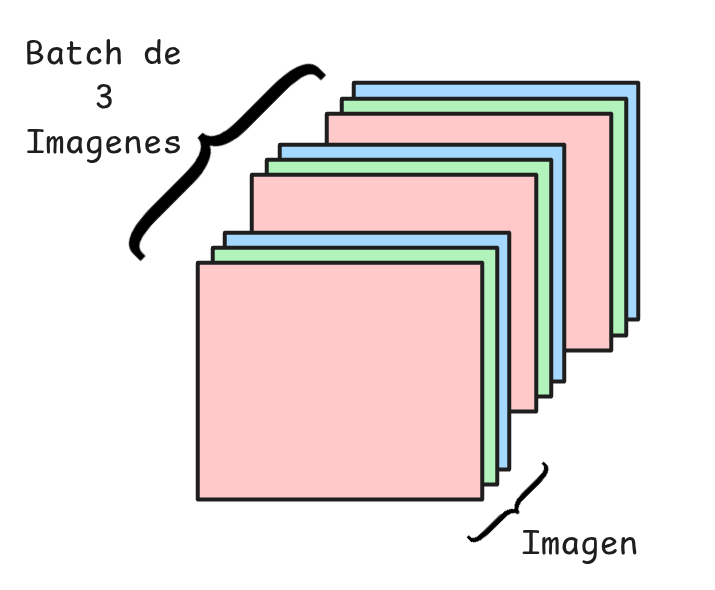
Conjunto/Set/Batch de Imágenes

Se define como un Tensor de Orden 4. En Pytorch esto se representa como N, C, H, W (Número de Imágenes, Canales, Altura y Ancho).

Luego un Tensor de Dimensiones (32,3,224,512) implica que tenemos 32 imágenes RGB de dimensiones \(224\times512\).

## Simulación de 2 imágenes RGB de 5x5 píxeles
torch.randint(0,256, (2,3,5,5))

tensor([[[[248, 240, 146,  73, 228],
          [ 79, 125, 191, 203, 133],
          [202,  12, 237, 109,  62],
          [133, 227, 148,  78, 229],
          [121, 247, 202,  51,   3]],

         [[253,  28,  20, 144, 255],
          [115, 132, 114,  45, 164],
          [ 57, 238, 117, 250,  41],
          [ 58,  73,  29, 253, 240],
          [246,  84,  93,   2, 145]],

         [[ 83,   4, 144, 126, 202],
          [ 98, 235,  55,  83, 104],
          [ 21, 185,  27, 102, 117],
          [255, 133,  23,  83, 150],
          [ 49, 152,  81, 233,  98]]],
-----------------------------------------------
        [[[216,  92, 251, 214, 178],
          [252,  48,  88,  82,  79],
          [168, 208, 223,   9, 169],
          [145, 148, 254, 128, 156],
          [238, 175, 233, 136, 118]],

         [[112,  68, 143,  93, 150],
          [ 32, 103,  97,  93, 223],
          [205,  56,  90,  24, 108],
          [ 13, 135,  98,  20,  93],
          [ 20,  91,  37,  81,  10]],

         [[109, 145,  90, 243,  63],
          [103, 134, 130,  11,  72],
          [132, 163, 153,  26, 255],
          [ 45, 228,  26, 169, 212],
          [ 34, 211, 229,  82, 201]]]])

Redes Convolucionales: Definición e Inspiración

Redes Convolucionales (CNN): Son un tipo de red neuronal cuyos parámetros entrenables son filtros (también llamados Kernels) que aprenden a detectar patrones en los datos de entrada.

El resultado de una Convolucional es un feature map, el cual representa la presencia y localización de ciertos patrones visuales.

Existe el mito de que las Redes Convolucionales se inspiraron en el funcionamiento del Cortex Visual humano. No sé si es tan así.

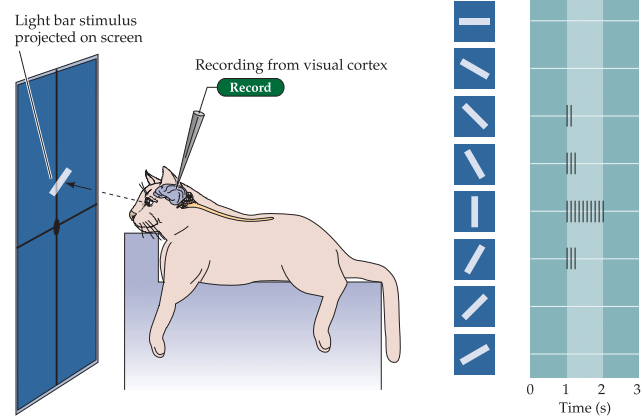
El mito dice que las CNNs fueron diseñadas para imitar el cortex visual humano. Esto viene de los trabajos de Hubel y Wiesel (década de 1960), que estudiaron cómo las neuronas en la corteza visual de gatos respondían a estímulos:

Descubrieron neuronas simples que respondían a líneas en cierta orientación y posición.
Descubrieron neuronas complejas que respondían a patrones similares, pero en distintas posiciones (invarianza local).

Redes Convolucionales: Definición e Inspiración

¿Por qué necesitamos las Redes Convolucionales? Evitar la sobreparametrización. ¿Por qué esto es un problema?

🔔 Importancia

No es exagerado afirmar que las CNNs han sido la arquitectura más influyente en Deep Learning, ya que han impulsado avances importantes en tareas de visión por computador, como clasificación de imágenes, detección de objetos y segmentación semántica. Además, contribuyeron a que el Deep Learning ganara popularidad en la industria tecnológica y superara la época conocida como el AI Winter.

🗓️ Algunos hitos importantes:

1990: Yann LeCun et al. propone uno de los primeros intentos de CNN, el cual va agregando features más simples en features más complejas progresivamente.
1998: Yann LeCun, propone LeNet-5 con 2 redes convolucionales y 3 FFN.
2012: Krizhevsky, Sutskever y Hinton proponen AlexNet (5 capas convolucionales y 3 FFN), el cual obtiene SOTA performance en ImageNet.

Convolutional Neural Network (CNNs)

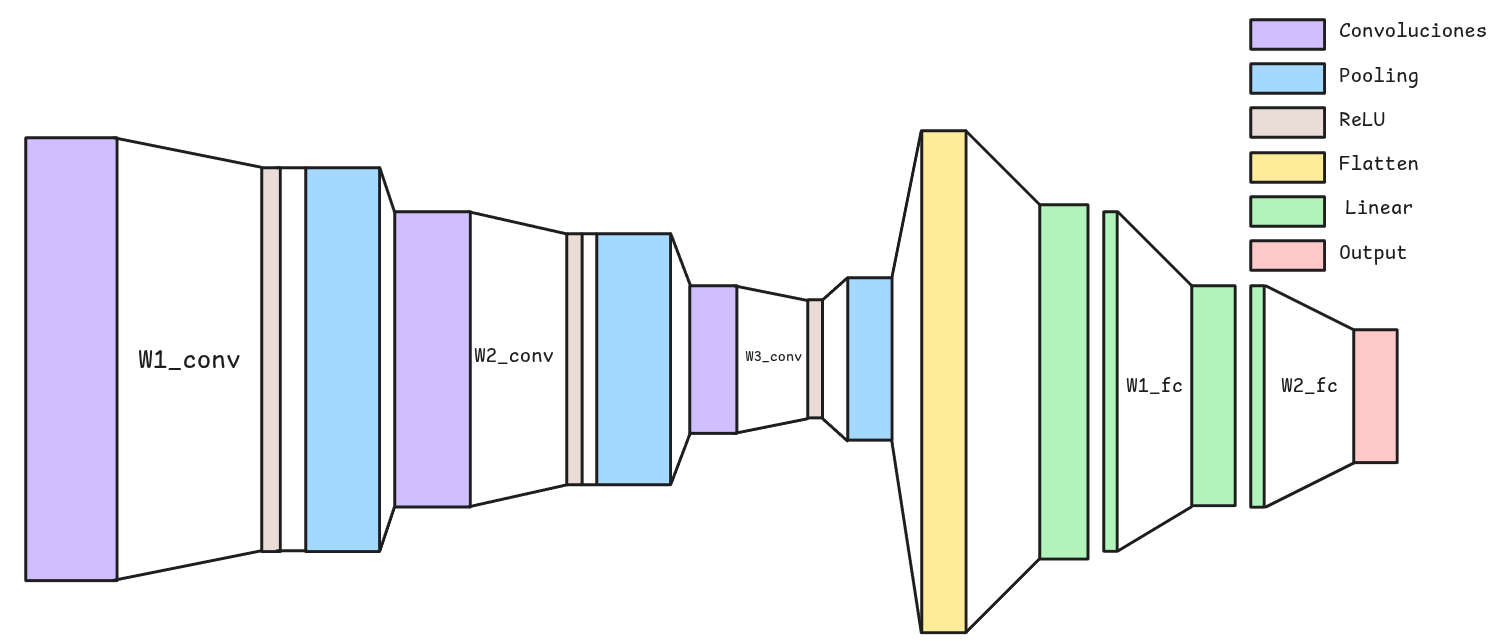
Architectura General

Una Convolutional Neural Network (CNN) está formada por múltiples capas que colaboran para identificar y extraer características significativas de las imágenes, con el fin de clasificarlas o detectar objetos dentro de ellas.

Feature Extractor - Encoder - Backbone

Corresponde al bloque en el que se detectan características o patrones relevantes de la imagen. En este bloque es donde se aplican normalmente las operaciones de Convolución y Pooling.

Flatten

Corresponde a una operación intermedia que aplana los feature maps generadas para ser utilizados como features de entrada para ser utilizados por la parte final de la red.

Prediction Head - Head - MLP

Corresponde a una FFN que tomará las features aprendidas por la CNN y generará una predicción.

La Convolución

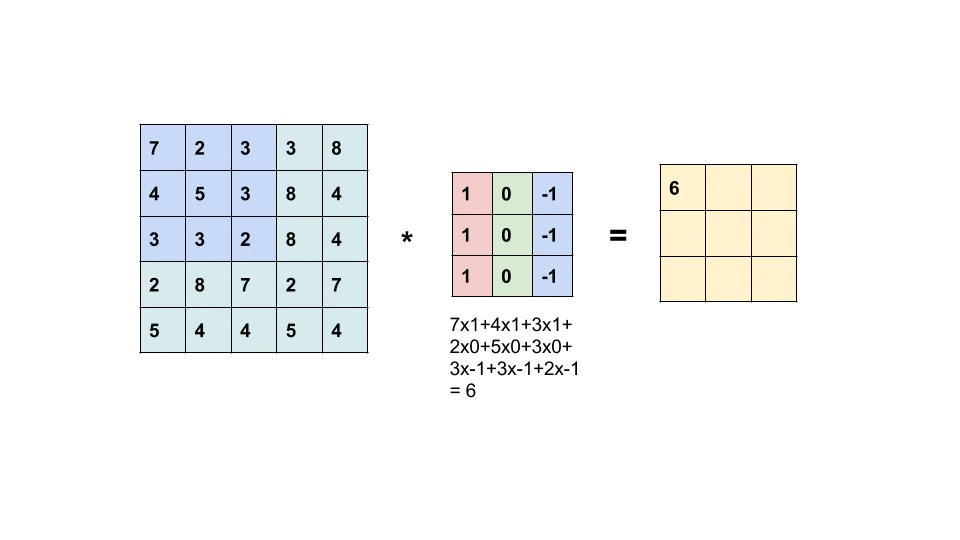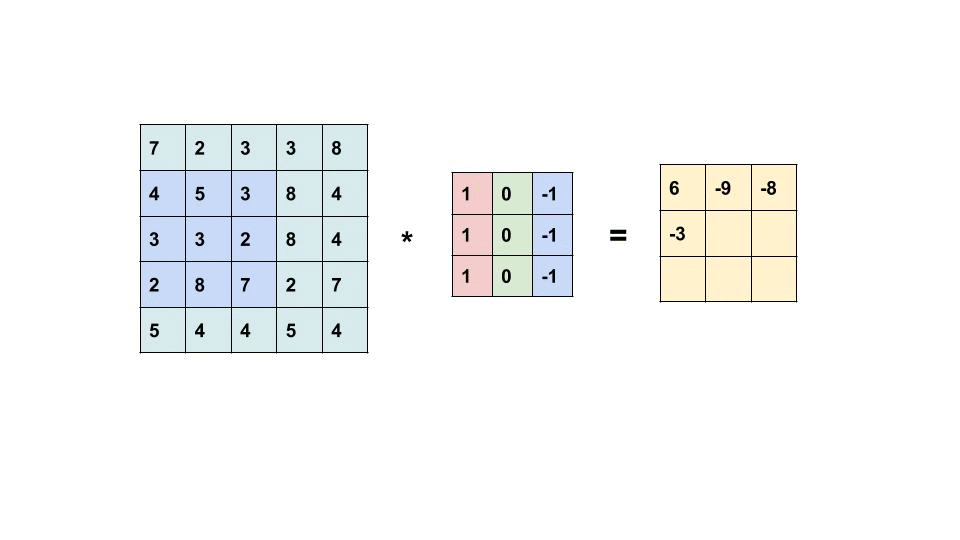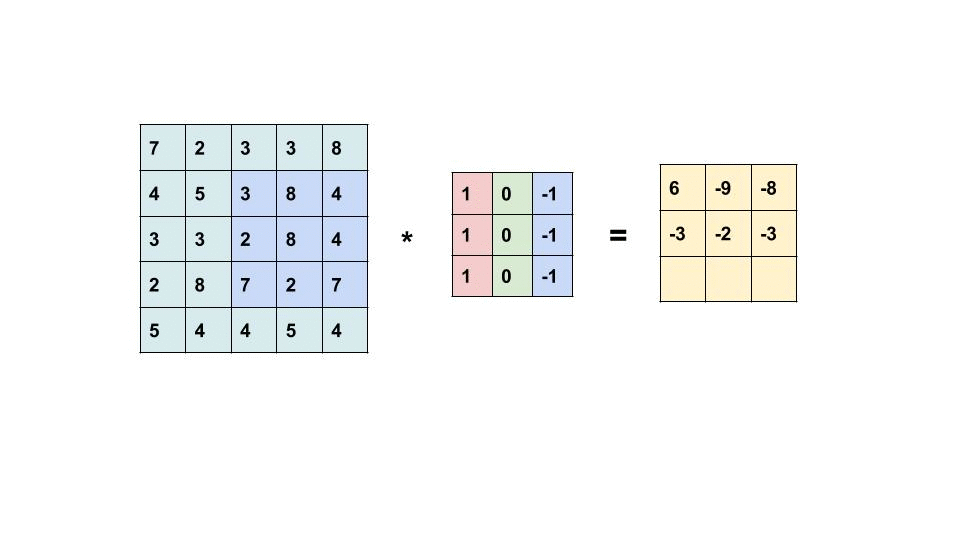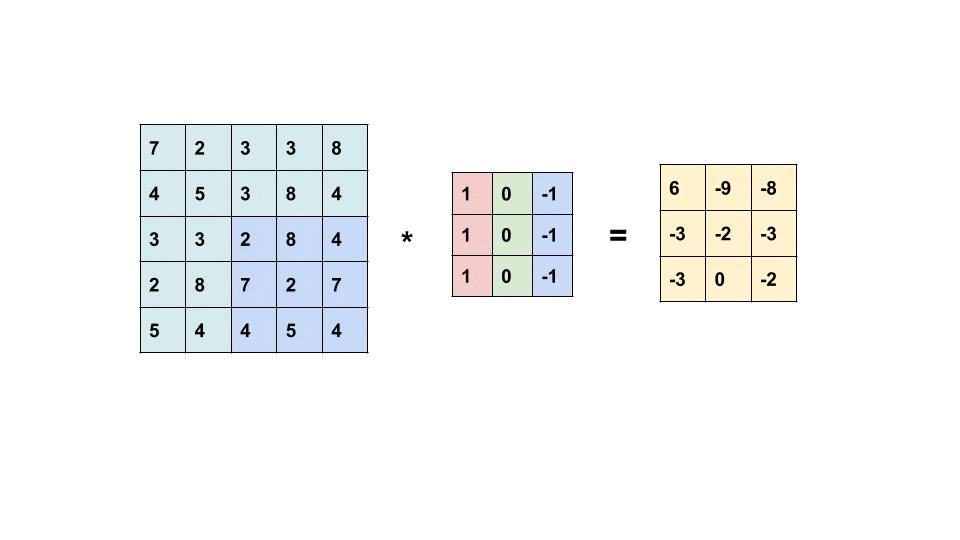
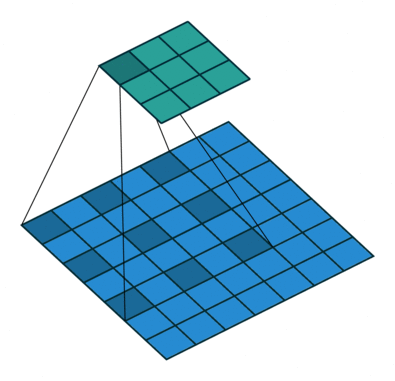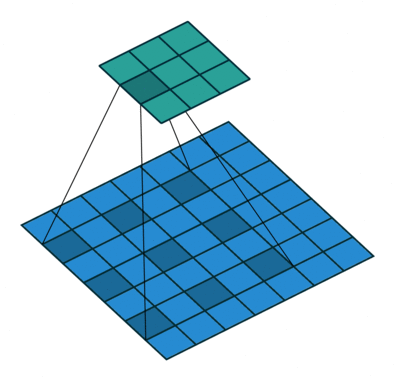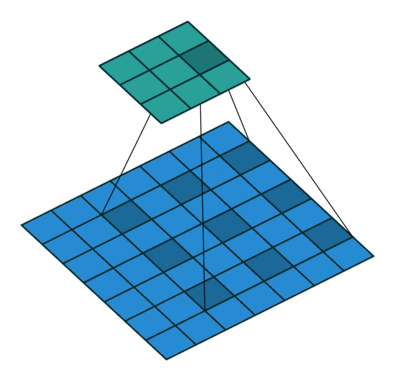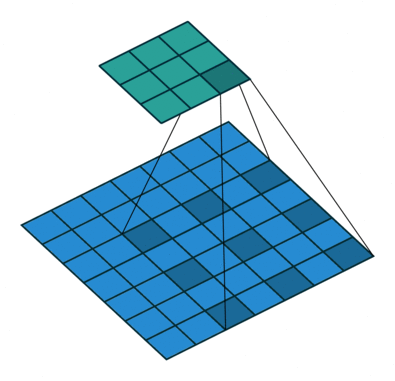
Convolución: Corresponde a una operación que permite extraer feature maps, donde un filtro o kernel se desplaza sobre distintas secciones de los datos, ya sea una secuencia, una imagen o un video, para capturar sus patrones más relevantes.

☝️Atención

Esto es nuevamente un término marketero, porque no es una Convolucional real, sino una operación llamada Cross Correlation.

Feature Map: Corresponde a la salida de una convolución (equivalente a la Activación) y es un nuevo tensor que captura ciertas características del dato (secuencia, imagen o video). Cuando se trata de imágenes, captura features como bordes, cambios de textura, color, formas, o elementos más pequeños.

Es importante notar que los features maps son de una tamaño menor a la entrada debido a la operación de Convolución.

Se obtendrán tantos feature maps como filtros se apliquen. Esto es otro hiperparámetro de la Red Convolucional que se conoce como los canales de salida o out_channels.

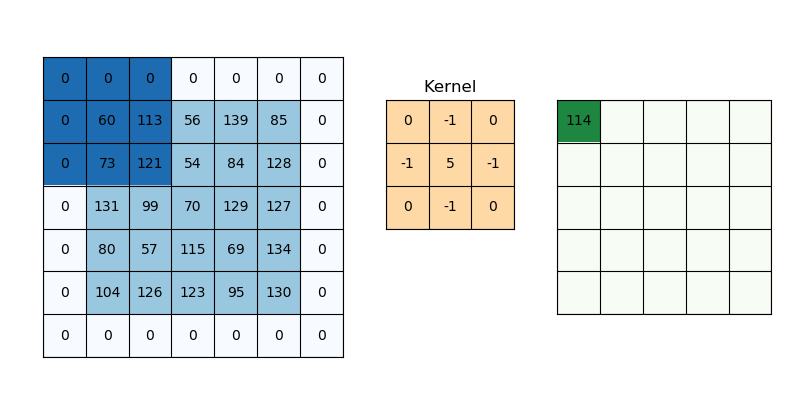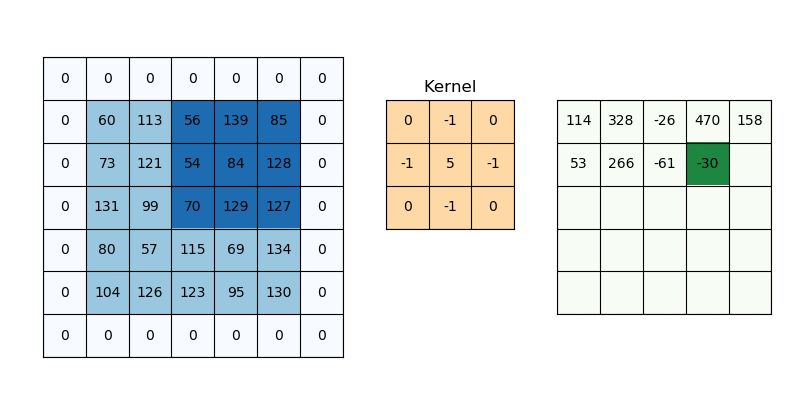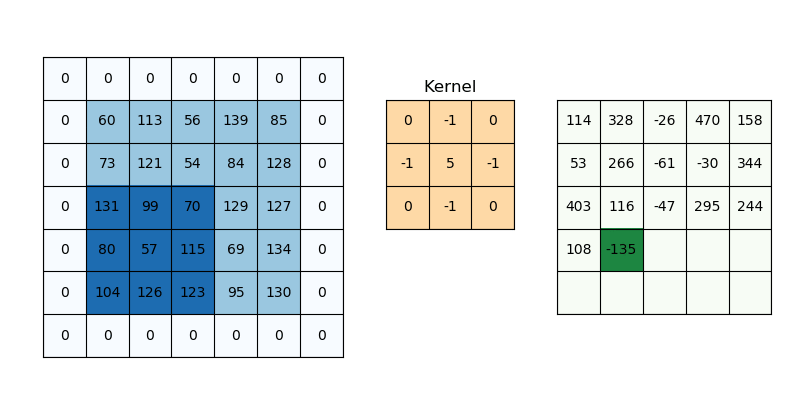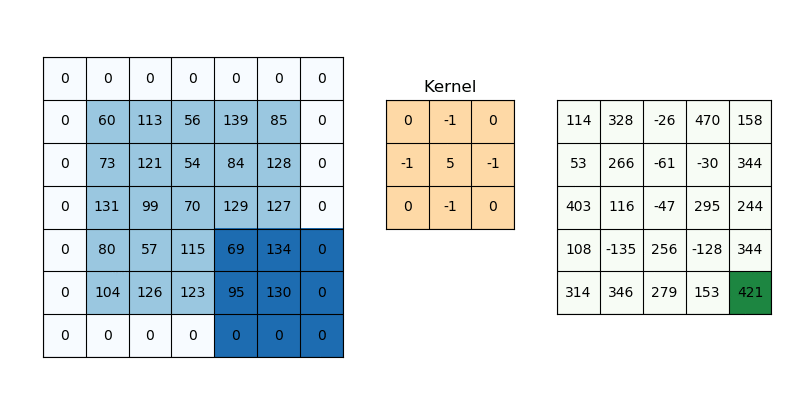
El filtro o Kernel

Gaussian Blur

Líneas Horizontales

Bordes

Kernel

Corresponde a una matriz pequeña que permite detectar patrones específicos en la imagen al aplicarse de manera móvil sobre ella. Estos Kernel solías estudiarse y diseñarse manualmente para tareas específicas como detección de bordes, desenfoque, realce de contraste, entre otros.

En una red convolucional, el kernel es un conjunto de pesos que se ajustan durante el proceso de entrenamiento para identificar características relevantes en las imágenes. Es decir, la CNN aprende qué Kernels son más importantes para la tarea que se está resolviendo.

El Kernel se aplica a todos los canales a la vez, lo cuál inicialmente lo hace ver como una operación bastante costosa computacionalmente.

El Kernel introduce el primer hiperparámetro de las CNN que es el Kernel Size. En general son cuadrados, y de dimensión impar.

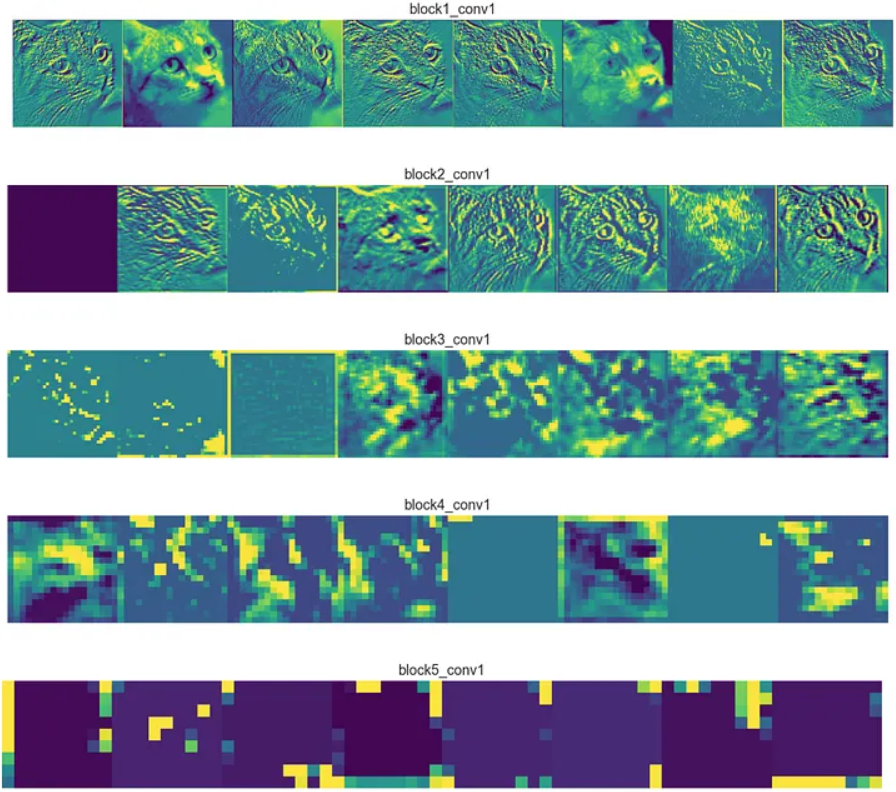
Feature Maps

Feature Map: Corresponde a la salida de una convolución (equivalente a la Activación) y es un nuevo tensor que captura ciertas características del dato (secuencia, imagen o video). Cuando se trata de imágenes, captura features como bordes, cambios de textura, color, formas, o elementos más pequeños.

Básicamente los feature maps son imágenes que resaltan ciertos patrones aprendidos por los kernels.

A medida que avanzamos en las capas convolucionales, los feature maps tienden a capturar patrones más complejos y abstractos.

Cada feature map es de tamaño más pequeño que la imagen original, pero contiene información más relevante para la tarea de clasificación o detección.

Se obtendrán tantos feature maps como filtros se apliquen. Esto es otro hiperparámetro de la Red Convolucional que se conoce como los canales de salida o out_channels.

Hiperparámetros de la Convolución

Stride

Hace referencia al número de posiciones que el kernel se desplaza sobre la imagen de entrada en cada paso. Un stride más grande produce feature maps más pequeños y con menos detalle, mientras que un stride más pequeño preserva mayor información, aunque incrementa la cantidad de operaciones necesarias.

Padding

Consiste en añadir un relleno alrededor de la imagen de entrada para facilitar el desplazamiento del kernel y evitar que la convolución reduzca en exceso sus dimensiones. Este relleno también permite conservar la información presente en los bordes de la imagen. Cuando no se aplica padding, la operación se denomina “valid”, mientras que si se agregan los píxeles necesarios para mantener el tamaño original, se conoce como “same”.

Dilation

Hace referencia a los espacios o intervalos que se insertan entre los elementos del kernel durante la convolución. El uso de dilation permite ampliar el campo receptivo de la red, capturando un mayor contexto sin aumentar el tamaño del kernel. Un valor de 1 indica que no se aplica dilation.

Convolución en Pytorch

nn.Conv2d(in_channels, out_channels, kernel_size, stride=1,padding=0,dilation=1)

Input

Este tipo de redes no requiere que se le den las dimensiones de las entradas, pero sí espera recibir tensores de dimensión \((N,C_{in}, H_{in},W_{in})\).

Output

La Red convolucional devuelve un Tensor de Dimensiones \((N,C_{out}, H_{out}, W_{out})\). Donde:

\[H_{out} = \left\lfloor \frac{H_{in} + 2 \cdot padding[0] - dilation[0]\cdot (kernel\_size[0] - 1) - 1}{stride[0]} + 1 \right\rfloor\] \[W_{out} = \left\lfloor \frac{W_{in} + 2 \cdot padding[1] - dilation[1]\cdot (kernel\_size[1] - 1) - 1}{stride[1]} + 1 \right\rfloor\]

Es importante tener noción del tamaño de la imagen para poder escoger un kernel_size que recorra la imagen completa y que no deje partes sin convolucionar.

Partes de una CNN: Pooling

Pooling: El Pooling es una operación de agregación que permite ir disminuyendo el tamaño de las entradas. De esta manera la red puede comenzar a especializarse en aspectos cada vez más finos.

El Pooling también se aplica de manera móvil como una convolución. Pero a diferencia de esta normalmente no genera traslape.

Acá se introduce otro hiperparámetro que es el Pooling Size. En general es cuadrado y de dimensión par, y utiliza un stride del mismo tamaño que el Pooling Size para evitar traslapes.

Pooling in Pytorch

nn.AvgPool2d(kernel_size, stride=None,padding=0)
nn.MaxPool2d(kernel_size, stride=None,padding=0, dilation=1)

Ojo

Pytorch llama también kernel_size al tamaño del Pooling.
stride=None implica stride = kernel_size.

MaxPool

AvgPool

\[H_{out} = \left\lfloor \frac{H_{in} + 2 \cdot padding[0] - kernel\_size[0]}{stride[0]} + 1 \right\rfloor\] \[W_{out} = \left\lfloor \frac{W_{in} + 2 \cdot padding[1] - kernel\_size[1]}{stride[1]} + 1 \right\rfloor\]

El Average Pool no permite Dilation.

AdaptivePooling

La mayoría de las arquitecturas CNN modernas aplican un procedimiento llamado Adaptive Pooling antes de la etapa de predicción (FFN). Independientemente del tamaño de la imagen de entrada, el Adaptive Pooling siempre genera una salida de tamaño fijo, ya que ajusta sus parámetros para asegurar que la dimensión de salida sea la deseada.

nn.AdaptiveAvgPool2d(output_size)
nn.AdaptiveMaxPool2d(output_size, return_indices=False)

return_indices=True permite devolver en qué posiciones se encontraron los valores máximos, lo cual es útil para operaciones de unpooling para revertir el proceso de pooling.

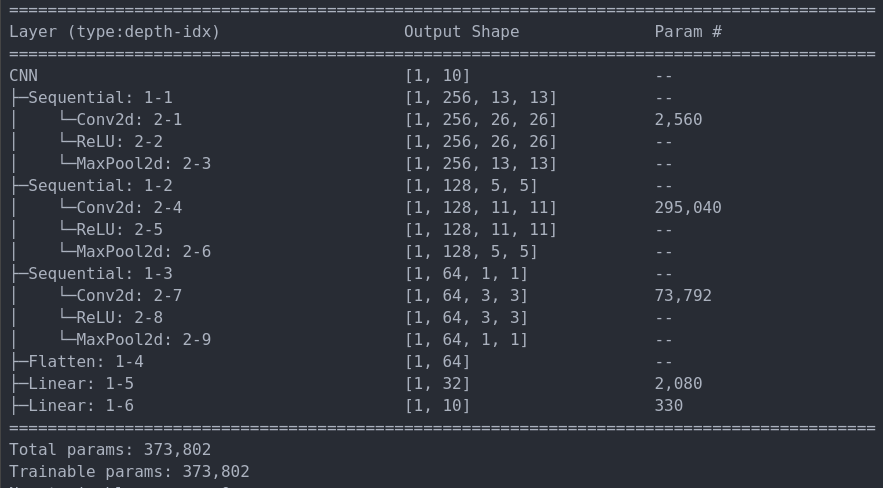
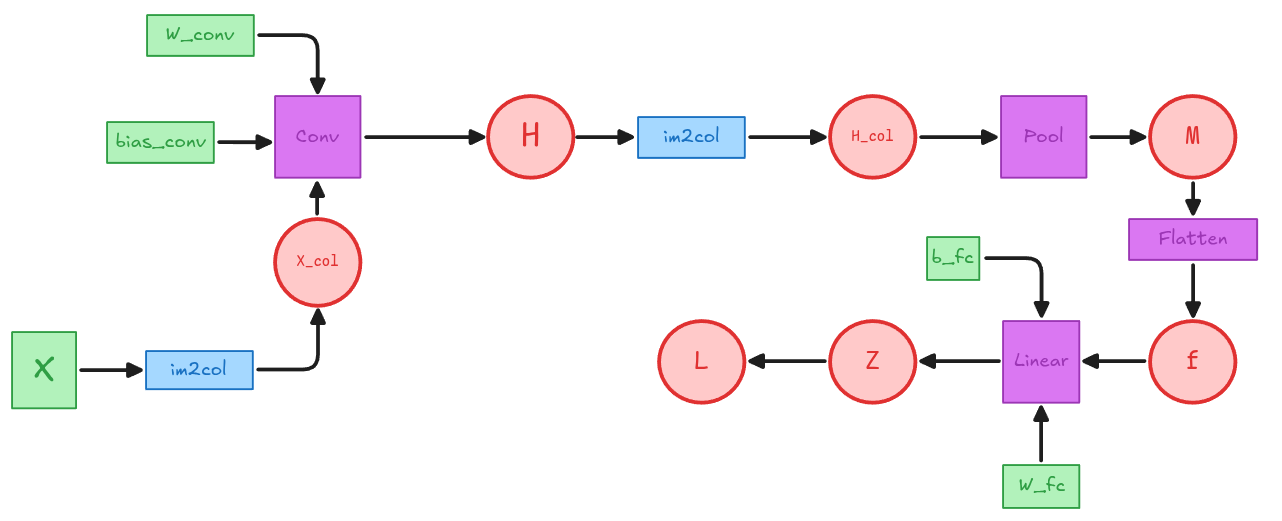
MNIST con CNN

El número de Parámetros para una Red Convolucional con muchas más capas bajó considerablemente, de 67M a 373K de Parámetros para una imagen de \(512 \times 512\).

Grafo CNN sencilla

## Una Imagen de 1 Canal de Tamaño 6x6
X = torch.tensor([
        [[[7., 6., 8., 5., 1., 3.],
          [8., 6., 5., 3., 5., 5.],
          [9., 1., 1., 5., 3., 5.],
          [4., 5., 5., 9., 2., 6.],
          [9., 5., 3., 1., 2., 2.],
          [4., 4., 8., 8., 9., 8.]]]
])
X.shape

(1,1,6,6)

C_out = 2
N, C_in, H, W = X.shape
kH, kW = (3,3)

## 2 filtros de un Canal de tamaño 3x3
given_w = torch.tensor([
        [[[1.,  1.,  0.],
          [ -1., 1.,  -1.],
          [ 0.,  -1.,  -1.]]],

        [[[1., 1.,  0.],
          [-1.,  1.,  -1.],
          [ -1.,  0.,  -1.]]]])
given_w.shape

(2,1,3,3)

given_bias = torch.tensor([1., 1.])

Grafo CNN sencilla: Convolución

def calculate_out(X, k_size=(3,3), stride=1, dilation=1, padding=0):
  kH, kW = k_size
  N, in_channels, H_in, W_in = X.shape
  out_H = np.floor((H_in +2*padding-dilation*(kH-1)-1)/stride + 1)
  out_W = np.floor((W_in +2*padding-dilation*(kW-1)-1)/stride + 1)
  return int(out_H), int(out_W)

H_out, W_out = calculate_out(X, k_size = (kH,kW))
H_out, W_out

(4,4)

O = torch.zeros((N, C_out, H_out, W_out))
for n in range(N):
    for co in range(C_out):
        for i in range(H_out):
            for j in range(W_out):
                # submatriz de tamaño kH x kW
                patch = X[n, :, i:i+kH, j:j+kW]
                O[n, co, i, j] = (patch * given_w[co]).sum() + given_bias[co]
O

tensor([[[[  5.,   5.,  -1.,  -4.],
          [ -4.,  -7.,  -1.,  -6.],
          [ -1., -10.,   6.,  -8.],
          [ -9.,  -8.,  -6.,  -6.]],

         [[ -3.,   5.,   3.,  -6.],
          [ -3.,  -7.,   3., -13.],
          [ -5., -12.,   4.,  -7.],
          [ -9.,  -4.,  -6.,  -5.]]]])

Este proceso es extremadamente ineficiente computacionalmente hablando. Por lo que se utiliza un proceso equivalente llamado im2col.

im2col

im2col es un algoritmo que permite transformar la operación de convolución en una operación de multiplicación de matrices, lo cual es computacionalmente más eficiente. En este caso los parches que requieren la convolución se aplanan y se organizan en columnas de una nueva matriz.

El procedimiento en Pytorch se realiza de la siguiente manera:

## Cada columna es un patche aplanado de 3x3. 16 patches en total.
X_col = F.unfold(X, kernel_size=(kH, kW))  # (1, 9, 16) (N,kH*kW,n_patches)
print(f"X_col shape: {X_col.shape}")
X_col

X_col shape: torch.Size([1, 9, 16])
tensor([[[7., 6., 8., 5., 8., 6., 5., 3., 9., 1., 1., 5., 4., 5., 5., 9.],
         [6., 8., 5., 1., 6., 5., 3., 5., 1., 1., 5., 3., 5., 5., 9., 2.],
         [8., 5., 1., 3., 5., 3., 5., 5., 1., 5., 3., 5., 5., 9., 2., 6.],
         [8., 6., 5., 3., 9., 1., 1., 5., 4., 5., 5., 9., 9., 5., 3., 1.],
         [6., 5., 3., 5., 1., 1., 5., 3., 5., 5., 9., 2., 5., 3., 1., 2.],
         [5., 3., 5., 5., 1., 5., 3., 5., 5., 9., 2., 6., 3., 1., 2., 2.],
         [9., 1., 1., 5., 4., 5., 5., 9., 9., 5., 3., 1., 4., 4., 8., 8.],
         [1., 1., 5., 3., 5., 5., 9., 2., 5., 3., 1., 2., 4., 8., 8., 9.],
         [1., 5., 3., 5., 5., 9., 2., 6., 3., 1., 2., 2., 8., 8., 9., 8.]]])

im2col

¿Qué pasa si ahora aplanamos los filtros también?

## Dejamos cada filtro como una fila
W_row = given_w.reshape(C_out, -1)
print(W_row.shape)
W_row

(2,9)
tensor([[ 1.,  1.,  0., -1.,  1., -1.,  0., -1., -1.],
        [ 1.,  1.,  0., -1.,  1., -1., -1.,  0., -1.]])

💭 Luego La convolución se puede pensar como una transformación lineal aplicada a parches aplanados de la imagen de entrada. Es decir cada parches es transformado linealmente por los filtros aplanados, generando una nueva representación de la imagen (un feature map).

Entonces podemos expresar la convolución como una multiplicación de matrices muy similar a una FFN:

\[H_{col} = W_{row} \cdot X_{col} + b \cdot 1_{C_{in}*kH*KW}^T \]

Donde \(b\) tiene dimensiones \(C_{out} \times 1\) y \(1^T_{C_{in}*kH*kW}\) tiene dimensiones \(1 \times C_{in}*kH*kW\). Aunque es más sencillo pensar el \(b\) como un vector que se le aplica Broadcasting.

Luego para volver a la forma de la imagen basta con hacer un reshape:

H = H_col.reshape(N, C_out, H_out, W_out)
print(H.shape)
H

(1, 2, 4, 4)

tensor([[[[  5.,   5.,  -1.,  -4.],
          [ -4.,  -7.,  -1.,  -6.],
          [ -1., -10.,   6.,  -8.],
          [ -9.,  -8.,  -6.,  -6.]],

         [[ -3.,   5.,   3.,  -6.],
          [ -3.,  -7.,   3., -13.],
          [ -5., -12.,   4.,  -7.],
          [ -9.,  -4.,  -6.,  -5.]]]])

Pooling

Nuevamente necesitamos hacer un `im2col` para poder hacer el pooling como una multiplicación de matrices.

Eso implica que H quedará como:

pool_size = 2
H_pool, W_pool = calculate_out(H, k_size=(2,2),stride=2) 
## (2,2)
h_col = F.unfold(H, kernel_size=pool_size, stride=pool_size)
print(h_col.shape)
h_col

(1,8,4)
tensor([[[  5.,  -1.,  -1.,   6.],
         [  5.,  -4., -10.,  -8.],
         [ -4.,  -1.,  -9.,  -6.],
         [ -7.,  -6.,  -8.,  -6.],
         [ -3.,   3.,  -5.,   4.],
         [  5.,  -6., -12.,  -7.],
         [ -3.,   3.,  -9.,  -6.],
         [ -7., -13.,  -4.,  -5.]]])

😱Notar como la operación de im2col genera parches para todos los canales a la vez. Por lo tanto es necesario separar por canales para aplicar el pooling.

## Tenemos 2 canales de 4 por cada uno
## al cuál debemos aplicar el máximo.
h_col_reshaped = h_col.reshape(N, C_out, pool_size*pool_size, -1)
h_col_reshaped

(1,2,4,4)
tensor([[[[  5.,  -1.,  -1.,   6.],
          [  5.,  -4., -10.,  -8.],
          [ -4.,  -1.,  -9.,  -6.],
          [ -7.,  -6.,  -8.,  -6.]],

         [[ -3.,   3.,  -5.,   4.],
          [  5.,  -6., -12.,  -7.],
          [ -3.,   3.,  -9.,  -6.],
          [ -7., -13.,  -4.,  -5.]]]])

## Calculamos el máximo de cada columna (que es un parche de 2x2)
## Además guardamos la posición del máximo
M_flat, pool_indices = h_col_reshaped.max(dim=2)
M_flat

tensor([[[ 5., -1., -1.,  6.],
         [ 5.,  3., -4.,  4.]]])

## Recuperamos la forma del feature map luego del pooling
M = M_flat.reshape(N, C_out, H_pool, W_pool)
print(M.shape)
M

(1,2,2,2)
tensor([[[[ 5., -1.],
          [-1.,  6.]],

         [[ 5.,  3.],
          [-4.,  4.]]]])

Flatten y FFN

f = M.reshape(N, -1)
print(f.shape)

tensor([[ 5., -1., -1.,  6.,  5.,  3., -4.,  4.]])

Z = f @ W_fc + b_fc
Z

tensor([[18.]])

Utilizando `nn.Module`

class Conv(nn.Module):
  def __init__(self):
      super().__init__()
      self.conv = nn.Conv2d(in_channels=1, out_channels=2, kernel_size=3, bias=True)
      self.conv.weight.data = given_w
      self.conv.bias.data = given_bias
      self.max_pool = nn.MaxPool2d(kernel_size=2, return_indices=True)
      self.fc = nn.Linear(8, 1)
      nn.init.ones_(self.fc.weight)
      nn.init.ones_(self.fc.bias)
      self.flatten = nn.Flatten()

  def forward(self, x):
      x = self.conv(x)
      x, self.indices = self.max_pool(x)
      x = self.flatten(x)
      x = self.fc(x)
      return x

model = Conv()
# Forward con PyTorch
logits = model(X)

tensor([[18.]])

# Linear
W_fc = torch.ones(8, 1)

tensor([[1.],
        [1.],
        [1.],
        [1.],
        [1.],
        [1.],
        [1.],
        [1.]])

b_fc = torch.ones(1)

tensor([1.])

¿Le interesa calcular los gradientes?

Calcular los gradientes de una CNN se simplifica bastante utilizando el enfoque de im2col, ya que la convolución se ha transformado en una multiplicación de matrices. Esto permite aplicar los conceptos que aprendimos en la primera parte del curso.

Aún así aparecen conceptos que escapan del conocimiento del Cálculo que conocemos, como por ejemplo el Gradiente del im2col (que Spoiler, es el algoritmo col2im).

Échele una miradita al notebook de la clase, hay muchas horas de esfuerzo invertidas ahí.

Variante en 1d

Conv1d: Corresponde a la variante de una dimensión, en la cual la entrada corresponden a secuencias de elementos como podrían ser series de tiempo, audio o hasta cadenas de texto.

En este caso la implementación en Pytorch es similar a la 2D sólo que esperando tensores de dimensiones \((N,C_{in}, L_{in})\), donde \(C_{in}\) corresponde al número de canales, que en el caso de series de tiempo equivale a features, y \(L_{in}\) corresponde al largo de la secuencia.

La salida de la Conv1d tendrá dimensiones \((N,C_{out},L_{out})\) con:

\[L_{out} = \left\lfloor \frac{L_{in} + 2 \cdot padding - dilation \cdot (kernel\_size - 1) - 1}{stride} + 1 \right\rfloor\]

Variante en 3d

Conv3d: Corresponde a la variante de tres dimensiones, en la cual la entrada corresponde a secuencias de imágenes, es decir, videos.

Este caso también es similar sólo que se esperan tensores de dimensiones \((N, C_{in}, D_{in}, H_{in}, W_{in})\) donde \(C_in\) corresponde al número de canales, \(D\) en el caso de un video corresponde al número de frames de tamaño \(H_{in} \times W_{in}\).

La salida de la Conv1d tendrá dimensiones \((N,C_{out},D_{out},H_{out},W_{out})\) con:

\[D_{out} = \left\lfloor \frac{D_{in} + 2 \cdot padding[0] - dilation[0] \cdot (kernel\_size[0] - 1) - 1}{stride[0]} + 1 \right\rfloor\] \[H_{out} = \left\lfloor \frac{H_{in} + 2 \cdot padding[1] - dilation[1]\cdot (kernel\_size[1] - 1) - 1}{stride[1]} + 1 \right\rfloor\] \[W_{out} = \left\lfloor \frac{W_{in} + 2 \cdot padding[2] - dilation[2]\cdot (kernel\_size[2] - 1) - 1}{stride[2]} + 1 \right\rfloor\]

TICS-579-Deep Learning

Limitaciones de las FFN

Número de Parametros

(Imagen: 28x28=784 píxeles):

Limitaciones de las FFN

Limitaciones de las FFN

Imagenes actuales cada vez más grandes

Textos actuales cada vez más largos

Imágenes

Imágenes

Ejemplo para importar imágenes con PIL y Pytorch

Batch de Imágenes

Redes Convolucionales: Definición e Inspiración

Redes Convolucionales: Definición e Inspiración

🗓️ Algunos hitos importantes:

Convolutional Neural Network (CNNs)

La Convolución

El filtro o Kernel

Gaussian Blur

Líneas Horizontales

Bordes

Feature Maps

Hiperparámetros de la Convolución

Convolución en Pytorch

Partes de una CNN: Pooling

Pooling in Pytorch

AdaptivePooling

MNIST con CNN

Grafo CNN sencilla

Grafo CNN sencilla: Convolución

im2col

im2col

Pooling

Nuevamente necesitamos hacer un im2col para poder hacer el pooling como una multiplicación de matrices.

Eso implica que H quedará como:

Flatten y FFN

Utilizando nn.Module

¿Le interesa calcular los gradientes?

Variante en 1d

Variante en 3d

🥵 Terminamos

Nuevamente necesitamos hacer un `im2col` para poder hacer el pooling como una multiplicación de matrices.

Utilizando `nn.Module`