TICS-579-Deep Learning

Clase 8: Redes Recurrentes

Alfonso Tobar-Arancibia

alfonso.tobar.a@edu.uai.cl

Datos Secuenciales

Hasta ahora, hemos asumido que los datos con los que trabajamos son independientes e idénticamente distribuidos (i.i.d). Sin embargo, en muchos casos, los datos tienen una estructura secuencial que debe ser considerada al momento de modelarlos. Algunos ejemplos comunes de datos secuenciales incluyen:

Time Series (precios de acciones, datos meteorológicos, etc)

Audio (grabaciones de voz, música, etc)

Texto (oraciones, documentos, etc)

Genoma (secuencias de ADN, etc.)

Datos Secuenciales

También pudiesen existir datos “multimodales”, donde por ejemplo, se combinan secuencias con imágenes.

Image Time Series

Video

¿Cómo se ven datos secuenciales reales?

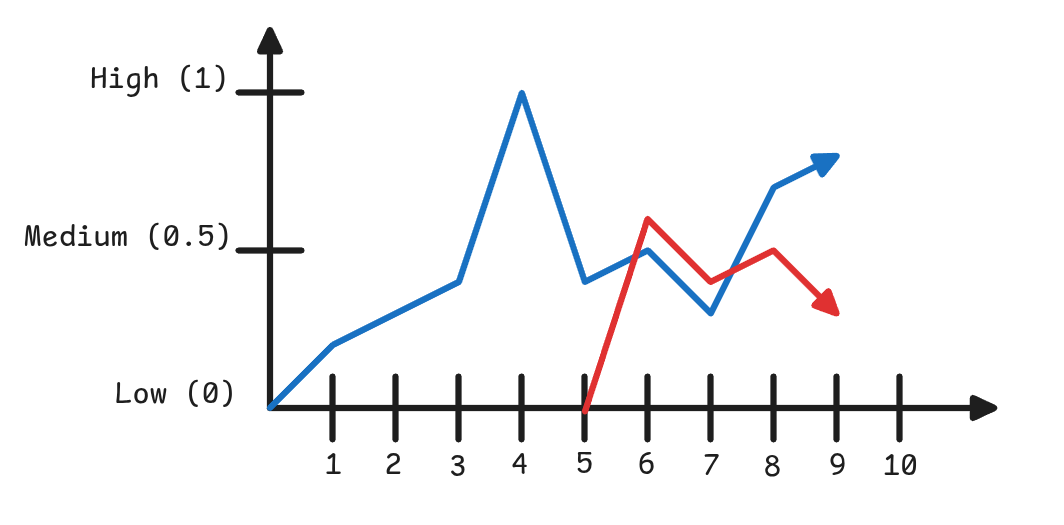
Supongamos el siguiente ejemplo:

Buscamos predecir el porcentaje de retorno de la inversión en función de los retornos obtenidos en días anteriores.
En este ejemplo, la acción “Azul” cuenta con un historial de 10 días, mientras que la acción “Roja” dispone únicamente de 5 días de historial.

Nos gustaría poder entrenar un modelo capaz de trabajar con datos de entrada de distintas longitudes (secuencias de tamaño variable).

Queremos que el modelo sea capaz de utilizar información pasada para realizar predicciones sobre valores futuros.

Redes Neuronales Recurrentes (RNNs)

RNN: Corresponden a un tipo de red neuronal diseñada para procesar secuencias de datos manteniendo en memoria los inputs previos. A diferencia de los otros tipos de redes que procesan datos de manera independiente, acá existen conexiones cíclicas que permiten retener información en el tiempo.

\[h_t = f(x_t \cdot W_{ih}^T + b_{ih} + h_{t-1} \cdot W_{hh}^T + b_{hh})\]

En la implementación original $f$ corresponde a la $tanh(\cdot)$.

Recurrent Neural Networks

Pros

Pueden tomar secuencias de distinto tamaño (Largo) como predictores de un problema.
Toman como antecedentes los puntos pasados como referencia para las predicciones futuras.

Cons

Se van complicando a medida que las secuencias son cada vez más largas.
Vanishing/Exploding Gradients Problem.

Nomenclatura

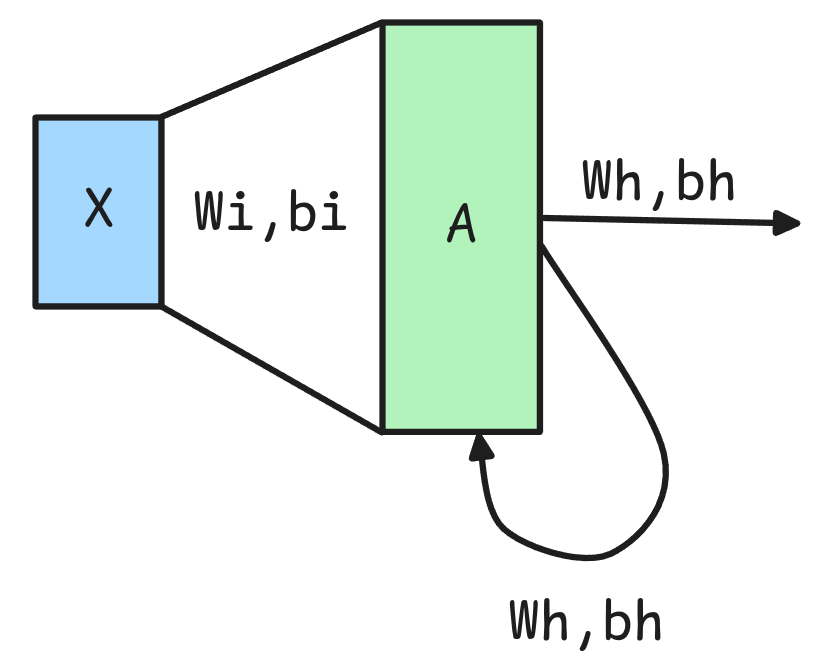
A las salidas de una RNN se les suele llamar Hidden State ($h_t$) o Estado Oculto. Este representa la memoria de la red en el tiempo $t$.

🚨 Una RNN tiene dos set de parámetros: $W_{ih}$ y $b_{ih}$, los cuales representan la transformación entre los valores de entrada y el estado oculto, y $W_{hh}$ y $b_{hh}$ los que representan la transformación entre el estado oculto previo y el actual (Feedback Loop).

👀 Es importante mencionar que las RNN son aplicadas a la secuencia elemento a elemento.

Implementación Básica de una RNN

rnn = nn.RNN(input_size=1, hidden_size=2, num_layers=1, batch_first=True)

def forward_pass_rnn(x):
    N, L, D = x.shape 
    h=[0]
    for seq_id in range(L):
        h.append(torch.tanh(x[:,seq_id,:]*rnn.weight_ih_l0 + rnn.bias_ih_l0 + h[-1]*rnn.weight_hh_l0 + rnn.bias_hh_l0))
    return h

# Una secuencia de (3,1)
x1 = torch.tensor([[[2.],
                    [7.],
                    [6.]]])
forward_pass_rnn(x1)

tensor([[0.4727, 0.1731]],
        [[ 0.9106, -0.9335]],
        [[ 0.7067, -0.9780]])

Shape: (1,3,2)

# Una secuencia de (2,1)
x2 = torch.tensor([[[4.],
                    [6.]]]))
forward_pass_rnn(x2)

tensor([[ 0.6634, -0.4728]]),
        [[ 0.7876, -0.9505]])

Shape: (1,2,2)

🚨 Básicamente la RNN genera una transformación affine por cada time step $t$ agregando información de su memoria pasada. Es decir, cada elemento de la secuencia es transformado y llevado a un número de dimensiones igual a hidden_size.

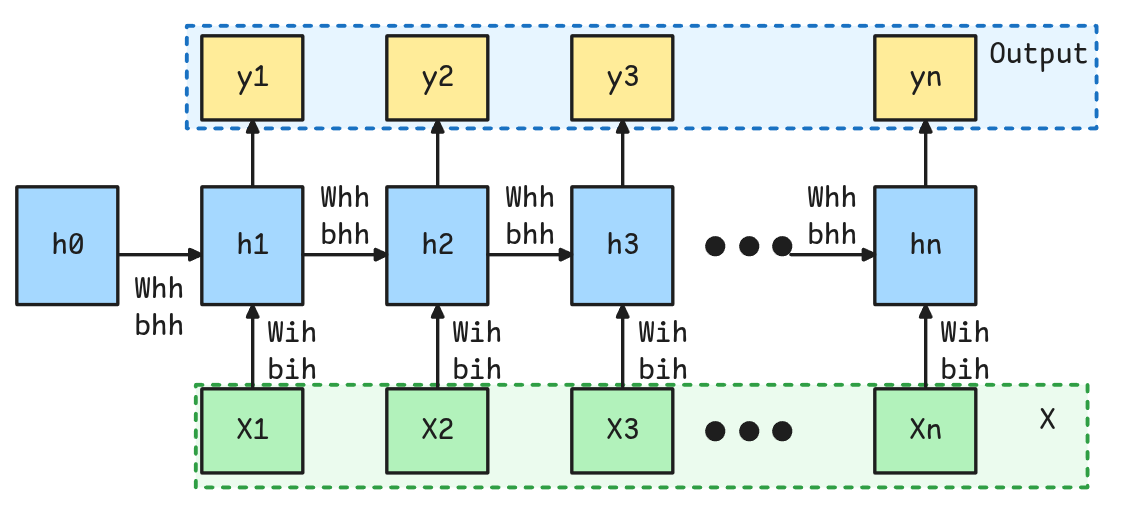
Unrolling RNN

☝️ Nomenclatura en Pytorch

El output $y_t$ tiene al mismo valor que $h_t$. Se utiliza nomenclatura distinta para diferenciar de una salida directa a un valor que será utilizado como input en el siguiente time step.
$h_0$ corresponde al hidden state inicial y tiene por defecto un vector de ceros.
$W_{ih}$ y $b_{ih}$ son los parámetros que proyectan la entrada $x_t$ al hidden size. Mientras que $W_{hh}$ y $b_{hh}$ son los parámetros que proyectan el hidden state previo $h_{t-1}$ al hidden state actual.

📢 Unrolling de una RNN

El unrolling consiste en representar una RNN como una secuencia virtual de capas conectadas que permite ver la relación entre los elementos de cada time step. Es importante notar que los parámetros se comparten, es decir, cada una de las capas tiene los mismos pesos y bias.

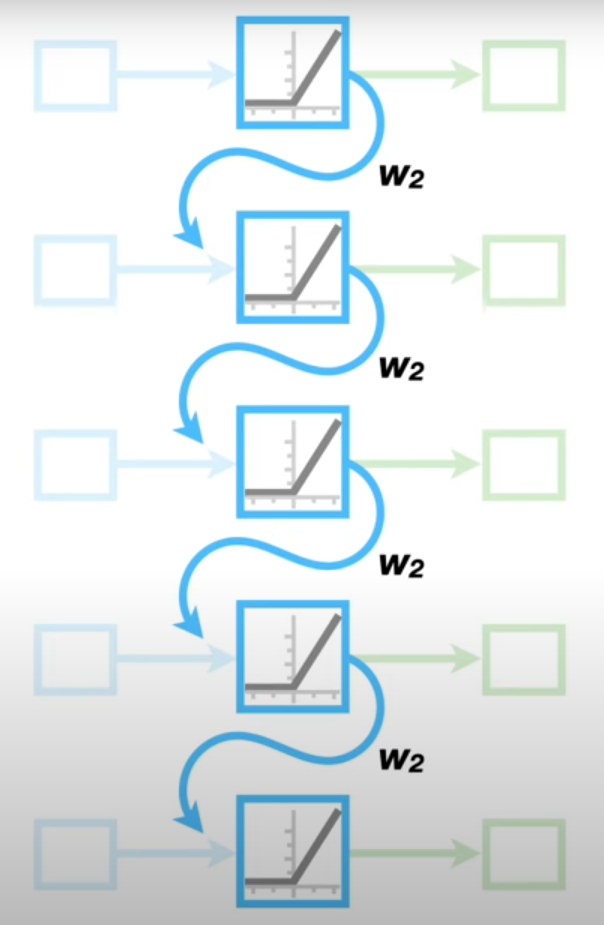
Vanishing/Exploding Gradients

Entre más larga se la secuencia (más unrolls se realicen), más difícil es entrenar la red debido a dos posibles problemas: el vanishing gradient problem y el exploding gradient problem.

\[Gradiente = f(Input \times W_2^{N_{Unroll}})\]

Cuando los valores de $W_2$ son muy pequeños (menores que 1), el gradiente tiende a desvanecerse (vanishing gradient).
En cambio, si los valores de $W_2$ son muy grandes (mayores que 1), el gradiente tiende a explotar (exploding gradient).

$W_2^{N_unroll} aparece en la ecuación al momento de comenzar a derivar de manera recursiva.

Las Vanilla RNNs se utilizan muy poco en la práctica; sin embargo, tienen una relevancia histórica significativa, ya que sentaron las bases para el desarrollo de arquitecturas más avanzadas, como las LSTMs y los Transformers.

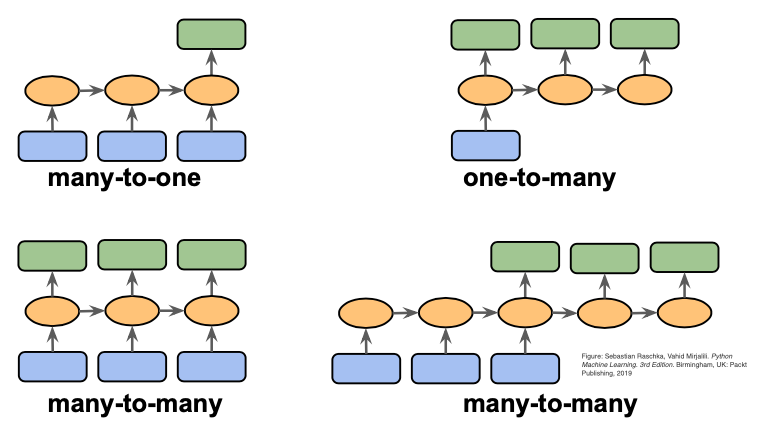
Tipos de Tareas a Resolver en Datos Secuenciales

🔔 Dependiendo de la Tarea de Interés esta se puede clasificar dependiendo de la cantidad de Inputs y la Cantidad de Output.

One to Many

Generación de Texto

Many to One

Sentiment Analysis
Time Series Forecasting
Time Series Classification

Many to Many

Part of Speech Tagging
Machine Translation

Algunos Ejemplos de Arquitecturas

✨✨ Part of Speech Tagging: Entrego una Secuencia de Largo L y obtengo una Secuencia de Largo L con Clases Asociadas.

class POSTaggingRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        rnn_out, hn = self.rnn(x)
        print("Tamaño del Output de RNN: ", hn.shape)
        logits = self.fc(rnn_out)
        return logits


model = POSTaggingRNN(input_size=1,
                    hidden_size=4,
                    output_size=3)
output = model(x1)
print("Shape del Output Final: ", output.shape)
output

Tamaño del Output de RNN:  torch.Size([1, 1, 4])
Shape del Output Final:  torch.Size([1, 3, 3])
tensor([[[-0.6526,  0.2722,  0.2755],
         [-1.1120,  0.7727,  0.4798],
         [-1.0416,  0.7447,  0.4793]]])

✨✨ Sentiment Analysis: Entrego una Secuencia de Largo L y obtengo una Clase Final (Positiva, Negativa, Neutra).

class SentimentAnalysisRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        rnn_out, hn = self.rnn(x)
        print("Tamaño del Hidden State del RNN: ", hn.shape)
        logits = self.fc(hn)
        return logits


model = SentimentAnalysisRNN(input_size=1, 
                            hidden_size=4,
                            output_size=3)
output = torch.softmax(model(x1), dim=-1)
print("Shape del Output Final: ", output.shape)
output

Tamaño del Hidden State del RNN:  torch.Size([1, 1, 4])
Shape del Output Final:  torch.Size([1, 1, 3])
tensor([[[0.0866, 0.5169, 0.3965]]])

Stacking RNNs

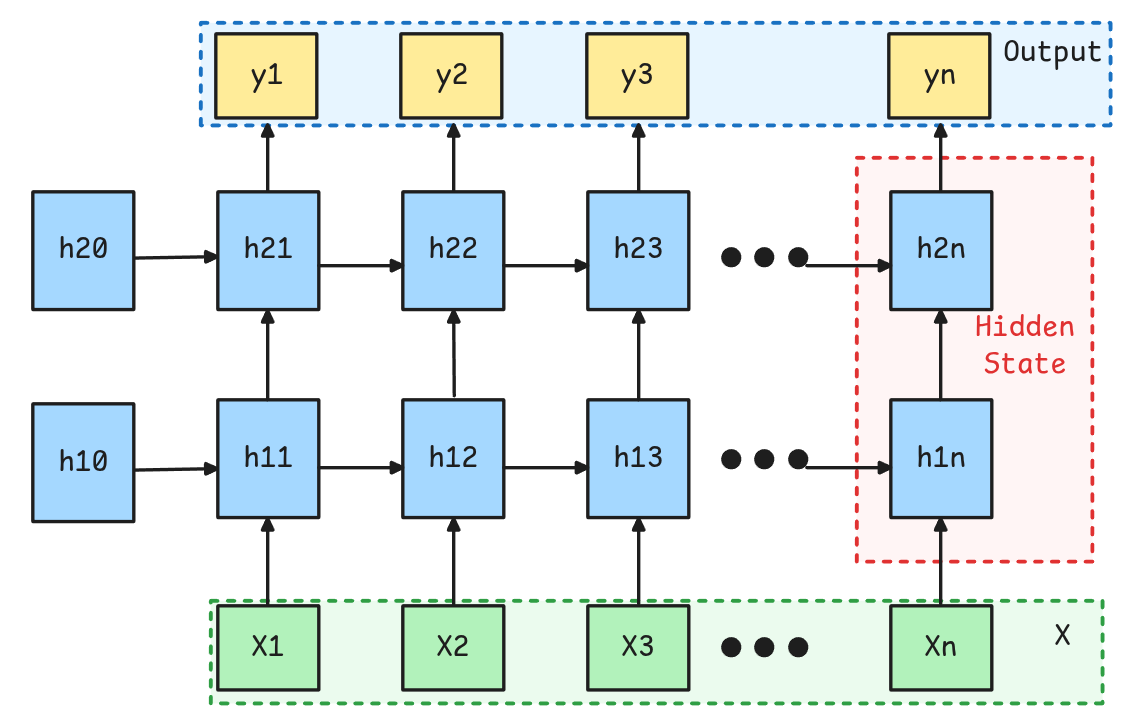
Es posible juntar varias capas recurrentes, para que las salidas de una alimenten un siguiente Hidden State, y que luego de algunas capas efectivamente se llegue a las salidas de interés.

Debido a que hacer esto es complicado esto viene integrado en la implementación en Pytorch mediante el parámetro num_layers.

OJO

No existen salidas intermedias, sino que los Hidden States de capas anteriores son utilizados directamente como inputs de los hidden states posteriores.

En Pytorch los Hidden States se devuelven concatenados. Es común utilizar el último Hidden State, es decir, la última salida de la última capa como Input Features para una capa Fully Connected.

A diferencia de otro tipos de Redes como las Convolucionales o FFN, la profundidad en este tipo de redes es de bastante menos impacto.

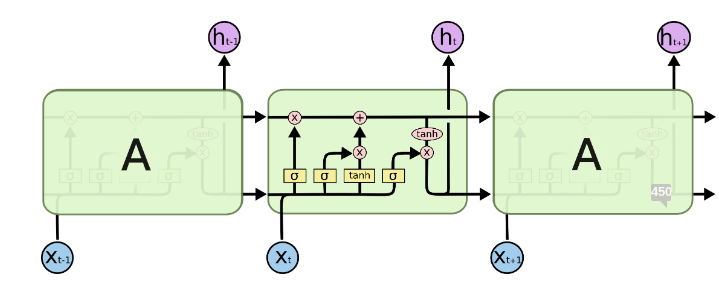
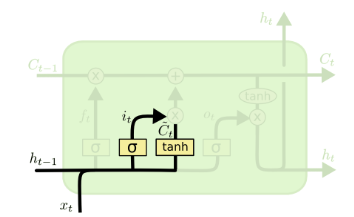
Variantes de RNNs: LSTM (1997)

LSTM (Long Short-Term Memory): Es un tipo de Red Neuronal Recurrente que está diseñada para capturar dependencias de largo plazo abordando algunas de las limitaciones de las RNNs tradicionales, tales como el vanishing gradient problem.

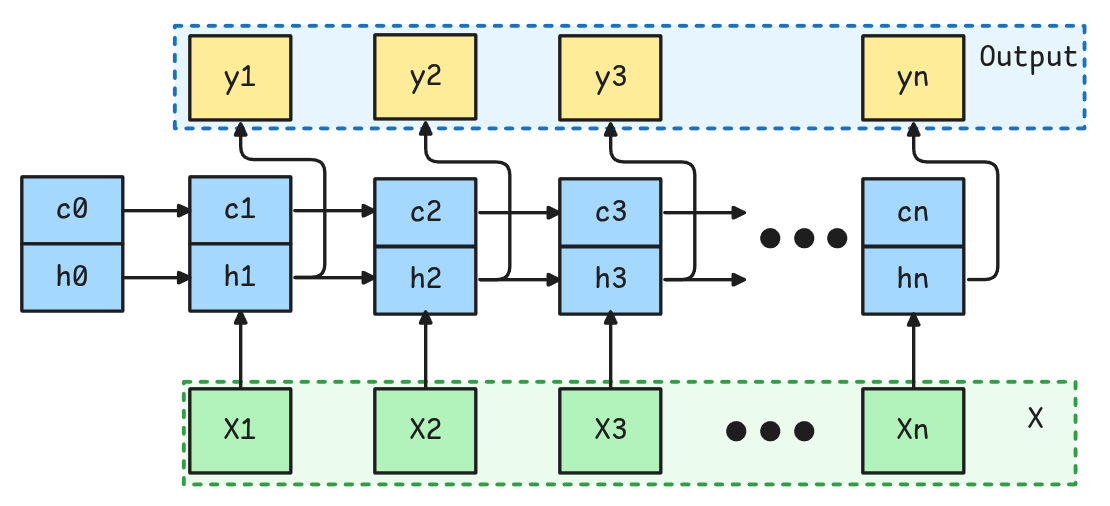
Posee un funcionamiento similar a la RNN, sólo que el “hidden state” se divide en dos partes: $h_t$ y $C_t$, llamados hidden state (corto plazo) y cell state (largo plazo) respectivamente.

Spoiler: El Hidden y Cell State está compuesto por multiples set de parámetros a los cuales se les dan los nombres de forget gate, input gate, cell gate y output gate. Su interpretabilidad nunca ha logrado ser completamente explicada.

Variantes de RNNs: LSTM (1997)

La LSTM está regida por las siguientes ecuaciones:
\[i_t = \sigma(W_{ii}x_t + b_{ii} + W_{hi}h_{t-1} + b_{hi})\]
\[f_t = \sigma(W_{if}x_t + b_{if} + W_{hf}h_{t-1} + b_{hf})\]
\[g_t = tanh(W_{ig}x_t + b_{ig} + W_{hg}h_{t-1} + b_{hg})\]
\[o_t = \sigma(W_{io}x_t + b_{io} + W_{ho}h_{t-1} + b_{ho})\]
\[c_t = f_t \odot c_{t-1} + i_t \odot g_t\]
\[h_t = o_t \odot tanh(c_t)\]

Todas estos elementos $i_t,f_t, g_t,o_t, c_t,h_t \in \mathbb{R}^d$, donde $d$ es el “hidden_size”.

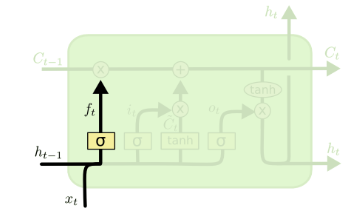
LSTM: Forget Gate

Forget Gate

Corresponde a una red neuronal que indica qué informacion debe ser descartada del Cell State.
Básicamente combina la secuencia en el tiempo t y el hidden state anterior.
Luego se le aplica una Sigmoide que indicará el porcentaje a olvidar.

\[f_t = \sigma(W_{if}x_t + b_{if} + W_{hf}h_{t-1} + b_{hf})\]

LSTM: Input y Cell Gate

Input Gate

Controla Cuánta información debe ingresar al Cell State.

\[i_t = \sigma(W_{ii}x_t + b_{ii} + W_{hi}h_{t-1} + b_{hi})\]

Cell Gate

Representa los potenciales nuevos candidatos a entrar al Cell State.

\[g_t = tanh(W_{ig}x_t + b_{ig} + W_{hg}h_{t-1} + b_{hg})\]

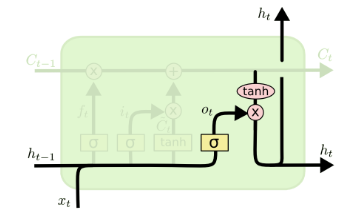
Output Gate y Hidden State

Output Gate

Determina qué “porcentaje” de información del “Cell State” debe salir como “Hidden State” para el tiempo $t$ actual.
\[o_t = \sigma(W_{io}x_t + b_{io} + W_{ho}h_{t-1} + b_{ho})\]

Hidden State

Corresponde a las dependencias del tiempo anterior que se van traspasando en cada time step.
Adicionalmente el Hidden State corresponde a la salida de la red para el tiempo $t$.

\[h_t = o_t \odot tanh(c_t)\]

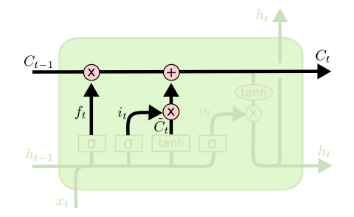
Cell State

Cell State

Representa la principal innovación de este tipo de redes ya que permite recordar dependencias de largo plazo (es decir time steps anteriores en secuencias largas). Esto ya que el Cell State puede avanzar casi sin interacciones lineales (no hay parámetros que influyen en ella, por lo que no es afectada por problemas de gradientes).

\[c_t = f_t \odot c_{t-1} + i_t \odot g_t\]

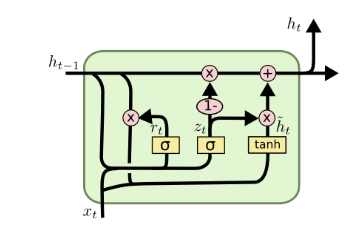
Variantes de RNNs: GRU (2014)

GRU (Gated Recurrent Unit): Corresponde a otro tipo de Arquitectura Recurrente, similar a la LSTM, pero con una estructura más simplificada en la cuál se mantiene sólo un “Hidden State” y se tienen menos gates.

Hidden State

Representa la potencial actualización del “Hidden State”.

\[h_t = (1-z_t) \odot n_t + z_t \odot h_{t-1}\]

Update Gate

Controla qué porcentaje del “hidden state” previo se lleva al siguiente paso.

\[z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz}h_{t-1} + b_{hz})\]

Reset Gate

Controla cuánta información del pasado se debe olvidar.

\[r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr}h_{t-1} + b_{hr})\]

Candidate Hidden State

Representa la potencial actualización del “Hidden State”.

\[n_t = tanh(W_{in} x_t + b_{in} + r_t \odot (W_{hn} h_{t-1} + b_{hn}))\]

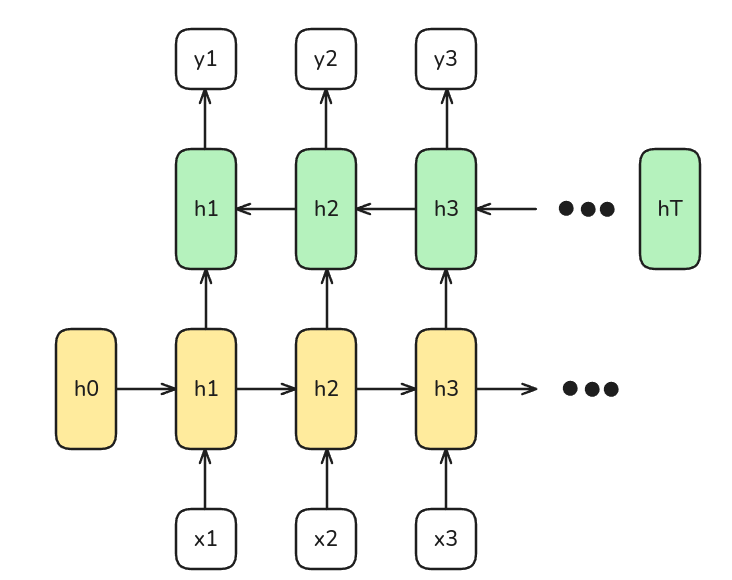
Bidirectional RNNs

Existen ocasiones en las que se requiere no sólo el contexto de los tiempos anteriores, sino también de los posteriores. Por ejemplo, problemas de traducción.

Para ello existen las redes bidireccionales, en la cual se agrega una segunda capa pero que mueve los hidden state en el otro sentido.

En este caso la capa amarilla será la encargada de detectar dependencias del pasado.
Mientras que la capa verde será la encargada de traer dependencias desde el futuro.

Los hidden states pueden ser capas Vanilla RNN, LSTM o GRUs.

Pytorch Layers

nn.RNN(input_size, hidden_size, num_layers=1, batch_first=False, 
        dropout=0, bidirectional=False, nonlinearity="tanh")

nn.LSTM(input_size, hidden_size, num_layers=1, batch_first=False, 
        dropout=0, bidirectional=False)

nn.GRU(input_size, hidden_size, num_layers=1, batch_first=False, 
        dropout=0, bidirectional=False)

input_size: Corresponde al número de features de la secuencia.
hidden_size: Corresponde al número de dimensiones del hidden state.
num_layers: Corresponderá al número de capas recurrentes a apilar, por defecto 1.
batch_first: Este siempre deben fijarlo como True, de esa manera se espera que los tensores a recibir siempre tengan el batch como primera dimensión. Por defecto False.
- Luego RNNs esperan tensores de tamaño $(N,L,H_{in})$. Donde $N$ es el batch_size, $L$ es el largo de secuencia y $H_in$ es el input_size.
dropout: Cantidad de dropout a aplicar a la salida de cada capa, excepto la última. Por defecto 0.
bidirectional: Indica si se hace la red Bidireccional o no. Por defecto False.
nonlinearity: Función de activación a utilizar para activar cada matriz de peso. Puede ser “tanh” o “relu”. Sólo para Vanilla RNN.

TICS-579-Deep Learning

Datos Secuenciales

Time Series (precios de acciones, datos meteorológicos, etc)

Audio (grabaciones de voz, música, etc)

Texto (oraciones, documentos, etc)

Genoma (secuencias de ADN, etc.)

Datos Secuenciales

Image Time Series

Video

¿Cómo se ven datos secuenciales reales?

Redes Neuronales Recurrentes (RNNs)

Recurrent Neural Networks

Implementación Básica de una RNN

Unrolling RNN

Vanishing/Exploding Gradients

Tipos de Tareas a Resolver en Datos Secuenciales

Algunos Ejemplos de Arquitecturas

Stacking RNNs

Variantes de RNNs: LSTM (1997)

Variantes de RNNs: LSTM (1997)

LSTM: Forget Gate

LSTM: Input y Cell Gate

Output Gate y Hidden State

Cell State

Variantes de RNNs: GRU (2014)

Bidirectional RNNs

Pytorch Layers

Eso sería por hoy 😊