TICS-579-Deep Learning
Clase P2: Cálculo Tensorial
Cálculo Tensorial
Derivadas
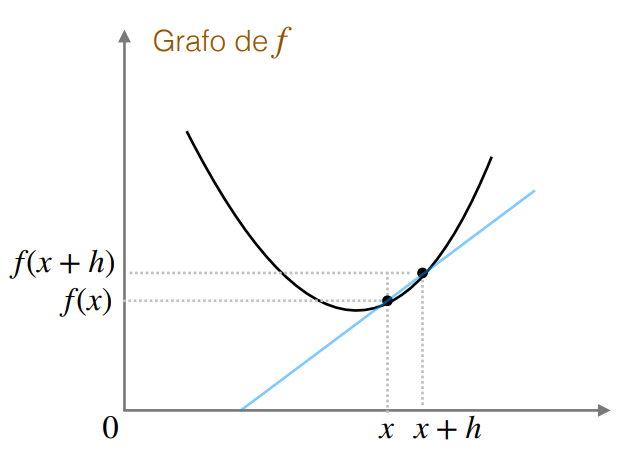
La derivada corresponde a la razón de cambio de una función con respecto a una variable de entrada \(x\). Es decir, cuánto cambia el valor de la función \(f(x)\) cuando cambiamos el valor de \(x\) en una cantidad infinitesimal \(h\).
La definición formal de la derivada
Para una función \(f: \mathbb{R} \rightarrow \mathbb{R}\), la derivada se define como: \[\frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\]
Propiedades
- \(f(x + h) \approx f(x) + f'(x) \cdot h\), cuando \(h \to 0\).
- Si la derivada existe en \(x\), decimos que la función es derivable o diferenciable en \(x\).
- Si las derivadas laterales no existen o no son iguales, entonces \(f\) no es derivable en \(x\).
- Si \(f\) es derivable, entonces \(f\) es continua.
Derivadas: Ejemplos
- \((c)'= 0\)
- \((cx)' = c\)
- \((x^n)' = n x^{n-1}\)
- \((\sqrt{x})' = \frac{1}{2\sqrt{x}}\)
- \((\frac{1}{x})' = -\frac{1}{x^2}\)
- \((e^x)' = e^x\)
- \((ln(x))' = \frac{1}{x}\)
- \((log_a(x))' = \frac{1}{x ln(a)}\)
Reglas de Cálculo
- \((f+g)' = f' + g'\)
- \((fg)' = f'g + fg'\)
- \((\frac{f}{g})' = \frac{f'g - fg'}{g^2}\)
- \((\alpha f)' = \alpha f'\)
- \(f(x) = h(g(x)) \Rightarrow f'(x) = h'(g(x)) g'(x)\), conocida como la regla de la cadena.
Caso Multivariado
Ojo
Si tenemos una función \(f: \mathbb{R}^n \rightarrow \mathbb{R}\). ¿Cómo se define la derivada?
- Se requiere una dirección para derivar. Dado por un vector \(\bar{v} \in \mathbb{R}^n\) y la recta que define.
La definición formal de la derivada direccional
Para una función \(f: \mathbb{R} \rightarrow \mathbb{R}\), la derivada en torno a \(\bar{x}\) en dirección \(\bar{v}\) (\(\bar{v}\) es un vector unitario) se define como: \[\nabla_{\bar{v}}f(x) = \lim_{h \to 0} \frac{f(\bar{x}+h\bar{v}) - f(\bar{x})}{h}\]
Problema
Este cálculo en general es poco práctico debido a que existen infinitas direcciones posibles. Por lo tanto, ¿cuál debería tomar?
Derivadas Parciales
Si \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), se define la derivada parcial de \(f\) en torno a \(\bar{x}=(x_1,...,x_n)\) con respecto a la variable \(x_i\) como como la derivada direccional en la dirección del vector unitario \(\bar{e_i}\).
\[\frac{\partial f(x)}{\partial_{x_i}} = \lim_{h \to 0} \frac{f(x_1, ..., x_i + h, ..., x_n) - f(x_1, ..., x_i, ...x_n)}{h}\]
Gradiente: Función Escalar
Definimos el gradiente de \(f\) como:
\[ \begin{align} \nabla f: \mathbb{R}^n &\rightarrow \mathbb{R}^{1 \times n} \\ \bar{x} &\rightarrow \nabla f(\bar{x}) = \begin{bmatrix}\frac{\partial f}{\partial x_1} & \dots & \frac{\partial f}{\partial x_n}\end{bmatrix} \end{align} \]
El gradiente podríamos considerarlo como un vector fila o columna según conveniencia. Por simplicidad lo dejaremos como un vector fila.
Derivada Direccional en función del Gradiente. ¿Cuál es la dirección en la que la Derivada Direccional es máxima?
\[\nabla_{\bar{v}}f(x) = \nabla f(x) \cdot \bar{v}\]
Gradiente: Ejemplo
\[f(x,y) = 3x^2 + 2xy + y^2 + 5x + 4\]
Consideremos entonces que \(\bar{x} = (x,y)\). Es decir, va de \(\mathbb{R}^2\) a \(\mathbb{R}\).
Gradiente de \(f\)
\[\nabla f(\bar{x}) = \nabla f(x,y) = \begin{bmatrix}\partial f_x & \partial f_y\end{bmatrix} = \begin{bmatrix} 6x + 2y + 5 & 2x + 2y\end{bmatrix}\]
Jacobiano: Función Vectorial
Sea \(f: \mathbb{R}^n \rightarrow \mathbb{R}^k\), el Jacobiano de \(f\) es la generalización del Gradiente y corresponderá a la matriz que contiene las derivadas parciales de una \(f\) multivariada respecto a cada una de sus variables de entrada.
Es decir, si \(f=(f_1(\bar{x}),...,f_k(\bar{x}))^T\)
Entonces,
\[ J = \begin{bmatrix} - \nabla f_1(\bar{x}) -\\ \vdots \\ - \nabla f_k(\bar{x}) -\\ \end{bmatrix} \]
Importante
Podemos pensar el Jacobiano como el “vector de Gradientes” stackeados hacia abajo para cada componente de la función multivariada. Como cada componente es un vector de \(1 \times n\), el Jacobiano tendrá dimensiones \(k \times n\).
Matrices como Transformaciones Lineales
Supongamos:
\[f(x) = A \cdot \bar{x}\]
Caution
- Si \(\bar{x} \in \mathbb{R}^n\) y \(A \in \mathbb{R}^{m \times n}\), entonces \(f(x) \in \mathbb{R}^m\). Es decir, \(f\) es una tranformación que lleva al vector \(\bar{x}\) de \(\mathbb{R}^n\) a un vector de \(\mathbb{R}^m\).
- Entenderemos una Transformación Lineal como una función que toma un vector de entrada (cada componente \(x_j\) es lineal) y lo transforma en otro vector de salida, manteniendo la estructura lineal .
Gradiente de una Transformación Lineal
Si: \[f_i(\bar{x}) = A_{i,:} \cdot \bar{x} = \sum_{j=1}^n A_{i,j}\cdot x_j \implies \frac{\partial f_i}{\partial x_j} = A_{i,j}\]
- \(f_i(\bar{x})\) corresponde a la componente \(i\) de la función vectorial \(f\) evaluada en \(\bar{x}\).
- \(\frac{\partial f_i}{\partial x_j}\) corresponde a la derivada parcial de \(f_i\) respecto a la componente \(x_j\).
- Todas las derivadas se guardan en el Jacobiano de \(f\).
Matrices como Transformaciones Lineales
El Jacobiano de \(f\) es entonces:
\[ J = \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \]
Propiedad
De acá podemos deducir que \(\frac{\partial A \cdot \bar{x}}{\partial \bar{x}} = A\). Es decir el calculo matricial se comporta como las reglas de derivación escalar (al menos lo que usaremos nosotros).
Recomendación
Ver los siguientes videos para entender el concepto de Transformación Lineal de una Matriz:
Hessiano
Hessiano
Si la función a derivar es el Gradiente, entonces el Jacobiano pasa a llamarse Hessiano. Es decir, el Hessiano es el Jacobiano del Gradiente y es equivalente a la segunda derivada de una función vectorial/multivariada.
Propiedades
- El Hessiano es una matriz cuadrada de dimensiones \(n \times n\).
- Siempre es simétrica.
- Si el Hessiano es PSD (Positive Semi-Definite), entonces la función es convexa. Demostrando que \(\bar{x}^T H_f(\bar{x}) \bar{x} \geq 0\) para todo \(\bar{x}\).
\(\nabla f_i(\bar{x})\) corresponde a la componente \(i\) del Gradiente de \(f\) evaluada en \(\bar{x}\).
\[ H_f(\bar{x}) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} = \begin{bmatrix} - \nabla (\nabla f_1(\bar{x})) -\\ - \nabla (\nabla f_2(\bar{x})) -\\ \vdots \\ - \nabla (\nabla f_n(\bar{x})) - \end{bmatrix} \]
Hessiano: Ejemplo
\[f(x,y) = 3x^2 + 2xy + y^2 + 5x + 4\]
Consideremos entonces que \(\bar{x} = (x,y)\). Es decir, va de \(\mathbb{R}^2\) a \(\mathbb{R}\).
Gradiente de \(f\)
\[\nabla f(\bar{x}) = \nabla f(x,y) = \begin{bmatrix}\partial f_x & \partial f_y\end{bmatrix} = \begin{bmatrix} 6x + 2y + 5 & 2x + 2y\end{bmatrix}\]
Hessiano
\[ H_f(\bar{x}) = \begin{bmatrix} - \nabla (\nabla f_1(\bar{x})) - \\ - \nabla (\nabla f_2(\bar{x})) - \\ \end{bmatrix} = \begin{bmatrix} 6 & 2 \\ 2 & 2 \end{bmatrix}\]
Automatic Differentiation
Supongamos que tenemos que calcular la derivada de \(f(1)\) de la siguiente función:
\[f(x) = \sqrt{x^2 + exp(x^2)} + cos((x^2 + exp(x^2))\]
- Su derivada analítica, luego de bastante esfuerzo es:
\[f'(x) = 2x \left(\frac{1}{2\sqrt{x^2+exp(x^2)}} - sen(x^2 + exp(x^2))\right)\left(1+exp(x^2)\right)\] \[f'(1) = 5.983\]
Atención
Calcular la derivada de manera analítica es muy engorroso y propenso a errores. Además, si la función tiene muchas variables, el cálculo se vuelve inviable y difícil de programar. Por ello se utiliza la diferenciación automática, un proceso algorítmico que permite calcular derivadas de funciones complejas de manera eficiente y precisa.
Automatic Differentiation: Ejemplo
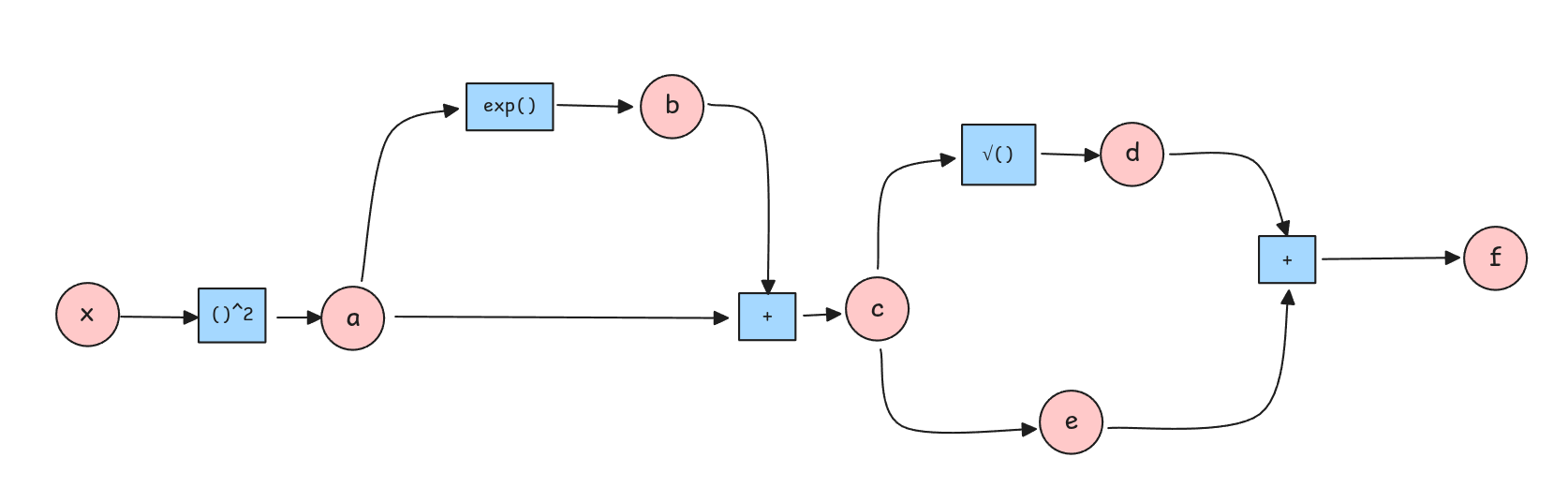
Podemos reescribir la función \(f\) como una secuencia de operaciones elementales y asignar variables intermedias:
Procedimiento
La idea es que el camino entre dos nodos rojos son una derivada entre ambos nodos. Es decir, el camino entre \(f\) y \(d\) es \(\frac{\partial f}{\partial d}\).
Las derivadas se van acumulando y deben considerar todos los caminos. Por ejemplo, para calcular \(\frac{\partial f}{\partial c}\), debemos considerar los caminos \(f \to d \to c\) y \(f \to e \to c\).
Todas las variables definidas permiten calcular sus derivadas respecto a su input.
Si comenzamos a derivar de atrás hacia adelante podemos reutilizar cálculos anteriores.
Automatic Differentiation: Ejemplo
\[\frac{\partial f}{\partial d} = \frac{\partial f}{\partial e} = 1\] \[\frac{\partial f}{\partial c} = \frac{\partial f}{\partial d} \cdot \frac{\partial d}{\partial c} + \frac{\partial f}{\partial e} \cdot \frac{\partial e}{\partial c} = 1 \cdot 0.259 + 1 \cdot 0.545 = 0.8045\] \[ \begin{align} \frac{\partial f}{\partial b} &= \frac{\partial f}{\partial d} \cdot \frac{\partial d}{\partial c} \cdot \frac{\partial c}{\partial b} + \frac{\partial f}{\partial e} \cdot \frac{\partial e}{\partial c} \cdot \frac{\partial c}{\partial b} \\ &= \frac{\partial f}{\partial c} \cdot \frac{\partial c}{\partial b} = 0.8045 \cdot 1 = 0.8045 \end{align} \]
Notar que \(\frac{\partial f}{\partial c}\) ya la habíamos calculado.
\[\frac{\partial f}{\partial a} = \frac{\partial f}{\partial b} \cdot \frac{\partial b}{\partial a} + \frac{\partial f}{\partial c} \cdot \frac{\partial c}{\partial a} = 0.8045 \cdot 2.7183 + 0.8045 \cdot 1 = 2.9913\]
\[\frac{\partial f}{\partial x} = \frac{\partial f}{\partial a} \cdot \frac{\partial a}{\partial x} = 2.9913 \cdot 2 = 5.983\]
Si \(x = 1\), entonces:
\(a = x^2 = 1\)
\(b = exp(a) = 2.7183\)
\(c = a + b = 3.7183\)
\(d = \sqrt{c} = 1.9283\)
\(e = Cos(c) = -0.8383\)
\(f = d + e = 1.09\)
\(\frac{\partial d}{\partial c} = \frac{1}{2\sqrt{c}} = 0.259\)
\(\frac{\partial e}{\partial c} = -sen(c) = 0.545\)
\(\frac{\partial c}{\partial b} = 1\)
\(\frac{\partial b}{\partial a} = exp(a) = 2.7183\)
\(\frac{\partial a}{\partial x} = 2x = 2\)
¿Para qué nos sirve todo esto? 🤔
Método de Newton
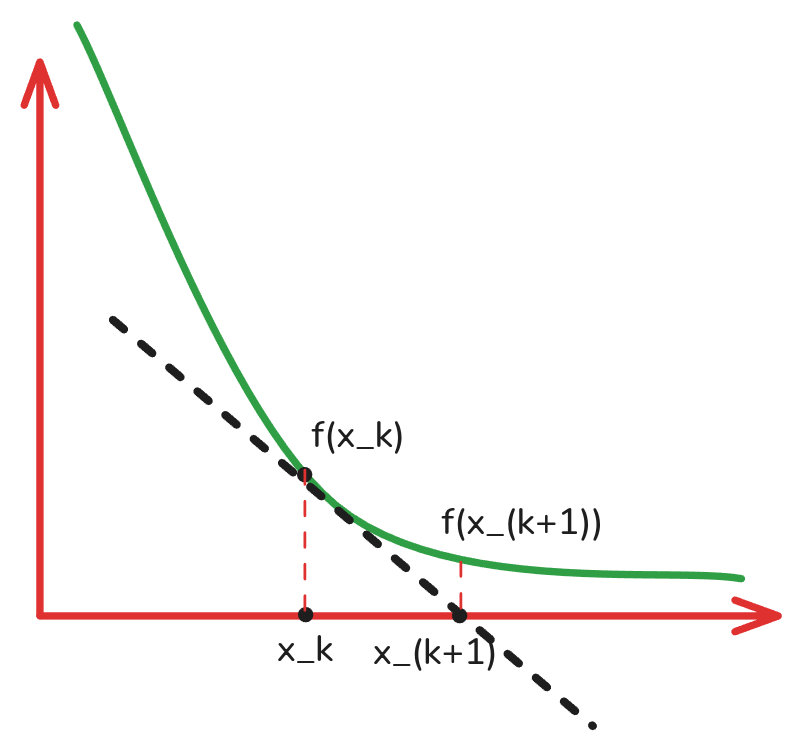
- El método de Newton es un algoritmo iterativo utilizado para encontrar las raíces de una función real (los puntos donde la función se hace cero).
Algotitmo de Newton
- La idea es acercarse de manera iterativa a un punto \(x_{k+1}\) que sea una raíz de la función \(f(x)\) (o al menos se acerque), partiendo de un punto inicial \(x_k\).
- Se asume que me muevo un espacio \(h\).
- Aproximo \(f(x + h)\) utilizando la aproximación local de la función en torno a \(x_k\) como una derivada.
Fórmula de Newton
\[x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}\]
Aplicación como Algoritmo de Optimización
Normalmente cuando necesitamos optimizar una función, buscamos los puntos críticos igualando las derivadas a cero. Es decir:
\[\frac{d f}{d x_i} = 0\]
Si consideramos que \(f\) ahora es una derivada. Entonces el Método de Newton se convierte en un algoritmo de optimización.
\[x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)}\]
Versión Matricial/Multivariada
\[\bar{x_{k+1}} = \bar{x_k} - H_f(\bar{x_k}) \cdot \nabla f(\bar{x_k})\]
Donde \(\nabla f(\bar{x_k})\) es el Gradiente de \(f\) evaluado en \(\bar{x_k}\) y \(H_f(\bar{x_k})\) es el Hessiano de \(f\) evaluado en \(\bar{x_k}\).
Optimización: Gradient Descent
El Algoritmo de Gradient Descent es un método iterativo para encontrar el mínimo de una función. Básicamente es una “simplificación burda” del método de Newton, dado que calcular el Hessiano es costoso y no siempre es necesario.
Para ello se aproxima el Hessiano como una constante \(\alpha\) el cuál llamaremos learning rate. El Gradient Descent queda definido como:
Gradient Descent
\[x_{k+1} = x_k - \alpha \cdot \nabla f(x_k)\]
👀 Ojito
Adicionalmente este método se generalizó no sólo para escalares y/o vectores sino también para matrices y tensores que requieran optimizar cualquier función \(f\).
Otra forma de verlo
Se puede pensar también como que el valor óptimo se encuentra en la dirección opuesta al gradiente moviéndose a un paso constante \(\alpha\).
¡¡Terminamos 😮💨!!