Clasificación de Series de Tiempo en Kaggle.
Reconociendo el Piso usando Redes Neuronales.
Cuando uno comienza a revisar tutoriales de redes neuronales es común encontrarse con los mismos problemas: Regresión o Clasificación Binaria (o en el mejor de los casos problemas multiclase). Pero existen varios otros tipos de problemas que normalmente no se ven y que son sumamente aplicables. En este caso vamos a resolver un problema de Clasificación de Series de Tiempo. Esto significa que le entregaremos a nuestra red una o varias series de tiempo, y la red la nos dirá a qué clase pertenece.
Esto puede ser raro inicialmente, porque estamos acostumbrados a que las series de tiempo llevan registro de un evento en el tiempo y queremos predecir que ocurrirá en el futuro (si te interesa este tema puedes ver un tutorial acá). Pero existen otras aplicaciones de este tipo de problemas, que de hecho pueden ser bien aplicables al tipo de data que estoy trabajando en Jooycar. En este caso lo que haremos es tomar información proveniente de los sensores de un robot para poder predecir en qué tipo de suelo se está moviendo. En el CareerCon 2019 - Help Navigate Robots de Kaggle, se ha recopilado información de sensores de orientación, acelerómetros y velocidad angular de un robot pasando por distintas superficies. Cada una de estas variables es una serie de tiempo. Estas mediciones se han aplicado a 9 tipos distintos de suelo. La tarea es poder utilizar esta información para identificar qué suelo es en el que actualmente se está moviendo el robot.
Esto puede tener muchas aplicaciones prácticas, algunas que se me vienen a la mente (por el rubro en el que estoy trabajando últimamente) son la estimación del estado de las carreteras, predecir las salidas de ruta, entre otros.
Debido a que este problema tiene como objetivo trabajar con data secuencial (las series de tiempo) es que se hace natural el uso de Redes Recurrentes, en particular de las LSTM (Long Short Term Memory). No voy a entrar en detalle de qué son las redes neuronales, pero de nuevo si quieres introducción livianita de que son las LSTMs puedes leer acá.
Partamos entonces con nuestra implementación:
import pandas as pd
import numpy as np
from tqdm.notebook import tqdm
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report, confusion_matrix
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from multiprocessing import cpu_count
from pytorch_lightning.callbacks import ModelCheckpoint, EarlyStopping
import pytorch_lightning as pl
from torchmetrics.functional import accuracy
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import rc
from matplotlib.ticker import MaxNLocator
from pylab import rcParams
pl.__version__
'1.4.2'
pl.seed_everything(42)
Global seed set to 42
X_train = pd.read_csv('career-con-2019/career-con-2019/X_train.csv')
y_train = pd.read_csv('career-con-2019/career-con-2019/y_train.csv')
X_train.head()
| row_id | series_id | measurement_number | orientation_X | orientation_Y | orientation_Z | orientation_W | angular_velocity_X | angular_velocity_Y | angular_velocity_Z | linear_acceleration_X | linear_acceleration_Y | linear_acceleration_Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0_0 | 0 | 0 | -0.75853 | -0.63435 | -0.10488 | -0.10597 | 0.107650 | 0.017561 | 0.000767 | -0.74857 | 2.1030 | -9.7532 |
| 1 | 0_1 | 0 | 1 | -0.75853 | -0.63434 | -0.10490 | -0.10600 | 0.067851 | 0.029939 | 0.003386 | 0.33995 | 1.5064 | -9.4128 |
| 2 | 0_2 | 0 | 2 | -0.75853 | -0.63435 | -0.10492 | -0.10597 | 0.007275 | 0.028934 | -0.005978 | -0.26429 | 1.5922 | -8.7267 |
| 3 | 0_3 | 0 | 3 | -0.75852 | -0.63436 | -0.10495 | -0.10597 | -0.013053 | 0.019448 | -0.008974 | 0.42684 | 1.0993 | -10.0960 |
| 4 | 0_4 | 0 | 4 | -0.75852 | -0.63435 | -0.10495 | -0.10596 | 0.005135 | 0.007652 | 0.005245 | -0.50969 | 1.4689 | -10.4410 |
y_train.head()
Como se puede apreciar existen 12 variables (cada una serie de tiempo) que mide distintos aspectos al momento que el robot se mueve sobre el piso. Es importante destacar que el series_id identifica desde dónde hasta donde es la serie de tiempo. Además permite identificar cuál es la superficie de suelo por el que el robot está circulando.
| series_id | group_id | surface | |
|---|---|---|---|
| 0 | 0 | 13 | fine_concrete |
| 1 | 1 | 31 | concrete |
| 2 | 2 | 20 | concrete |
| 3 | 3 | 31 | concrete |
| 4 | 4 | 22 | soft_tiles |
Explorando
Para poder entender de mejor manera en qué consiste el problema diseñé esta simple función que va a graficar una serie. Toma como único argumento el índice idx y crea un gráfico. Cada uno de los gráficos corresponde en este caso a un tipo distinto de suelo. Como van a ver a continuación algunos generan variaciones más estables, mayor amplitud, más frecuencia, etc. La idea es que la red neuronal pueda entender reconocer el tipo de vibraciones
, mediciones
, sensaciones
captadas por los sensores y pueda dirimir qué tipo de suelo es:
def plot_ts(idx):
return (X_train.query(f'series_id == {idx}').iloc[:,3:]
.plot(figsize = (20,10), title = y_train.iloc[idx]['surface']));
plot_ts(0);
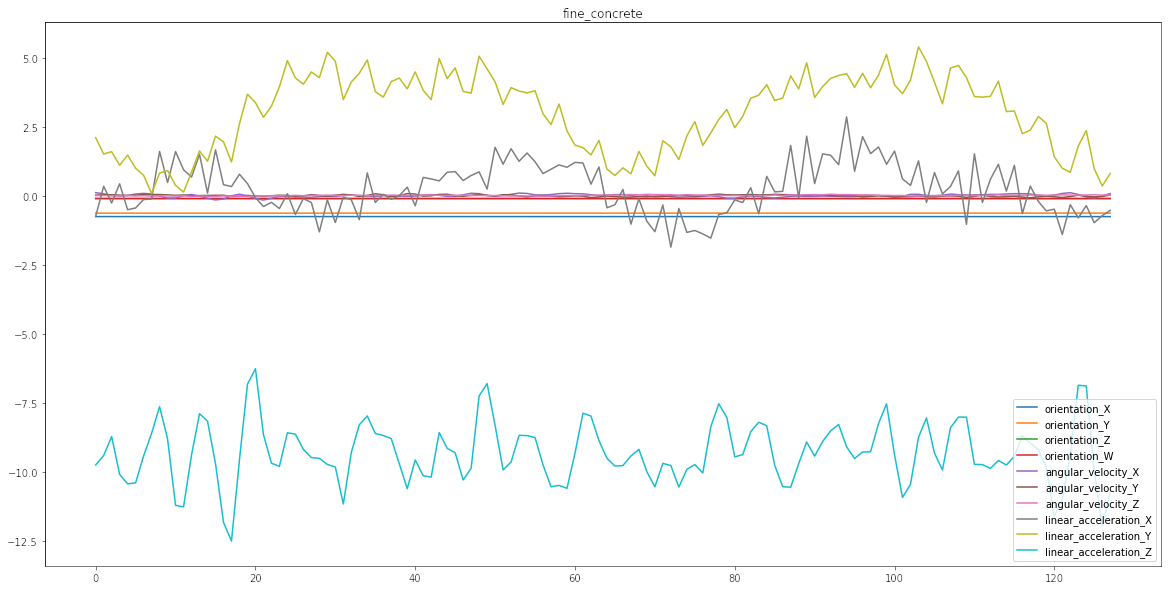
plot_ts(1);
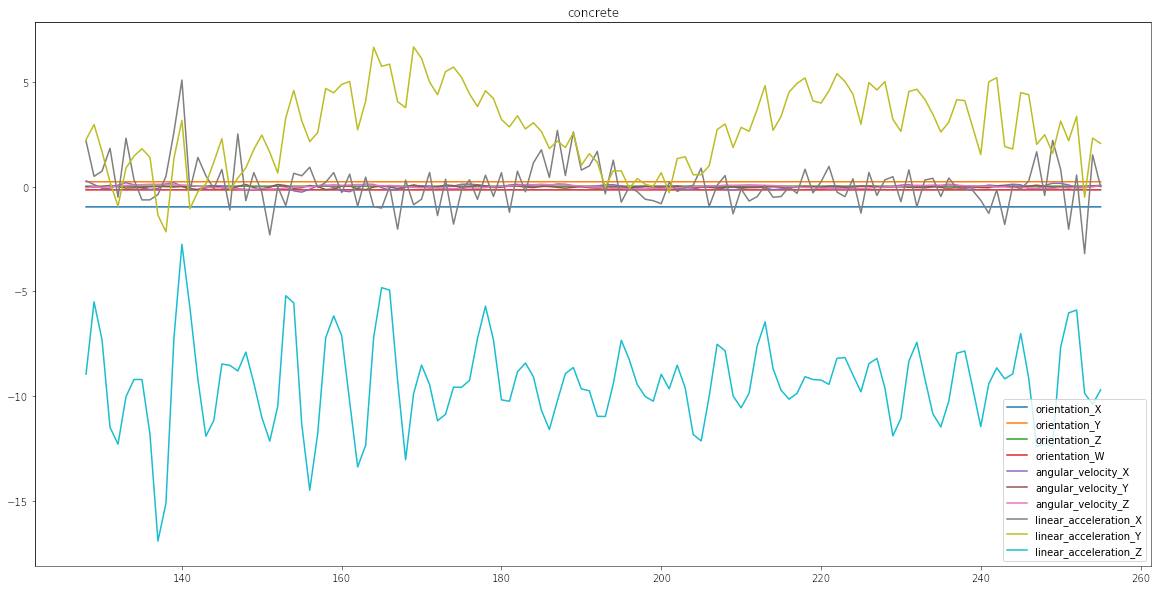
plot_ts(4);
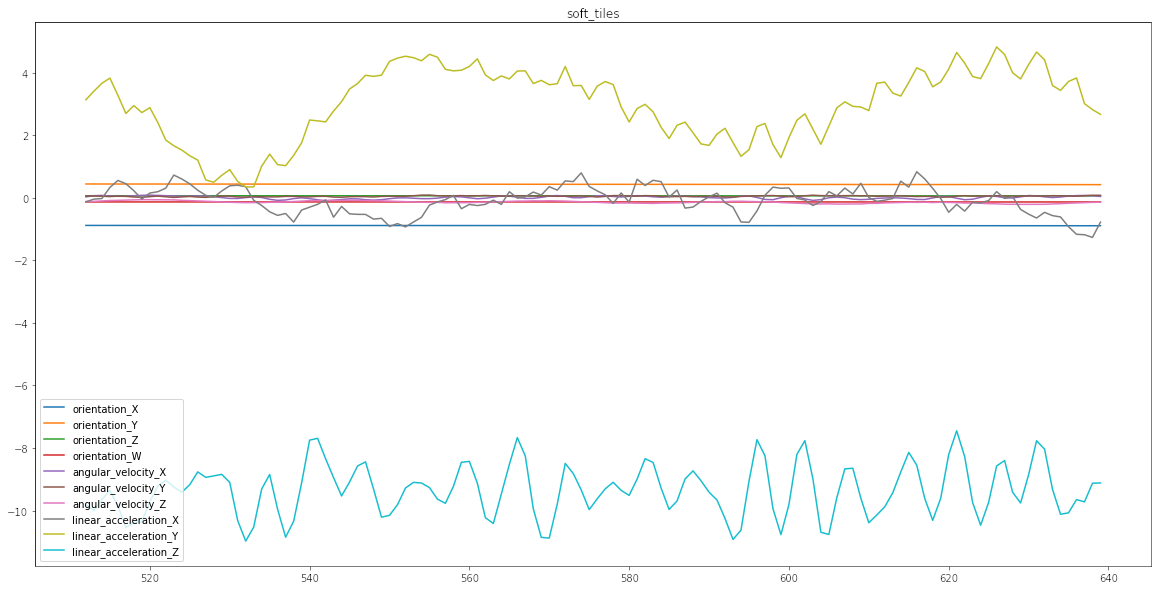
plot_ts(6);
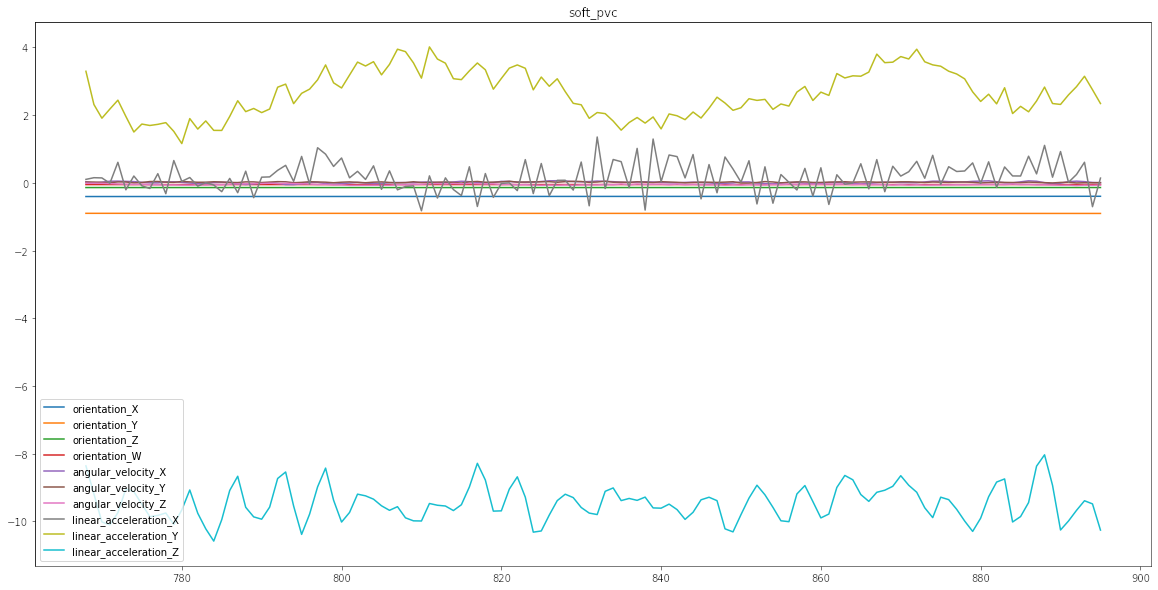
plot_ts(8);
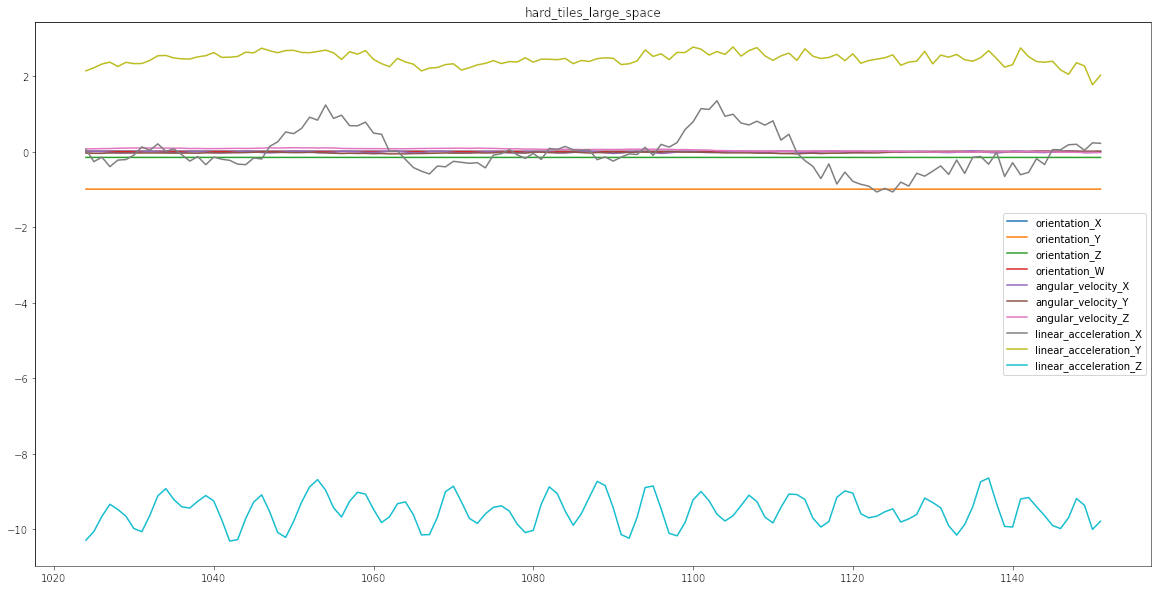
Como se puede apreciar algunos tipos de suelos similares tienen comportamientos similares, lo que es la complejidad asociada al modelo en cuestión.
Preprocesamiento
Utilizaremos el LabelEncoder de Scikit-Learn para poder transformar los distintos tipos de piso en una categoría ordinal:
label_encoder = LabelEncoder()
encoded_labels = label_encoder.fit_transform(y_train.surface)
encoded_labels[:5]
array([2, 1, 1, 1, 6])
La ventaja de utilizar el LabelEncoder es que almacena internamente las clases en el orden asignado:
label_encoder.classes_
array(['carpet', 'concrete', 'fine_concrete', 'hard_tiles',
'hard_tiles_large_space', 'soft_pvc', 'soft_tiles', 'tiled',
'wood'], dtype=object)
y_train['label'] = encoded_labels
y_train.head()
| series_id | group_id | surface | label | |
|---|---|---|---|---|
| 0 | 0 | 13 | fine_concrete | 2 |
| 1 | 1 | 31 | concrete | 1 |
| 2 | 2 | 20 | concrete | 1 |
| 3 | 3 | 31 | concrete | 1 |
| 4 | 4 | 22 | soft_tiles | 6 |
Ahora de todos los campos entregados en el dataset se utilizarán como features predictoras desde la tercera en adelante:
FEATURE_COLUMNS = X_train.columns.tolist()[3:]
FEATURE_COLUMNS
['orientation_X',
'orientation_Y',
'orientation_Z',
'orientation_W',
'angular_velocity_X',
'angular_velocity_Y',
'angular_velocity_Z',
'linear_acceleration_X',
'linear_acceleration_Y',
'linear_acceleration_Z']
Luego es necesario transformar la data en las secuencias correspondientes. A diferencia del problema que resolvimos del Bitcoin donde la data sigue un orden temporal. Acá están asociado a un índice, por lo tanto es necesario separarlas:
sequences = []
for series_id, group in tqdm(X_train.groupby('series_id')):
sequence_features = group[FEATURE_COLUMNS]
label = y_train.query(f'series_id == {series_id}').iloc[0].label
sequences.append((sequence_features, label))
Adicionalmente haremos un split para validar apropiadamente del 20%, obteniendo 3048 secuencias de entrenamiento y 762 de test:
train_sequences, test_sequences = train_test_split(sequences, test_size = 0.2)
len(train_sequences), len(test_sequences)
(3048, 762)
Pytorch Dataset
class SurfaceDataset(Dataset):
def __init__(self, sequences):
self.sequences = sequences
def __len__(self):
return len(self.sequences)
def __getitem__(self, idx):
sequence, label = self.sequences[idx]
return dict(
sequence = torch.tensor(sequence.to_numpy(), dtype = torch.float32),
label = torch.tensor(label).long()
)
En este caso el Pytorch Dataset tomará cada secuencia y la transformará en tensor. Si es que no quieren pasar malos ratos con errores crípticos asegúrense de transformar las secuencias en float32. Por alguna razón las LSTM sólo pueden trabajar con este tipo de datos (aunque creo que pueden trabajar con mixed precision en GPU) en las secuencias. Para el caso de la etiqueta utilizaremos directamente valores enteros (Long en Pytorch).
class SurfaceDataModule(pl.LightningDataModule):
def __init__(self, train_sequences, test_sequences, batch_size):
super().__init__()
self.train_sequences = train_sequences
self.test_sequences = test_sequences
self.batch_size = batch_size
def setup(self, stage = None):
self.train_dataset = SurfaceDataset(self.train_sequences)
self.test_dataset = SurfaceDataset(self.test_sequences)
def train_dataloader(self):
return DataLoader(
self.train_dataset,
batch_size = self.batch_size,
pin_memory = True,
num_workers = cpu_count(),
shuffle = True)
def val_dataloader(self):
return DataLoader(
self.test_dataset,
batch_size = self.batch_size,
pin_memory = True,
num_workers = cpu_count(),
shuffle = False)
def predict_dataloader(self):
return DataLoader(
self.test_dataset,
batch_size = 1,
pin_memory = True,
num_workers = cpu_count(),
shuffle = False)
En el caso del Lightning DataModule crearemos las secuencias y los dataloaders con configuración estándar (pin_memory y todos los núcleos, shuffle sólo en train). El único detalle importante es que para el predict_dataloader utilizo un batch_size de 1, esto para poder manipular los resultados y evaluar el modelo de manera más sencilla.
Spoiler Alert: Evaluaremos el comportamiento utilizando una matriz de confusión. Y para verla más bonita, es mejor hacerlo con Numpy arrays que son tensores.
Pytorch Model
Para resolver este problema utilizaremos un stack de 3 capas de LSTM, las cuales contendrán 256 neuronas en las capas ocultas y están regularizadas con un dropout del 75% (es alto, pero anda bien).
Tomaremos el último hidden state, es decir, la salida de la última capa de LSTMs y la conectaremos a una capa Fully Conected la que finalmente nos dara la clase predicha.
class SequenceModel(nn.Module):
def __init__(self, n_features, n_classes, n_hidden = 256, n_layers = 3):
super().__init__()
self.lstm = nn.LSTM(
input_size = n_features,
hidden_size = n_hidden, # number of neurons for each layer...
num_layers = n_layers,
batch_first = True,
dropout = 0.75
)
self.classifier = nn.Linear(n_hidden, n_classes)
def forward(self, x):
#self.lstm.flatten_parameters() Se necesita en caso de entrenamiento distribuido.
_, (hidden, _) = self.lstm(x)
out = hidden[-1] # Último Hidden State
return self.classifier(out)
Finalmente generamos el Lightning Module con el proceso de entrenamiento.
- Usamos
CrossEntropyLosscomo Loss Function. - Además en el forward aplicamos un truquillo para devolver tanto el loss como el output del batch. Esto sirve para evitar un loop adicional para extraer esta info.
- Dado que se trata de un problema multiclase, la predicción final se obtiene con un argmax a la última capa de la Capa Fully Connected.
Para quienes vienen de Tensorflow puede que les extrañé que no estamos utilizando una función Softmax como activación de la capa de salida. Los que han estudiado en más profundidad las redes neuronales en problemas multiclase, sabrán que la Softmax sufre de un problema de Overflow. Por lo tanto, en Pytorch para evitar ese tipo de inconvenientes la SoftMax está incluida al interior de la CrossEntropyLoss, por lo tanto no es necesaria aplicarla. Ahora la Función Softmax tiene como único propósito normalizar el output de cada neurona de salida en el intervalo 0 a 1. Por lo que si se aplica un argmax a la salida se obtendrá el mismo resultado aplicando o no esta función de activación.
class SurfacePredictor(pl.LightningModule):
def __init__(self, n_features: int, n_classes: int):
super().__init__()
self.model = SequenceModel(n_features, n_classes)
self.criterion = nn.CrossEntropyLoss()
def forward(self, x, labels = None):
output = self.model(x)
loss = 0
if labels is not None:
loss = self.criterion(output, labels)
return loss, output
def training_step(self, batch, batch_idx):
sequences = batch['sequence']
labels = batch['label']
loss, outputs = self(sequences, labels)
predictions = torch.argmax(outputs, dim = 1)
step_accuracy = accuracy(predictions, labels)
self.log('train_loss', loss, prog_bar = True, logger = True)
self.log('train_accuracy', step_accuracy, prog_bar = True, logger = False)
return {'loss': loss, 'accuracy': step_accuracy}
def validation_step(self, batch, batch_idx):
sequences = batch['sequence']
labels = batch['label']
loss, outputs = self(sequences, labels)
predictions = torch.argmax(outputs, dim = 1)
step_accuracy = accuracy(predictions, labels)
self.log('val_loss', loss, prog_bar = True, logger = True)
self.log('val_accuracy', step_accuracy, prog_bar = True, logger = False)
return {'loss': loss, 'accuracy': step_accuracy}
def predict_step(self, batch, batch_idx, dataloader_idx=None): # dataloader_idx: not needed
sequences = batch['sequence']
labels = batch['label']
loss, outputs = self(sequences, labels)
predictions = torch.argmax(outputs, dim = 1)
return labels, predictions
def configure_optimizers(self):
return torch.optim.Adam(self.parameters(), lr = 0.0001)
Acá tengo un detalle que destacar. Y es que en la versión actual de Pytorch Lightning que es la 1.4.2 hubo un cambio en el predict_step y es que ahora se debe colocar dataloader_idx = None. Este cambió fue muy under. De hecho, para el problema de Bitcoin se me olvidó agregar el parámetro dataloader_idx por lo cual no me arrojó ningún error. Y si bien parece ser que es un parámetro sin uso definido, la documentación recomienda agregarlo así. Probablemente haré un update en el post de Pytorch Lightning.
Entrenamiento
Para entrenar esta red neuronal se decidió utilizar un batch_size de 64 durante 250 Epochs. Intenté entrenar esto en mi Laptop a modo de prueba y fue eterno. Así que nuevamente utilicé JARVIS el cual se demoró la módica suma de 11 minutos en entrenar en GPU.
Adicionalmente utilizaremos un model Checkpoint para ir guardando los pesos en las epochs con el mejor val_loss (el mínimo).
N_EPOCHS = 250
BATCH_SIZE = 64
data_module = SurfaceDataModule(train_sequences, test_sequences, BATCH_SIZE)
model = SurfacePredictor(n_features=len(FEATURE_COLUMNS), n_classes = len(label_encoder.classes_))
checkpoint_callback = ModelCheckpoint(
dirpath = 'checkpoints',
filename = 'best-checkpoint',
save_top_k = 1,
verbose = True,
monitor = 'val_loss',
mode = 'min'
)
trainer = pl.Trainer(callbacks = [checkpoint_callback],
max_epochs = N_EPOCHS,
gpus = 1,
progress_bar_refresh_rate = 30,
deterministic=True,
fast_dev_run=False)
/home/alfonso/miniconda3/envs/kaggle/lib/python3.7/site-packages/pytorch_lightning/callbacks/model_checkpoint.py:446: UserWarning: Checkpoint directory checkpoints exists and is not empty.
rank_zero_warn(f"Checkpoint directory {dirpath} exists and is not empty.")
GPU available: True, used: True
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
trainer.fit(model, data_module)
Evaluación del Modelo
Asumiendo que el modelo se ha entrenado y que se está cargando en un kernel limpio, distinto al de entrenamiento, es que se puede utilizar load_from_checkpoint para rescatar el mejor Checkpoint (como en los juegos).
trained_model = SurfacePredictor.load_from_checkpoint(
"checkpoints/best-checkpoint-v1.ckpt",
n_features = len(FEATURE_COLUMNS),
n_classes = len(label_encoder.classes_)
)
Además, todavía no estoy 100% seguro de por qué aplicar el freeze. Se supone que esto se aplica para impedir que hayan cambios en los pesos del modelo por la acumulación de gradientes, pero sigo buscando una buena explicación al respecto.
trained_model.freeze()
trained_model
SurfacePredictor(
(model): SequenceModel(
(lstm): LSTM(10, 256, num_layers=3, batch_first=True, dropout=0.75)
(classifier): Linear(in_features=256, out_features=9, bias=True)
)
(criterion): CrossEntropyLoss()
)
Finalmente para predecir es necesario correr el setup() del datamodule y aplicar el predict en el trainer.
data_module.setup()
preds = trainer.predict(model = trained_model, datamodule = data_module)
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
Predicting: 0it [00:00, ?it/s]
Se está asumiendo que esta predicción se hace en un kernel distinto al que se utilizó para poder entrenar el modelo. Por lo tanto no existe evidencia en memoria del dm.setup(), es decir, la data no está con el formato adecuado para el modelo hasta la ejecución de este método.
trainer.validate(model = trained_model)
/home/alfonso/miniconda3/envs/kaggle/lib/python3.7/site-packages/pytorch_lightning/core/datamodule.py:424: LightningDeprecationWarning: DataModule.prepare_data has already been called, so it will not be called again. In v1.6 this behavior will change to always call DataModule.prepare_data.
f"DataModule.{name} has already been called, so it will not be called again. "
/home/alfonso/miniconda3/envs/kaggle/lib/python3.7/site-packages/pytorch_lightning/core/datamodule.py:424: LightningDeprecationWarning: DataModule.setup has already been called, so it will not be called again. In v1.6 this behavior will change to always call DataModule.setup.
f"DataModule.{name} has already been called, so it will not be called again. "
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
Adicionalmente descubrí que el .validate() o el .test() sólo están disponibles luego de un .fit() o de un .predict(). De acuerdo a la nomenclatura de Scikit-Learn deberían tener un _ de sufijo para evitar malos ratos. El mal rato es más que nada porque no falla, sino que entrega un resultado vacío. Al parecer es un bug en el cual ya se está trabajando (por eso el warning de arriba) y pronto debería solucionarse para que siempre que se aplique un método del Trainer haya un .setup() invisible.
--------------------------------------------------------------------------------
DATALOADER:0 VALIDATE RESULTS
{'val_accuracy': 0.8123359680175781, 'val_loss': 0.5650554299354553}
--------------------------------------------------------------------------------
Como se puede ver el modelo estuvo espectacular, se logró alrededor de un 81% de Accuracy que es la métrica utilizada en el entrenamiento.
Análisis de los Resultados
Para analizar los resultados de mejor manera se utilizará una matriz de confusión (sólo que un poquito más bonita, porque es la versión de Scikit-Plot).
labels = torch.tensor(preds)[:,0].numpy()
predictions = torch.tensor(preds)[:,1].numpy()
from scikitplot.metrics import plot_confusion_matrix
ax = plot_confusion_matrix(labels, predictions, figsize = (10,8))
ax.set_xticklabels(label_encoder.classes_, rotation = 90, fontsize = 10)
ax.set_yticklabels(label_encoder.classes_, fontsize = 10);
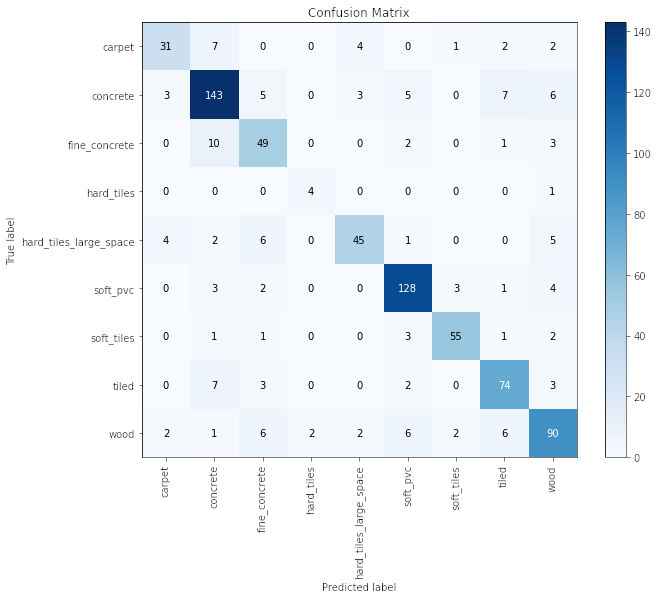
Algunos de los insights que se pueden obtener son:
- Parece ser que los que más éxito tuvieron fueron los de
ConcreteySoft PVC. - Donde se ven más confusiones viene a ser el
Wood. Probablemente dependiendo del tipo de madera podría haber más o menos vibraciones que lo llevan a ser un piso propenso a Falsos Positivos. - Los
Hard Tilesfueron super éxito. Eran muy poquitos pero se pudieron predecir 4/5 de manera correcta. - Un error importante (aunque entendible) es que la mayor cantidad de confusiones se dan entre
ConcreteyFine Concrete,TiledyCarpet.
Aún siendo que hay confusiones/errores por parte del modelo, y de que la métrica ronda el 80% se puede ver que es un modelo sumamente aplicable y funcional.
Bueno,
Espero que haya sido interesante salirse de lo más común para resolver otro problema de Kaggle como este. Debo reconocer que me sacó hartas canas este problema porque hubo harto error críptico que decifrar, pero aprendí mucho y siento que cada vez me siento más cómodo utilizando Pytorch y Pytorch Lightning.
Nos vemos para la otra!!
