En un país donde las ofertas de puestos de Data Scientist aparecen por todas partes es muy importante estar preparado. Me llama especialmente la atención que hay muy pocas entrevistas técnicas que evalúan el conocimiento de los Data Scientist a contratar. Esto puede ser útil si eres nuevo, porque puede ser más sencillo entrar el mundillo este. Pero eventualmente, debemos llegar a estándares más altos donde se cuestionarán las habilidades que uno tiene. Siempre se cuentan los casos de éxitos, pero yo quiero contar mi máximo FAIL.

Estaba postulando a una empresa súper prestigiosa en términos de Machine Learning, y la verdad es que iba bien preparado a la entrevista. Había pasado una prueba bien dura de programación, y me tocaba una entrevista de teoría. Siendo honesto, no estudié tanto, porque ya estaba full haciendo clases y consideraba que tenía buena preparación teórica. Y bueno, pensé que lo más complejo que me podían preguntar era qué es el p-value (que creo que no sé como explicar).

Llegué a la entrevista, eran 10 preguntas, yo sentí que estaba contestando bien, hasta que en la pregunta 9 me dice vamos a hablar de algoritmos no supervisados. Y me entró el escalofrío. Se usa poco en la práctica (al menos bastante menos que los algoritmos supervisados). Con suerte se usa para hacer segmentaciones. Y la verdad no lo tengo para nada en memoria. Me hace la primera pregunta: ¿Qué precauciones debemos tener antes de usar K-Means? Siento que la respondí bastante bien, me había tocado hacer segmentaciones por lo que tenía super claro como preprocesar la data y en qué fijarme al momento de utilizarlo. Pregunta 10: Explícame en detalle, cada paso del algoritmo de K-Means. 😱 En ese momento me dí cuenta de que me faltó estudiar. Tenía una idea en la cabeza porque había implementado un K-means desde cero en Python puro cuando dí el XCS229 del Programa de Inteligencia Articial que tomé en Stanford (el cual recomiendo totalmente si es que les interesa la parte teórica del ML), pero no me podía acordar cómo se actualizaba el centro de cada cluster. Expliqué todo lo que sabía, evitando (más bien saltándome) lo que no recordaba. Entonces, el entrevistador me dijo: Oye, está super bien, pero no me queda claro cómo se actualizan los centros de cada cluster: 😨 Me pilló. En las reglas de la entrevista decía que si uno no sabía algo podía decir que no sabía, así que le dije: Pucha, no recuerdo esa parte.. No me llamaron más (así que asumí que no quedé 😇).

Si bien este tipo de entrevistas no son tan comunes, cuando quieres postular a empresas que se dedican a hacer Machine Learning en serio (y no sólo a hacer los típicos modelos de Propensión, Churn, Segmentaciones, etc.) hay que entender el proceso a fondo. Y en este caso el no recordar que los centroides se actualizan promediando los puntos del clúster (por eso K-Means) me costó no quedar en el puesto (lo cual todavía lamento).

El algoritmo de K-Means

La verdad es que este algoritmo es bien sencillito. Básicamente tienes puntos en un espacio y quieres armar comunidades (clústers) de puntos que se parezcan, es decir que sean cercanos. Para ello se siguen los siguientes pasos:

• Se decide el número de Clusters. K-Means no es capaz de decidir a priori cuántos clusters utilizar. Por lo tanto , éstos se tienen que dar de antemano (es decir, es un hiperparámetro). Las coordenadas para cada centroide del cluster se inicializarán de manera aleatoria.
• Cada punto es asignado a un Cluster. Para esto se define cuál es la distancia de cada punto a cada centroide y se asignará al cluster que tenga la menor distancia a su centroide.
• Se actualizan los centroides (mi fail). Se toman todos los puntos pertenecientes a un cluster y se promedian, este resultado corresponderá a las coordenadas del nuevo centroide.
• Se repiten los pasos 2 y 3 hasta lograr la convergencia. La convergencia se logra cuando ya no hay variación de los centroides entre cada iteración.

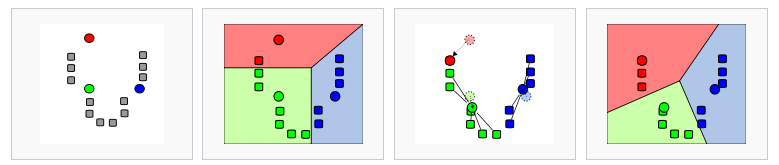
En fin, no es necesario aplicar este algoritmo “from scratch”, ya que de hecho este es un problema de complejidad NP-Hard (baśicamente, díficil de optimizar) y Scikit-Learn tiene una implementación muy óptimizada y fácil de usar.

Ahora la aplicación que quiero mostrar es una bien interesante de “Image Compression”. Básicamente bajar la calidad de la imágen. Para ello haremos lo siguiente:

from sklearn.cluster import KMeans
from matplotlib.image import imread
import pandas as pd
import matplotlib.pyplot as plt

full_resolution_img = imread('peppers-large.tiff')
plt.figure(figsize = (10,10))
plt.imshow(full_resolution_img)
plt.axis('off');

Si les interesa replicar el procedimiento pueden descargar la imágen acá.

full_resolution_img.shape

(512, 512, 3)

Como se puede ver, se trata de una imagen de 3 canales (RGB) de resolución 512x512 pixeles. Qué pasaría, si en vez de tratar la imagen en este formato la cambiamos de la siguiente manera:

pixels = full_resolution_img.reshape(-1,3)/255
pixels.shape

(262144, 3)

En este caso obtenemos una lista de cada uno de los pixeles. Podríamos decir entonces que luego del reshape tenemos un dataset con todos los colores (combinaciones de Rojo, Verde y Azul) utilizados en la imagen.

Acá es donde entra el K-Means. Podemos de cierta manera generar clusters, que pueden ser interpretados como agrupaciones de colores. Esto resultará en modificar nuestra imagen original de 24 bits a una versión más comprimida.

Para hacer la compresión haremos entonces 16 clusters. Esto nos dará 4 bits por canal, por lo tanto tendríamos imágenes de 12 bits.

kmeans = KMeans(n_clusters=16, random_state=123)
cluster = kmeans.fit_predict(pixels)
cluster

array([ 6, 14, 14, ...,  5,  2,  2], dtype=int32)

pd.Series(cluster).value_counts()

13    30027
7     30020
1     25541
10    24267
4     22099
11    19800
15    16150
3     15094
0     14131
12    13174
6     12862
5     11570
2     10958
8     10471
9      5475
14      505
dtype: int64

Como se puede apreciar, ahora sólo tenemos 16 clusters. Estos 16 clusters podrían representar 16 colores principales, que por la definición del K-Means serán el promedio de los colores del cluster. Como sólo pueden haber 16 valores distintos por cada canal, eso es 2⁴, luego, tenemos 4 bits. Ahora, no nos interesa el identificador del cluster que es el resultado del .fit_predict(), más bien, nos interesan los centroides de cada cluster, ya que como bien dijimos, estos representarán un color promedio. Para obtener esto en Scikit-Learn hacemos lo siguiente:

centers = kmeans.cluster_centers_
centers

array([[4.59789396e-01, 4.15149528e-01, 2.04456932e-01],
       [7.22265979e-01, 1.58838576e-01, 1.48959576e-01],
       [7.58603080e-01, 8.57161927e-01, 7.55448074e-01],
       [1.82948346e-01, 6.77831811e-03, 4.25771793e-03],
       [6.08454512e-01, 7.00841351e-01, 3.05950520e-01],
       [7.19107297e-01, 7.99673203e-01, 5.67397973e-01],
       [3.45444096e-01, 4.45862526e-02, 4.21471318e-02],
       [7.25751102e-01, 7.89391203e-01, 3.47212740e-01],
       [4.43207003e-01, 2.40346951e-01, 1.42962325e-01],
       [7.92388091e-01, 4.49669623e-01, 2.95399065e-01],
       [4.73568103e-01, 6.75029949e-01, 3.31192368e-01],
       [4.47121988e-01, 5.61503086e-01, 2.56008633e-01],
       [5.50247767e-01, 7.49612934e-01, 4.39358419e-01],
       [7.97094883e-01, 2.23587943e-01, 1.71642967e-01],
       [5.96233741e-01, 1.49880108e-15, 7.21871481e-01],
       [5.70648315e-01, 8.48032237e-02, 9.75248360e-02]])

Finalmente, lo que nosotros queremos es que cada color original sea reemplazado con las coordenadas del centroide de su cluster. Esto se puede lograr de manera muy sencilla tan solo incluyendo los clusters dentro del dataset de centros. Esto puede ser raro al inicio, y es más bien un truco matricial. La mejor manera de pensarlo es como que el id del cluster es el índice de cada centroide, y voy a llamar a dichas coordenadas en el orden en el que resultó mi clustering (output del fit_predict()).

Finalmente para reconstruir la imagen tengo que volverlo a la forma original de 512x512 y listo!!

new_image = centers[cluster].reshape(512,512,3)
plt.figure(figsize = (10,10))
plt.imshow(new_image)
plt.axis('off');

fig, ax = plt.subplots(1,2, figsize = (20,20))
ax[0].imshow(full_resolution_img)
ax[0].axis('off')
ax[1].imshow(new_image)
ax[1].axis('off')

Espero, que con esto no se me olvide nunca más el funcionamiento del algoritmo de K-means. Y tambien espero que les haya parecido interesante.

Nos vemos a la otra,

Alfonso