Detección de Anomalías en Series de Tiempo
Implementando DeepAnt
Bueno, como les comenté en los post anteriores, mi tema de investigación está siendo el uso de Anomalías en Series de Tiempo utilizando Deep Learning. Por lo que comencé por implementar mi primer Paper y publicándolo en Papers with Code por lo que les agradecería encarecidamente que si aprendieron algo nuevo me dieran una estrellita en el Github para que gane popularidad.
Además, creo que gran parte del valor de un tutorial es que puedan reproducirlo, por lo que de ahora en adelante podrán reproducirlo sin casi nada de configuración en Google Colab. Sólo clickeen en Open in Colab e instalen las dependencias. Perdón que el Notebook esté en Inglés pero lo estoy usando como parte de la publicación en Papers with Code. Prometo que otros estarán en español.
El código completo lo encontrarán en el Notebook, por lo que sólo incluiré el código más interesante a explicar.
DeepAnt
Bueno DeepAnt es un algoritmo de Detección de Anomalías en series de tiempo. Su principal usi es detectar comportamiento anormal de una medición en el tiempo de manera no supervisada, es decir, no tenemos etiquetas para validar qué partes de las series de tiempo son anómalas o no. Esto es particularmente importante debido a que las anomalías son raras, no tenemos cómo saber a priori cómo son y cómo se ven. Algunas de las principales aplicaciones de la Detección de Anomalías son Detección de Fraude, comportamientos inusuales, etc.
En este caso lo que haremos es reproducir el algoritmo en uno de los dataset de prueba utilizados en el paper. Este dataset chequea el tiempo de demora en tráfico en Minnesota, y la tarea es detectar cuáles de esos tiempos son son correctos.
Para ello DeepAnt propone una arquitectura utilizando Redes Convolucionales de 1 dimensión para análisis de secuencias. Lo más común para resolver este tipo de problemas es utilizar redes recurrentes pero en este caso, las redes convolucionales funcionan bastante bien.

Obviamente lo común es pensar que las Redes Convolucionales se utilizan sólo en Imágenes, pero una Red Convolucional de 1D es como una imagen pero sin alto, solo con ancho.
Investigando y adentrándome más en el tema se definen 3 tipos de algoritmos para la detección de Anomalías: Forecast Based, Reconstruction Based y mixtos. DeepAnt es ForecastBased, lo que quiere decir que va a intentar predecir uno más a puntos con la hipótesis que valores anómalos serán más dificiles de predecir. Luego las predicciones pasarán por una métrica de error, este caso Norma L2, Los puntos con más error serán considerados anomalías.
Si quieres conocer cómo funciona uno Reconstruction Based, puedes ir acá.
La métrica L2 se define como: \[L2 = ||y_{pred}-y||_2 = \sqrt{(y_{pred}-y)^2}\]
Data
Al revisar nuestra data nos encontramos con esto:
df = pd.read_csv('data/TravelTime_451.csv', index_col = 'timestamp', parse_dates=['timestamp'])
df.plot(figsize = (15, 6), title = 'Travel Time', legend = False);
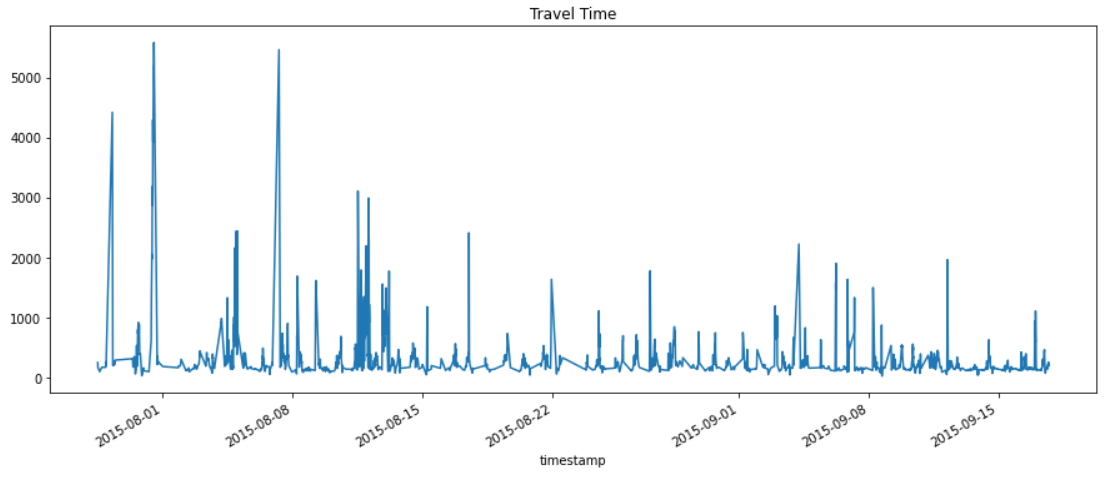
Se puede ver claramente que la data tiene unos peaks que podrían ser eventualmente inusuales.
Para el entrenamiento del modelo el Paper propone crear minisecuencias, supongamos que tenemos una series de Tiempo TS de 5 Puntos: \[TS = \{x_1, x_2, x_3, x_4, x_5\}\]
Por ejemplo, las secuencias $S_i$ de largo 2 serían así: \[S_i = \{x_{i-2}, x_{i-1}\} \rightarrow x_i\]
Es decir, el punto $x_i$ se trataría de predecir con los dos puntos inmediatamente anteriores.
Esto podemos implementarlo en Pytorch de la siguiente manera:
class TrafficDataset(Dataset):
def __init__(self, df, seq_len):
self.df = df
self.seq_len = seq_len
self.sequence, self.labels, self.timestamp = self.create_sequence(df, seq_len)
def create_sequence(self, df, seq_len):
sc = MinMaxScaler()
index = df.index.to_numpy()
ts = sc.fit_transform(df.value.to_numpy().reshape(-1, 1))
sequence = []
label = []
timestamp = []
for i in range(len(ts) - seq_len):
sequence.append(ts[i:i+seq_len])
label.append(ts[i+seq_len])
timestamp.append(index[i+seq_len])
return np.array(sequence), np.array(label), np.array(timestamp)
def __len__(self):
return len(self.df) - self.seq_len
def __getitem__(self, idx):
return (torch.tensor(self.sequence[idx], dtype = torch.float).permute(1, 0),
torch.tensor(self.labels[idx], dtype = torch.float))
El método create_sequence() creará la secuencia escalada en el rango [0.1]. Hacer este preprocesamiento genera más estabilidad en el entrenamiento. Además se crea la etiqueta a utilizar dependiendo del SEQ_LEN dado. Además guardaremos el timestamp asociado a la etiqueta para poder identificar dónde ocurren las anomalías. El resto corresponde a la estructura de Pytorch Dataset para incluirlo posteriormente en los DataLoaders.
Luego, viene el DataModule. Este permitirá indicar el proceso de entrenamiento:
class DataModule(pl.LightningDataModule):
def __init__(self, df, seq_len):
super().__init__()
self.df = df
self.seq_len = seq_len
def setup(self, stage=None):
self.dataset = TrafficDataset(self.df, self.seq_len)
def train_dataloader(self):
return DataLoader(self.dataset, batch_size = 32, num_workers = 10, pin_memory = True, shuffle = True)
def predict_dataloader(self):
return DataLoader(self.dataset, batch_size = 1, num_workers = 10, pin_memory = True, shuffle = False)
En este caso sólo tenemos dos DataLoaders idénticos excepto por el batch size: 32 para entrenar con shuffle, y 1 para predecir. Sólo por un tema de organizar las predicciones de manera más fácil (y sin shuffle).
Luego la Arquitectura de DeepAnt:
class DeepAnt(nn.Module):
def __init__(self, seq_len, p_w):
super().__init__()
self.convblock1 = nn.Sequential(
nn.Conv1d(in_channels=1, out_channels=32, kernel_size=3, padding='valid'),
nn.ReLU(inplace=True),
nn.MaxPool1d(kernel_size=2)
)
self.convblock2 = nn.Sequential(
nn.Conv1d(in_channels=32, out_channels=32, kernel_size=3, padding='valid'),
nn.ReLU(inplace=True),
nn.MaxPool1d(kernel_size=2)
)
self.flatten = nn.Flatten()
self.denseblock = nn.Sequential(
nn.Linear(32, 40),
#nn.Linear(96, 40), # for SEQL_LEN = 20
nn.ReLU(inplace=True),
nn.Dropout(p=0.25),
)
self.out = nn.Linear(40, p_w)
def forward(self, x):
x = self.convblock1(x)
x = self.convblock2(x)
x = self.flatten(x)
x = self.denseblock(x)
x = self.out(x)
return x
Como se puede ver se compone de 3 Bloques + la salida:
- 2 Bloques Convolucionales de 32 Filtros con una Capa Convolucional 1D Relu y MaxPool1D. El Kernel Convolucional es 3x3, mientras que el Pooling es 2x2.
- Una capa flatten para conectar con la Capa Densa.
- Una capa Hidden de 40 Neuronas más Relu y Dropout de 25%.
- Finalmente la capa de Predicción con salida p_w. El paper indica que de predecir anomalías puntuales se usa p_w = 1, que es el caso implementado. En caso de predecir secuencias se puede usar p_w, con el correspondiente ajuste a la creación de secuencias.
Finalmente el LightningModule:
class AnomalyDetector(pl.LightningModule):
def __init__(self, model):
super().__init__()
self.model = model
self.criterion = nn.L1Loss()
def forward(self, x):
return self.model(x)
def training_step(self, batch, batch_idx):
x, y = batch
y_pred = self(x)
loss = self.criterion(y_pred, y)
self.log('train_loss', loss, prog_bar=True, logger = True)
return loss
def predict_step(self, batch, batch_idx):
x, y = batch
y_pred = self(x)
return y_pred, torch.linalg.norm(y_pred-y)
def configure_optimizers(self):
return torch.optim.Adam(self.parameters(), lr = 1e-5)
De acuerdo al Paper se entrena el modelo con MAE Loss (L1Loss en Pytorch) durante 30 epochs. Para la predicción, no nos interesa la predicción propiamente tal, sino que la Norma L2 (torch.linalg.norm(y_pred-y)), aunque también retorno la predicción en caso de necesitarla.
Análisis de los Resultados
Al momento de inferencia se grafica la distribución de Errores por Norma L2 y el error para cada punto predicho. Por inspección visual se decide que todos los puntos con error mayor a 0.5 se consideran anomalías:
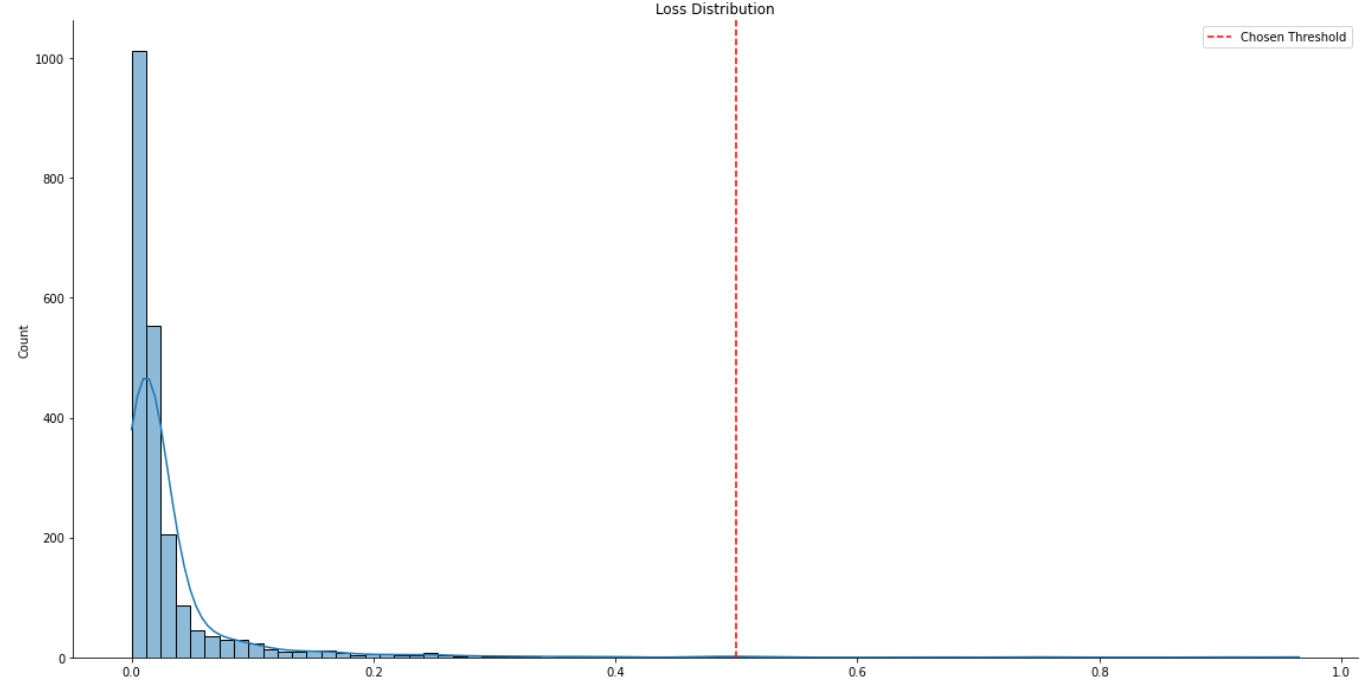
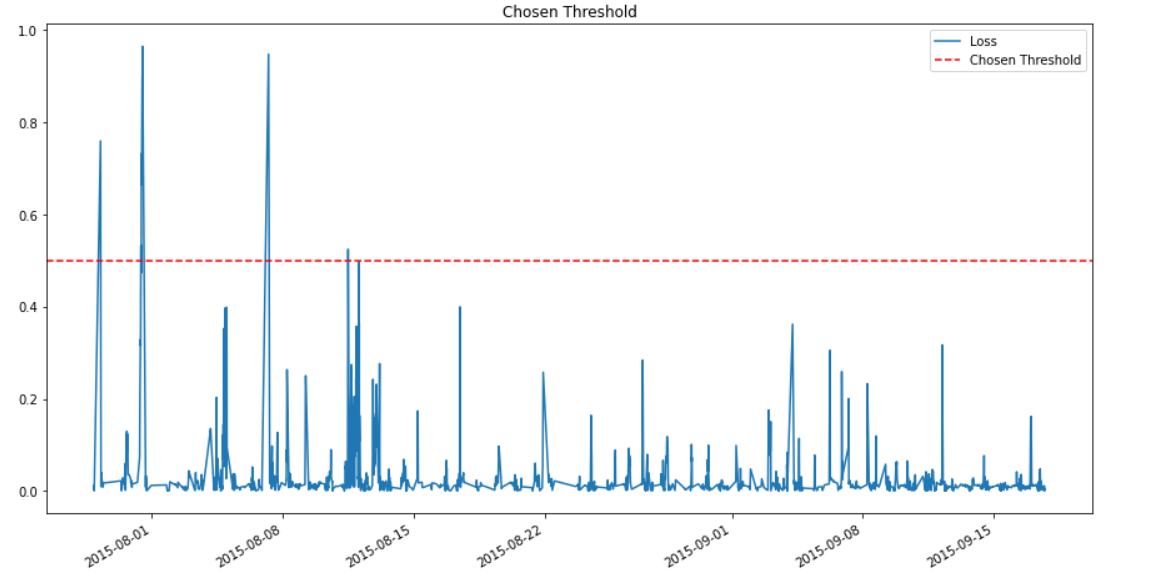
Anomalies Detected:
2015-07-29 06:49:00 0.759585
2015-07-31 10:29:00 0.504894
2015-07-31 10:39:00 0.533254
2015-07-31 10:59:00 0.509283
2015-07-31 11:09:00 0.731919
2015-07-31 11:29:00 0.665691
2015-07-31 11:39:00 0.734755
2015-07-31 11:59:00 0.815328
2015-07-31 12:09:00 0.890414
2015-07-31 12:29:00 0.904424
2015-07-31 12:33:00 0.965008
2015-08-07 06:09:00 0.947923
2015-08-11 12:07:00 0.524375
dtype: float32
Luego si marcamos los puntos encontrados en la serie de tiempo original obtenemos lo siguiente: 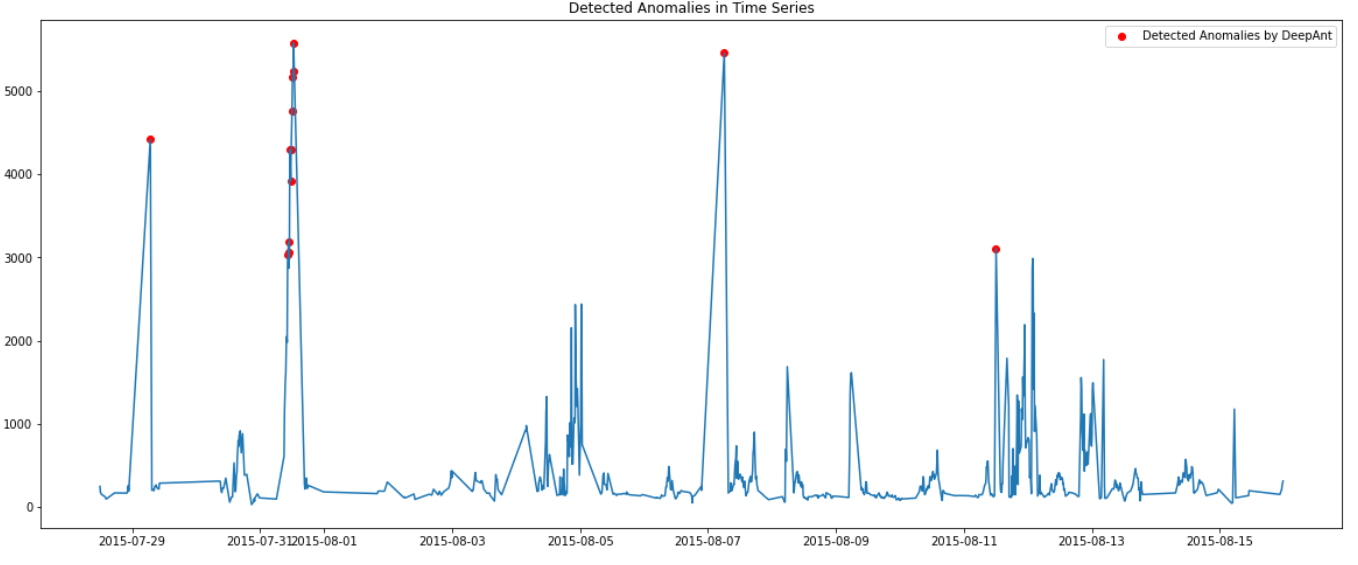
Bueno, no tenemos información sobre etiquetas existentes como para poder medir la performance del modelo. Esto debido a la naturaleza no supervisada del modelo. Lo que sí se indica en distintos blog post de este dataset es que existe una anomalía confirmada el día 2015-08-11 12:07:00. La cuál es difícil de detectar porque no es la más prominente de las existentes.
En este caso DeepAnt es capaz de encontrarla de manera exitosa junto con otras más.
Conclusiones
Es posible ver que DeepAnt funciona bastante bien. Es una arquitectura relativamente sencilla de realizar y su tiempo de entrenamiento e inferencia son bien bajos lo cual lo hace un modelo que puede ser de fácil implementación en producción.
- Ventajas: El uso de Redes Convolucionales 1D, ya que son mucho más fáciles de entrenar que una RNN, LSTM o GRU. Su procedimiento es estándar y fácilmente explicable.
- Desventajas: Debido a la naturaleza secuencial, no es posible detectar anomalías en los primeros
SEQ_LENpuntos, ya que no hay data previa para el Forecast necesario.
Bueno, espero que este tipo de modelos sean útiles tanto para eventualmente implementarlos como para aprender del funcionamiento del Deep Learning en Detección de Anomalías.
Y ahora a jugar con el modelo, no hay excusa. El código está para llegar y ejecutar en Colab!!!