Usando Pytorch para predecir Tarifas de Taxi en Nueva York
Redes Neuronales para Datos Tabulares
Cada vez me va gustando más Pytorch, por lo que me interesa ir probando nuevas cosas. La mayoría de mi trabajo requiere de datos tabulares (no hay mucho espacio en Chile para otro tipo de modelos aún) y es bien sabido que los modelo Boosting son el estado del Arte para este tipo de datos. ¿Pero es posible obtener buenos resultados utilizando redes neuronales en datos tabulares? Por supuesto que sí, ya hay ramas de investigación que están empezando a investigar entorno a esto. Una de estas ramas ya ha dado fruto creando Tabnet, que es la primera arquitectura de Redes Neuronales especializada en datos tabulares utilizando transformers (ver acá).
Hoy no entrenaremos un Tabnet (pero prometo hacerlo pronto), pero sí cómo enfrentar un problema de datos tabulares con variables categóricas y continuas utilizando Redes Neuronales. Para ello utilizaremos un dataset de Kaggle de un problema de Taxi en NYC.
En mi caso estoy utilizando un dataset reducido de 120000 registros, el cual disponibilizaré acá.
import torch
import torch.nn as nn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
En el caso de hoy estaré nuevamente entrenando la red en GPU en mi Laptop:
print(torch.cuda.is_available())
torch.cuda.get_device_name(0)
True
'GeForce RTX 2070 with Max-Q Design'
df = pd.read_csv('PYTORCH_NOTEBOOKS/Data/NYCTaxiFares.csv')
df.head()
| pickup_datetime | fare_amount | fare_class | pickup_longitude | pickup_latitude | dropoff_longitude | dropoff_latitude | passenger_count | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2010-04-19 08:17:56 UTC | 6.5 | 0 | -73.992365 | 40.730521 | -73.975499 | 40.744746 | 1 |
| 1 | 2010-04-17 15:43:53 UTC | 6.9 | 0 | -73.990078 | 40.740558 | -73.974232 | 40.744114 | 1 |
| 2 | 2010-04-17 11:23:26 UTC | 10.1 | 1 | -73.994149 | 40.751118 | -73.960064 | 40.766235 | 2 |
| 3 | 2010-04-11 21:25:03 UTC | 8.9 | 0 | -73.990485 | 40.756422 | -73.971205 | 40.748192 | 1 |
| 4 | 2010-04-17 02:19:01 UTC | 19.7 | 1 | -73.990976 | 40.734202 | -73.905956 | 40.743115 | 1 |
Target
El problema a tratar consiste en la predicción de la Tarifa que un Taxi en Nueva York cobrará. Para ello se puede ver que de 120000 viajes la Tarifa promedio ronda los US\$10 con un mínimo de US\$2.5 y Máximo de US\$49. Además la mediana está cerca de los US\$8.
df.fare_amount.describe()
count 120000.000000
mean 10.040326
std 7.500134
min 2.500000
25% 5.700000
50% 7.700000
75% 11.300000
max 49.900000
Name: fare_amount, dtype: float64
Feature Engineering
Se crearán variables derivadas a partir de los datos entregados en el dataset:
Distancia entre dos puntos
Para el cálculo de la distancia de dos puntos se utilizará la distancia Haversine. Para entender cómo funciona lo mejor es referirse a Wikipedia. La razón de esta formula es que es una fórmula que considera la curvatura de la tierra y se utiliza en especial para medir distancias cuando se tienen coordenadas geográficas.
A continuación una implementación en Python:
def haversine_distance(df, lat1, long1, lat2, long2):
r = 6371 # average radius of Earth in kilometers
phi1 = np.radians(df[lat1])
phi2 = np.radians(df[lat2])
delta_phi = np.radians(df[lat2]-df[lat1])
delta_lambda = np.radians(df[long2]-df[long1])
a = np.sin(delta_phi/2)**2 + np.cos(phi1) * np.cos(phi2) * np.sin(delta_lambda/2)**2
c = 2 * np.arctan2(np.sqrt(a), np.sqrt(1-a))
d = (r * c) # in kilometers
return d
df['dist_km'] = haversine_distance(df, 'pickup_latitude',
'pickup_longitude',
'dropoff_latitude',
'dropoff_longitude')
Variables temporales
A partir de la fecha de subida del pasajero es fácil obtener mucha información que puede ser importante al momento de estimar la tarifa:
df['pickup_datetime'] = df['pickup_datetime'].astype('datetime64')
df['EDTdate'] = df.pickup_datetime - pd.Timedelta(hours = 4)
Es importante notar que la zona horaria entregada en los datos es del tipo UTC. Si bien no soy un experto en zonas horarias, noté que esta no es la hora de NY, por lo tanto para entender de mejor manera los horarios preferidos por los pasajeros es mejor llevar la hora a la zona de Nueva York. Para aquello se restan 4 horas.
df['Hour'] = df.EDTdate.dt.hour
df['AMorPM'] = np.where(df.Hour>=12, 'PM','AM')
df['Weekday'] = df['EDTdate'].dt.strftime('%a') # day of the week
Modelamiento
Una vez creadas estas variables, es necesario definir cómo se tratará cada variable.
- Variables Categóricas: Hour, AMorPM, Weekday
- Variables Numéricas: pickup_longitude/latitude, dropoff_longitude/latitude, passenger_count y dist_km.
- Variable Target: fare_amount.
cat_cols = ['Hour','AMorPM','Weekday']
cont_cols = ['pickup_longitude',
'pickup_latitude', 'dropoff_longitude', 'dropoff_latitude',
'passenger_count', 'dist_km']
y_col = ['fare_amount']
df[cat_cols] = df[cat_cols].astype('category')
cats = df.select_dtypes('category').apply(lambda x: x.cat.codes).values
cont = df[cont_cols].values
cont
array([[-73.992365, 40.730521, -73.975499, 40.744746, 1. , 2.12631159],
[-73.990078, 40.740558, -73.974232, 40.744114, 1. , 1.39230687],
[-73.994149, 40.751118, -73.960064, 40.766235, 1. , 3.32676344],
...,
[-73.988574, 40.749772, -74.011541, 40.707799, 1. , 5.05252282],
[-74.004449, 40.724529, -73.992697, 40.730765, 1. , 1.20892296],
[-73.955415, 40.77192 , -73.967623, 40.763015, 1. , 1.42739869]])
cats = torch.tensor(cats, dtype = torch.int64)
cont = torch.tensor(cont, dtype = torch.float)
y = torch.tensor(df[y_col].values,dtype = torch.float)
Preprocesamiento (Embeddings).
Para lidiar con las variables categóricas se utilizarán embeddings. Esta representación es equivalente a un One Hot Encoding. Las variables categóricas serán definidas por un vector de dimensiones dadas por el modelador. La gracia de esta representación es que cada elemento del vector guarda características latentes de cada categoría lo cual permite establecer relaciones entre cada categoría. Esta representación no se entrega a la red, sino que ésta la aprende por sí misma en el proceso de entrenamiento.
Esto puede sonar un poco abstracto, pero es bien difícil de explicar. Espero poder explicar más en detalle qué es un embedding en futuros artículos. Ahora para elegir el número de dimensiones en el cual se quiere crear cada embedding se utilizará el siguiente criterio:
- Cada variable se reducirá al mínimo entre 50 y la mitad entera de sus variables.
cat_size = [len(df[col].cat.categories) for col in cat_cols]
emb_size = [(size, min(50,size+1)//2) for size in cat_size]
emb_size # corresponde al numero de categorías y el número al que se va a reducir
[(24, 12), (2, 1), (7, 4)]
En este caso, las horas son 24, por lo que se reducirán a 12 dimensiones, AM/PM se reducirá sólo a 1 y los días de la semana se reducirán a 4.
Para poder implementar esto en Pytorch básicamente se utiliza una capa de Embedding para cada variable categórica y los resultados se concatenarán.
El modelo propuesto es el siguiente:
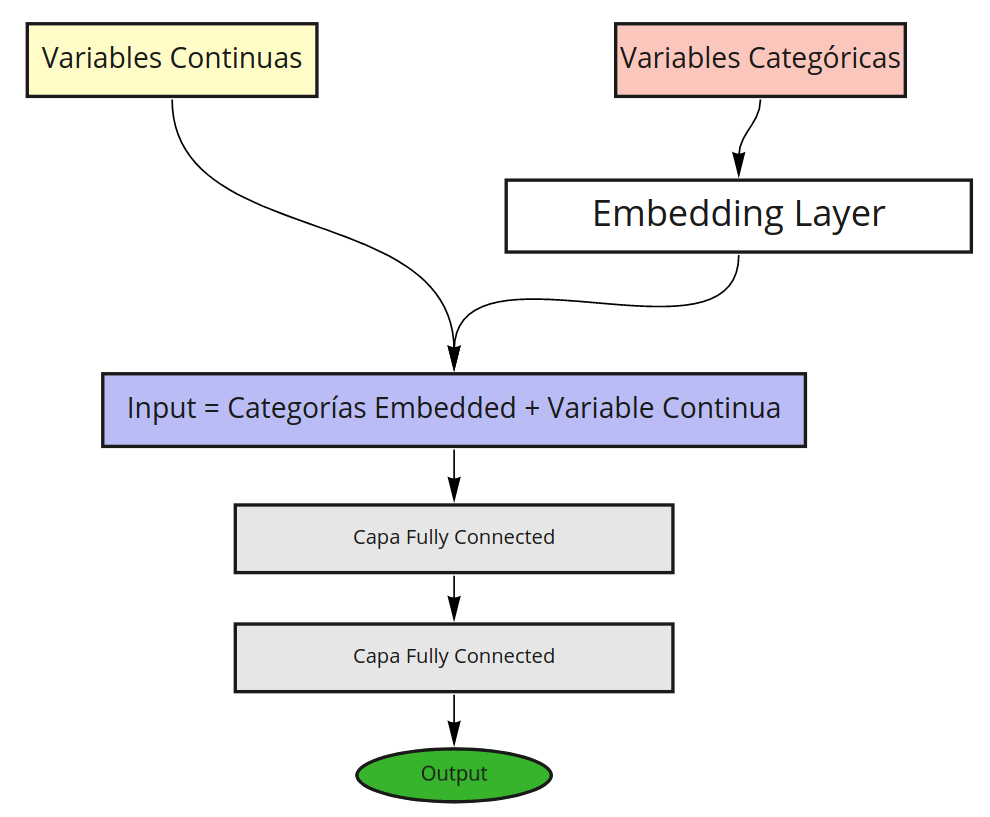
Implementación en Pytorch
def __init__(self,emb_szs, n_cont, out_sz, layers, p=0.5):
#layers = [200,100,50] unidades en cada capa
super().__init__()
self.embeds = nn.ModuleList([nn.Embedding(ni,nf) for ni,nf in emb_szs])
self.emb_drop = nn.Dropout(p)
self.bn_cont = nn.BatchNorm1d(n_cont)
layerlist = []
n_emb = sum([nf for ni,nf in emb_szs])
n_in = n_emb + n_cont
for i in layers:
layerlist.append(nn.Linear(n_in,i))
layerlist.append(nn.ReLU(inplace = True))
layerlist.append(nn.BatchNorm1d(i))
layerlist.append(nn.Dropout(p))
n_in = i
layerlist.append(nn.Linear(layers[-1],out_sz))
self.layers = nn.Sequential(*layerlist)
embedsserán los distintos embeddings para cada variable categórica. Como se puede ver, éstos irán reduciendo la dimensionalidad de acuerdo a lo determinado enemb_size. Esta capa embedding pasará por un dropout para su regularización.fcserá una capa secuencial que posee capas fully connected. Estas capas son dinámicas dependiendo de la lista entregada a través delayers. En el caso particular de esta red se crean dos secuencias de 200 y 100 neuronas cada una. Cada secuencia se co\$
def forward(self, x_cat, x_cont):
embeddings = []
for i,e in enumerate(self.embeds):
embeddings.append(e(x_cat[:,i]))
x = torch.cat(embeddings,1)
x = self.emb_drop(x)
x_cont = self.bn_cont(x_cont)
x = torch.cat([x,x_cont],1)
x = self.fc(x)
return x
En el caso del Forward Propagation es bastante directo:
- Cada variable categórica pasará por su embedding correspondiente y los resultados se concatenarán.
- Estos embeddings son regularizados mediante Dropout (
emb_drop) mientras que las variables continuas pasarán por un Batch Normalization (bn_cont). - Variales continuas y Embeddings se concatenan para luego conectarse a las secuencias fully connected de 200 y 100 neuronas.
- Finalmente se conecta con una única neurona de salida sin activación que será la responsable de estimar la tarifa final.
class TabularModel(nn.Module):
def __init__(self,emb_szs, n_cont, out_sz, layers, p=0.5):
#layers = [200,100,50] unidades en cada capa
super().__init__()
self.embeds = nn.ModuleList([nn.Embedding(ni,nf) for ni,nf in emb_szs])
self.emb_drop = nn.Dropout(p)
self.bn_cont = nn.BatchNorm1d(n_cont)
layerlist = []
n_emb = sum([nf for ni,nf in emb_szs])
n_in = n_emb + n_cont
for i in layers:
layerlist.append(nn.Linear(n_in,i))
layerlist.append(nn.ReLU(inplace = True))
layerlist.append(nn.BatchNorm1d(i))
layerlist.append(nn.Dropout(p))
n_in = i
layerlist.append(nn.Linear(layers[-1],out_sz))
self.fc = nn.Sequential(*layerlist)
def forward(self, x_cat, x_cont):
embeddings = []
la
x_cont = self.bn_cont(x_cont)
x = torch.cat([x,x_cont],1)
x = self.fc(x)
return x
torch.manual_seed(33)
model = TabularModel(emb_size, n_cont = cont.shape[1],out_sz = 1,layers = [200,100],p = 0.4)
model
TabularModel(
(embeds): ModuleList(
(0): Embedding(24, 12)
(1): Embedding(2, 1)
(2): Embedding(7, 4)
)
(emb_drop): Dropout(p=0.4, inplace=False)
(bn_cont): BatchNorm1d(6, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(layers): Sequential(
(0): Linear(in_features=23, out_features=200, bias=True)
(1): ReLU(inplace=True)
(2): BatchNorm1d(200, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(3): Dropout(p=0.4, inplace=False)
(4): Linear(in_features=200, out_features=100, bias=True)
(5): ReLU(inplace=True)
(6): BatchNorm1d(100, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(7): Dropout(p=0.4, inplace=False)
(8): Linear(in_features=100, out_features=1, bias=True)
)
)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
gpumodel = model.to(device)
torch.cuda.memory_allocated()
113664
Entrenamiento
Una vez generado el modelo a utilizar se procede a la definición del proceso de entrenamiento. Debido a que se trata de un modelo de Regresión ya que se busca estimar un valor de Tarifa que es continuo es que se utilizará MSE como Loss y Adam como optimizador
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr = 0.001)
Asumiendo que los datos ya se encuentran mezclados, se tomará un 20% para testear. El entrenamiento en este caso se realizará full batch.
batch_size = 120000
test_size = int(0.2*batch_size)
cat_train = cats[:batch_size-test_size].to(device)
cat_test = cats[batch_size-test_size:batch_size].to(device)
con_train = cont[:batch_size-test_size].to(device)
con_test = cont[batch_size-test_size:batch_size].to(device)
y_train = y[:batch_size-test_size].to(device)
y_test = y[batch_size-test_size:batch_size].to(device)
Se utilizarán entonces 96000 muestras para entrenar y 24000 para validar. Además debido a que el entrenamiento es full batch se pasarán todos los datos directament a la GPU.
Cuidado al entrenar full batch, en este caso los datos caben en la memoria de la GPU por lo que no hay problema, en caso de tener datos muy masivos que no caben, será entonces necesarios utilizar DataLoaders y entrenar en estrategia mini batch.
import time
start_time = time.time()
epochs = 300
losses = []
for i in range(epochs):
i +=1
y_pred = gpumodel(cat_train, con_train)
loss = torch.sqrt(criterion(y_pred, y_train))
losses.append(loss)
if i%10 == 0:
print(f'epoch {i} loss is {loss}')
optimizer.zero_grad()
loss.backward()
optimizer.step()
duration = time.time()- start_time
print(f'Training took {duration/60} minutes')
epoch 1 loss is 12.594930648803711
epoch 11 loss is 11.699335098266602
epoch 21 loss is 11.113286018371582
epoch 31 loss is 10.731647491455078
epoch 41 loss is 10.447735786437988
epoch 51 loss is 10.237385749816895
epoch 61 loss is 10.032994270324707
epoch 71 loss is 9.844207763671875
epoch 81 loss is 9.644638061523438
epoch 91 loss is 9.422845840454102
epoch 101 loss is 9.169548988342285
epoch 111 loss is 8.881169319152832
epoch 121 loss is 8.556023597717285
epoch 131 loss is 8.199341773986816
epoch 141 loss is 7.798142910003662
epoch 151 loss is 7.363061904907227
epoch 161 loss is 6.910421371459961
epoch 171 loss is 6.424202919006348
epoch 181 loss is 5.949601650238037
epoch 191 loss is 5.45380973815918
epoch 201 loss is 4.996823310852051
epoch 211 loss is 4.616281986236572
epoch 221 loss is 4.32720422744751
epoch 231 loss is 4.067756175994873
epoch 241 loss is 3.9491124153137207
epoch 251 loss is 3.842698335647583
epoch 261 loss is 3.816580057144165
epoch 271 loss is 3.772189140319824
epoch 281 loss is 3.70717453956604
epoch 291 loss is 3.703880786895752
Training took 0.4332761804262797 minutes
Podemos notar que el proceso fue un éxito, en poco menos de 30 segundos entrenamos cerca de 100000 datos por 300 epochs. Los resultados son bastante alentadores ya que el enunciado de Kaggle habla de que normalemente se esperan resultados de RMSE del orden de US\$5-US\$8 y obtuvimos bajo US\$4, lo cual es muy bueno.
Si evaluamos ahora el RMSE en el set de Test logramos incluso menos de US\$3. Lo cual me deja bastante conforme.
model.eval()
with torch.no_grad():
y_val = model(cat_test, con_test)
loss = torch.sqrt(criterion(y_val, y_test))
loss
tensor(2.9336, device='cuda:0')
Acá se pueden ver como anduvieron las primeras 10 predicciones:
for i in range(10):
print(f'{i+1}.) PREDICTED: {y_val[i].item():8.2f} TRUE: {y_test[i].item():.2f}')
1.) PREDICTED: 3.84 TRUE: 2.90
2.) PREDICTED: 22.68 TRUE: 5.70
3.) PREDICTED: 6.32 TRUE: 7.70
4.) PREDICTED: 13.50 TRUE: 12.50
5.) PREDICTED: 5.09 TRUE: 4.10
6.) PREDICTED: 5.37 TRUE: 5.30
7.) PREDICTED: 4.80 TRUE: 3.70
8.) PREDICTED: 17.40 TRUE: 14.50
9.) PREDICTED: 5.49 TRUE: 5.70
10.) PREDICTED: 11.72 TRUE: 10.10
Si bien, falta para que las redes neuronales destronen a los algoritmos de Gradient Boosting en términos de performance en data tabular, es posible hacer modelos con Arquitecturas no tan tradicionales que permiten entregar buenos resultados.
Espero les haya gustado y aprendido algo nuevo, porque yo aprendí harto.
