Implementando un algoritmo de Anomaly Detection
Anomalías cardiacas con Deep Learning
Siguiendo con los tutoriales de aplicaciones poco convencionales hoy quiero presentar un tipo de tarea distinta: Anomaly Detection. Este es quizás uno de las aplicaciones con más proyección dentro del Machine Learning por varias cosas…
- Primero, se trata de aprendizaje no supervisado. Uno de los grandes dolores de la inteligencia artificial es la falta de data correctamente etiquetada y este tipo de tareas no requiere de ellas.
- Incluso teniendo data etiquetada la prevalencia de fenómenos inusuales es tan baja que no permitiría aprender lo suficiente a un modelo de clasificación convencional.
- Este tipo de técnica en particular permite reconstruir patrones que probablemente no son muy claros ni siquiera para expertos en el área.
Es por eso que encontré este desafío que me pareció bien interesante, que es la detección de latidos cardiacos anómalos. Para ello se dispone de data extraída de exámenes de Electrocardiograma, los cuales hasta donde entiendo son capaces de detectar afecciones cardiacas midiendo los impulsos electricos del corazón.
No soy para nada un experto en temas médicos y menos cardiacos. Sé que dentro de mi red hay algunas personas que se dedican al análisis de datos en Medicina y quiero pedirles de antemano si ven alguna aberración de mi parte, y en caso de que tengan alguna sugerencia de mejora del modelo estoy sumamente abierto a conversarlo.
Importación de Librerías
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc
from sklearn.model_selection import train_test_split
from arff2pandas import a2p
import glob
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from multiprocessing import cpu_count
from pytorch_lightning.callbacks import ModelCheckpoint
import pytorch_lightning as pl
sns.set(style = 'whitegrid', palette = 'muted', font_scale = 1.2)
HAPPY_COLORS_PALETTE = ["#01BEFE", "#FFDD00", "#FF7D00", "#FF006D", "#ADFF02", "#8F00FF"]
sns.set_palette(sns.color_palette(HAPPY_COLORS_PALETTE))
RANDOM_SEED = 42
pl.seed_everything(RANDOM_SEED)
Global seed set to 42
Importando los Datos
En caso de que les interese reproducir el ejercicio, pueden obtener los datos desde acá.
Lo interesante de este problema es que la data viene en un tipo de formato que no había visto antes que es el .arff. Afortunadamente existe una librería en Python llamada arff2pandas que permite lidiar con este formato de archivo y transformarlo directamente en un DataFrame de Pandas.
with open('ECG5000/ECG5000_TRAIN.arff') as f:
train = a2p.load(f)
train.head()
| att1@NUMERIC | att2@NUMERIC | att3@NUMERIC | att4@NUMERIC | att5@NUMERIC | att6@NUMERIC | att7@NUMERIC | att8@NUMERIC | att9@NUMERIC | att10@NUMERIC | ... | att132@NUMERIC | att133@NUMERIC | att134@NUMERIC | att135@NUMERIC | att136@NUMERIC | att137@NUMERIC | att138@NUMERIC | att139@NUMERIC | att140@NUMERIC | target@{1,2,3,4,5} | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.112522 | -2.827204 | -3.773897 | -4.349751 | -4.376041 | -3.474986 | -2.181408 | -1.818286 | -1.250522 | -0.477492 | ... | 0.792168 | 0.933541 | 0.796958 | 0.578621 | 0.257740 | 0.228077 | 0.123431 | 0.925286 | 0.193137 | 1 |
| 1 | -1.100878 | -3.996840 | -4.285843 | -4.506579 | -4.022377 | -3.234368 | -1.566126 | -0.992258 | -0.754680 | 0.042321 | ... | 0.538356 | 0.656881 | 0.787490 | 0.724046 | 0.555784 | 0.476333 | 0.773820 | 1.119621 | -1.436250 | 1 |
| 2 | -0.567088 | -2.593450 | -3.874230 | -4.584095 | -4.187449 | -3.151462 | -1.742940 | -1.490659 | -1.183580 | -0.394229 | ... | 0.886073 | 0.531452 | 0.311377 | -0.021919 | -0.713683 | -0.532197 | 0.321097 | 0.904227 | -0.421797 | 1 |
| 3 | 0.490473 | -1.914407 | -3.616364 | -4.318823 | -4.268016 | -3.881110 | -2.993280 | -1.671131 | -1.333884 | -0.965629 | ... | 0.350816 | 0.499111 | 0.600345 | 0.842069 | 0.952074 | 0.990133 | 1.086798 | 1.403011 | -0.383564 | 1 |
| 4 | 0.800232 | -0.874252 | -2.384761 | -3.973292 | -4.338224 | -3.802422 | -2.534510 | -1.783423 | -1.594450 | -0.753199 | ... | 1.148884 | 0.958434 | 1.059025 | 1.371682 | 1.277392 | 0.960304 | 0.971020 | 1.614392 | 1.421456 | 1 |
5 rows × 141 columns
with open('ECG5000/ECG5000_TEST.arff') as f:
test = a2p.load(f)
test.head()
| att1@NUMERIC | att2@NUMERIC | att3@NUMERIC | att4@NUMERIC | att5@NUMERIC | att6@NUMERIC | att7@NUMERIC | att8@NUMERIC | att9@NUMERIC | att10@NUMERIC | ... | att132@NUMERIC | att133@NUMERIC | att134@NUMERIC | att135@NUMERIC | att136@NUMERIC | att137@NUMERIC | att138@NUMERIC | att139@NUMERIC | att140@NUMERIC | target@{1,2,3,4,5} | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.690844 | 0.711414 | -2.114091 | -4.141007 | -4.574472 | -3.431909 | -1.950791 | -1.107067 | -0.632322 | 0.334577 | ... | 0.022847 | 0.188937 | 0.480932 | 0.629250 | 0.577291 | 0.665527 | 1.035997 | 1.492287 | -1.905073 | 1 |
| 1 | -1.348132 | -3.996038 | -4.226750 | -4.251187 | -3.477953 | -2.228422 | -1.808488 | -1.534242 | -0.779861 | -0.397999 | ... | 1.570938 | 1.591394 | 1.549193 | 1.193077 | 0.515134 | 0.126274 | 0.267532 | 1.071148 | -1.164009 | 1 |
| 2 | 1.024295 | -0.590314 | -1.916949 | -2.806989 | -3.527905 | -3.638675 | -2.779767 | -2.019031 | -1.980754 | -1.440680 | ... | 0.443502 | 0.827582 | 1.237007 | 1.235121 | 1.738103 | 1.800767 | 1.816301 | 1.473963 | 1.389767 | 1 |
| 3 | 0.545657 | -1.014383 | -2.316698 | -3.634040 | -4.196857 | -3.758093 | -3.194444 | -2.221764 | -1.588554 | -1.202146 | ... | 0.777530 | 1.119240 | 0.902984 | 0.554098 | 0.497053 | 0.418116 | 0.703108 | 1.064602 | -0.044853 | 1 |
| 4 | 0.661133 | -1.552471 | -3.124641 | -4.313351 | -4.017042 | -3.005993 | -1.832411 | -1.503886 | -1.071705 | -0.521316 | ... | 1.280823 | 1.494315 | 1.618764 | 1.447449 | 1.238577 | 1.749692 | 1.986803 | 1.422756 | -0.357784 | 1 |
5 rows × 141 columns
Debido a que vamos a plantear esto como un problema de Detección de Anomalías no supervisado no vamos a depender de las etiquetas. Por lo tanto para poder tener más datos para que el modelo aprenda vamos a unir los datasets de train y test y mezclarlos de la siguiente forma:
df = train.append(test)
df = df.sample(frac=1) # equivale a un shuffle
train.shape, test.shape, df.shape
((500, 141), (4500, 141), (5000, 141))
Haciendo mis averiguaciones (mi hermano está terminando su internado en Medicina), obtuve lo siguiente:
- El Electocardiograma (ECG para los amigos) mide la señal eléctrica del corazón (perdón si no utilizo la terminología apropiada) para detectar afecciones cardiacas.
- El ECG es uno de los exámenes más complejos de poder interpretar ya que las diferencias requieren mucha experiencia.
- Se requiere de médicos cardiólogos altamente especializados para poder leerlos de buena manera. E incluso a ellos les puede costar.
Un ECG se ve así:
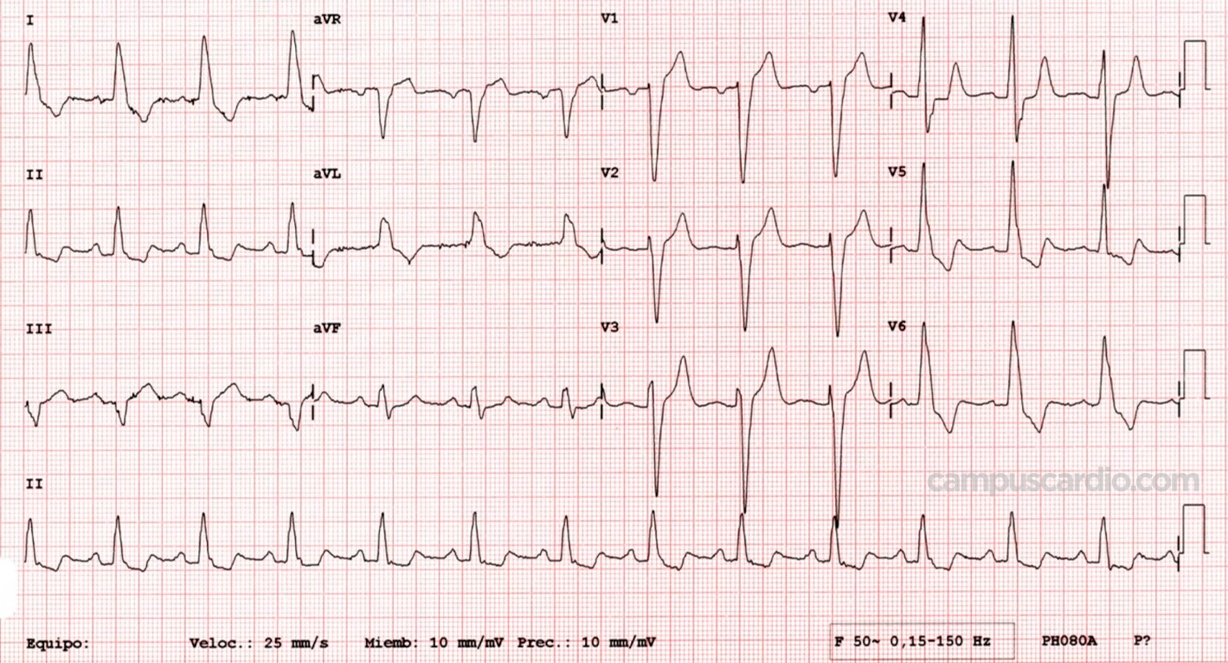
La data utilizada no son ECG si no que en realidad corresponden a 500 latidos extraídos de alreadedor de 20 horas de ECG. Cada uno de estos latidos fueron clasificados de la siguiente manera:
- Normal (N)
- R on T Premature Ventricular Contraction (R-on-T PVC)
- Premature Ventricular Contraction (PVC)
- Supra Ventricular Premature or Ectopic Beat (SP or EB)
- Unclassified Beat (UB)
Si alguien sabe qué significan estos diagnósticos, les agradecería enormemente para poder entender el contexto del problema. Si bien le pregunté a mi hermano, no es cardiologo, por lo que no estaba tan familiarizado con estos conceptos.
Exploración de los Datos
Como se puede ver los nombres de las columnas son un poco extraños. Al parecer esto se debe por el tipo de dato extraño del cual estamos importando. Para facilitar la manipulación de los datos vamos a cambiar el nombre de nuestro vector de Labels. Si bien no lo vamos a utilizar para el proceso de entrenamiento sí lo utilizaremos para separar la data normal de la anómala para que nuestro modelo pueda aprender.
new_columns = df.columns.tolist()
new_columns[-1] = 'target'
df.columns = new_columns
df.columns
Index(['att1@NUMERIC', 'att2@NUMERIC', 'att3@NUMERIC', 'att4@NUMERIC',
'att5@NUMERIC', 'att6@NUMERIC', 'att7@NUMERIC', 'att8@NUMERIC',
'att9@NUMERIC', 'att10@NUMERIC',
...
'att132@NUMERIC', 'att133@NUMERIC', 'att134@NUMERIC', 'att135@NUMERIC',
'att136@NUMERIC', 'att137@NUMERIC', 'att138@NUMERIC', 'att139@NUMERIC',
'att140@NUMERIC', 'target'],
dtype='object', length=141)
Lo importante de entender acá es que cada fila corresponde a una secuencia (una serie de tiempo) que interpreta una señal eléctrica de un latido cardiaco en 140 instantes. La fila 141 correponde al diagnostico dado a ese latido que sigue la siguiente nomenclatura:
CLASS_NORMAL = 1
class_names = ['Normal','R on T','PVC','SP','UB']
ax = df.target.value_counts().plot(kind = 'bar')
ax.set_xticklabels(class_names);
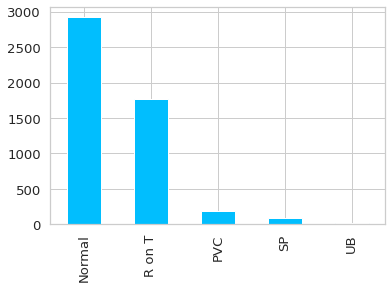
Lo primero que se puede apreciar es que las anomalías se dan en bastante menor medida que los datos normales (quizás la excepción es el R on T). Lo cual es bueno, ya que de no ser así no serían anomalías.
Adicionalmente poder ver la data de manera apropiada es importante. Por lo tanto para poder entender “en promedio” cómo se ven los distintos diagnósticos de un latido usaremos lo siguiente:
def plot_time_series_class(data, class_name, ax, n_steps=10):
time_series_df = pd.DataFrame(data)
smooth_path = time_series_df.rolling(n_steps).mean()
path_deviation = 2 * time_series_df.rolling(n_steps).std()
under_line = (smooth_path - path_deviation)[0]
over_line = (smooth_path + path_deviation)[0]
ax.plot(smooth_path, linewidth=2)
ax.fill_between(
path_deviation.index,
under_line,
over_line,
alpha=.125
)
ax.set_title(class_name)
classes = df.target.unique()
fig, axs = plt.subplots(nrows = len(classes)// 3 + 1,
ncols = 3,
sharey = True,
figsize = (12,8)
)
for i, cls in enumerate(classes):
ax = axs.flat[i]
data = df.query(f'target == "{cls}"').drop(columns = 'target').mean(axis = 0).to_numpy()
plot_time_series_class(data, class_names[i], ax)
fig.delaxes(axs.flat[-1])
fig.tight_layout();
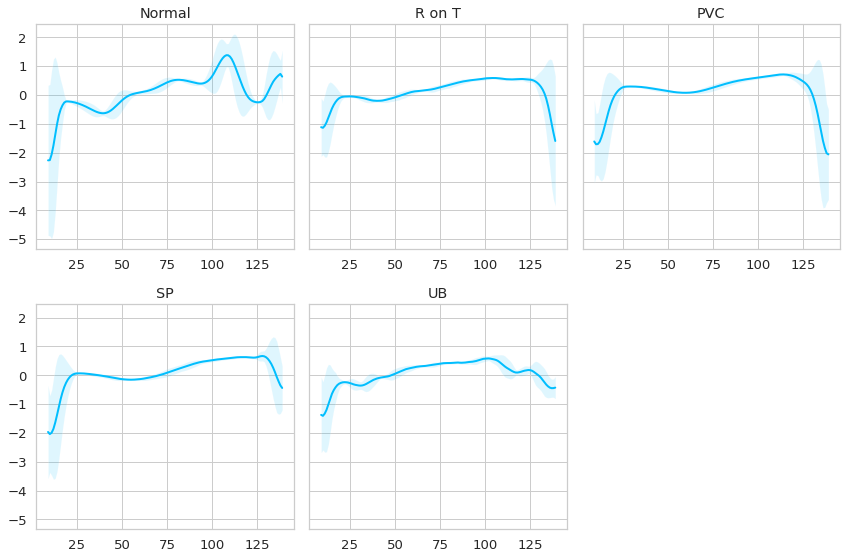
Observando los datos se puede apreciar lo siguiente:
Los latidos normales se caracterizan por un incremento de la señal inicialmente y luego un peak y un valle al final del latido.
Las anomalías se caracterizan porque no tienen ese peak al final, y rapidamente la señal decae, probablemente con distintas intensidades dependiendo de la anomalía. Quizás se requiere de un ojo más experto para poder diferenciar de mejor manera las distintas afecciones anómalas, pero para nuestro caso basta con que las anomalías equivalen a
“no-normal”
.
Data Split
Si bien en este caso juntamos toda la data disponible para tener más muestras de entrenamiento, eso no significa que no la dividiremos. Además nuestro modelo no aprenderá utilizando Etiquetas, sino que aprenderá lo “normal”
para luego detectar que algo no está dentro de lo normal.
La manera en la que separaremos los datos es la siguiente:
- normal_data: Contendrá toda la data clasificada como normal. Este dataset será posteriormente** dividido en train_df, val_df y test_df.
- anomaly_df: Contendrá toda la data que NO está clasificada como normal, las anomalías.
Creación del modelo en Pytorch Lightning
Como ya sabemos de tutoriales anteriores, el modelo en Pytorch Lightning parte generando la clase Dataset y el LightningDataModule. Estos procesos transformarán la data en tensores para que puedan ser procesados por Pytorch.
La clase ECGData transformará cada fila de los dataframes en tensores que representan una serie de tiempo de un latido.
La clase ECGDataModule define varios métodos:
import_arffes una utility function que importa un dataset del formato arff a pandas.setup: Es el el método encargado de organizar todas las fuentes de datos del modelo:- Importa los archivos terminados en .arff y los concatena como un sólo pandas DataFrame.
- Se define el
normal_datacomo el DataFrame que contiene sólo latidos de clase normal. - Se utiliza un split para separar normal_data en
train_df,val_dfytest_df. - Se define
anomaly_dfcomo todos los latidos que no contienen una clase normal. - Se transforman los distintos
dfcreados en tensores utilizando la clase ECGData. Es sumamente importante destacar que ninguno de los dataset incluirá el target asociado. El modelo sólo aprenderá lo normal, esperando que pueda diferenciar lo anómalo.
- Finalmente se crean los
DataLoaderscorrespondientes para cada subset.- Se considera el
predict_dataloadercon la data de anomalías.
- Se considera el
class ECGData(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
# agrega singleton dim al final. dtype debe ser float ya que es el requerido por LSTMs.
return torch.tensor(self.data.iloc[idx], dtype = torch.float32).unsqueeze(-1)
class ECGDataModule(pl.LightningDataModule):
def __init__(self, folder_path, normal_class, test_splits = [0.15, 0.5], batch_size = 1):
super().__init__()
self.folder_path = folder_path
self.normal_class = normal_class
self.batch_size = batch_size
self.val_split, self.test_split = test_splits
def import_arff(self, path):
with open(path) as f:
data = a2p.load(f)
return data
def setup(self, stage = None):
file_paths = glob.glob(f'{self.folder_path}/*.arff')
self.data = pd.concat([self.import_arff(f) for f in file_paths]).rename(columns = {'target@{1,2,3,4,5}': 'target'})
normal_data = self.data.query(f'target == "{self.normal_class}"').drop(columns = 'target')
self.train_df, self.val_df = train_test_split(normal_data, test_size = self.val_split, random_state=RANDOM_SEED)
self.val_df, self.test_df = train_test_split(self.val_df, test_size = self.test_split, random_state=RANDOM_SEED)
self.anomaly_df = self.data.query(f'target != "{self.normal_class}"').drop(columns = 'target')
self.train_df = ECGData(self.train_df)
self.val_df = ECGData(self.val_df)
self.test_df = ECGData(self.test_df)
self.anomaly_df = ECGData(self.anomaly_df)
def train_dataloader(self):
return DataLoader(self.train_df, batch_size = self.batch_size, pin_memory = True, num_workers = cpu_count(), shuffle=False)
def val_dataloader(self):
return DataLoader(self.val_df, batch_size = self.batch_size, pin_memory = True, num_workers = cpu_count(), shuffle=False)
def test_dataloader(self):
return DataLoader(self.test_df, batch_size = self.batch_size, pin_memory = True, num_workers = cpu_count(), shuffle=False)
def predict_dataloader(self):
return DataLoader(self.anomaly_df, batch_size = 1, pin_memory = True, num_workers = cpu_count(), shuffle=False)
dm = ECGDataModule('ECG5000', normal_class = 1, batch_size = 100)
dm.setup()
dm.train_df[0].shape
torch.Size([140, 1])
Como podemos ver, para poder ingresar la data con las dimensiones correctas se agregó un singleton al final. De esta manera se reconoce que el tensor es de largo 140 y contiene sólo una dimensión asociada a features (es univariado). Esto para cumplir los requerimientos de dimensiones de las Redes LSTM que son las que vamos a utilizar.
for batch in dm.train_dataloader():
print(batch.shape)
break
torch.Size([100, 140, 1])
Además si ejecutamos una instancia del DataLoader podemos ver las dimensiones del tensor resultante: 100 muestras, de tamaño 140 (largo de la secuencia) por 1 (una variable).
El modelo propiamente tal
El modelo que utilizaremos en un LSTM AutoEncoder. La implementación está basada en la utilizada acá por sequitur.
Partamos definiendo qué es un autoencoder. Un autoencoder es una arquitectura de Redes Neuronales que permite recrear una data de entrada. La data se intenta pasar por un embedding que actúa como cuello de botella con la intención de la red pueda extraer sólo las características esenciales. El embedding viene a ser la representación de la data en un espacio alternativo, normalmente reducido (por eso el cuello de botella).Replicar la secuencia original a partir de este espacio reducido forzará a la red a replicar sólo lo esencial de la secuencia.
Normalmente se considera que el output de un Autoencoder es equivalente a una reducción de dimensionalidad no supervisada o un denoiser. La premisa en este tipo de modelos es que la red aprenderá a reconstruir ECG “normales”. La reconstrucción de un ECG normal debiera ser muy similar al real, es decir, el error será pequeño. Pero si la red intenta reconstruir un ECG que no es normal, entonces el error será mayor. Ajustando la red a un threshold de error podemos detectar cuales son los outliers de nuestra distribución de errores, los que serán catalogados como anomalías.
Con respecto a la arquitectura, existen muchos tipos distintos de Autoencoders, para resolver este problema en particular consideré que un LSTM AutoEncoder es apropiado ya que permite recrear secuencias univariadas, como es el caso a resolver. Éste, tendrá el objetivo de tomar un conjunto de secuencias a las que reducirá su dimensionalidad hasta llegar al cuello de botella z(n). Este será el resultado del hidden state de la útlima LSTM usada en la parte Encoder del Modelo.
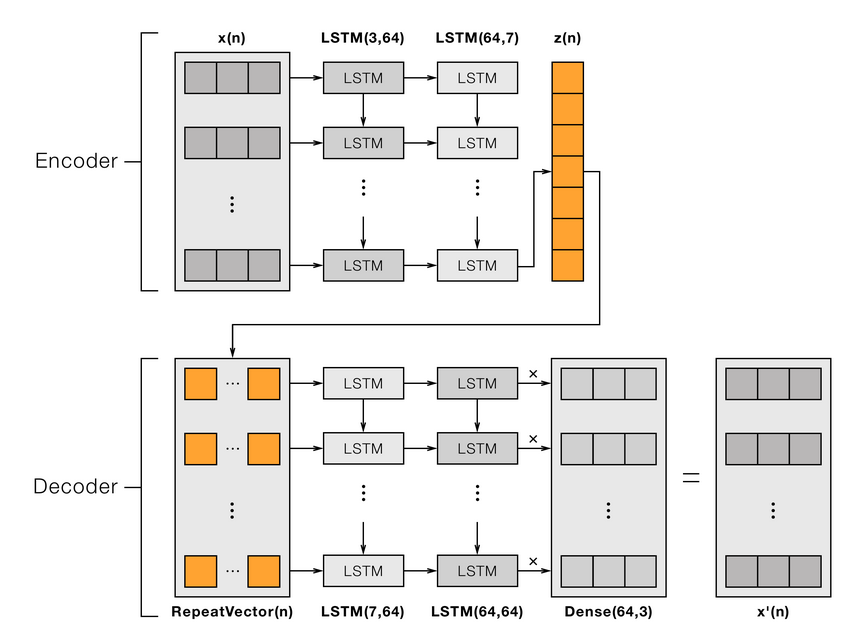
Este cuello de botella z(n) se repetirá tantas veces como el largo de secuencia inicial y se someterá a un Decoder también formado por LSTMs. A diferencia del Encoder acá el output total de las LSTMs usadas, la cual pasará por una capa fully connected para reconstruir la dimensión inicial de la secuencia.
Mucho de lo que se verá acá es implementación propia. Primero, no he visto implementaciones en Pytorch Lightning de esto, por lo que la traducción la hice yo. Además la implementación en la que me basé estaba diseñada sólo para entrenar con un batch_size de 1. Esto generaba que el entrenamiento fuera extremadamente lento. Por eso me tomé la libertad de modificar el Encoder y el Decoder para que pudiera realizarse un entrenamiento en Batch. Úselo con cuidado, y si encuentra algun error en mi implementación no dude en señalarlo.
class Encoder(nn.Module):
def __init__(self, seq_len, n_features, embedding_dim = 64):
super().__init__()
self.n_features = n_features
self.embedding_dim, self.hidden_dim = embedding_dim, 2 * embedding_dim
self.seq_len = seq_len
self.rnn1 = nn.LSTM(
input_size = n_features,
hidden_size = self.hidden_dim,
num_layers = 1,
batch_first = True
)
self.rnn2 = nn.LSTM(
input_size = self.hidden_dim,
hidden_size = self.embedding_dim,
num_layers = 1,
batch_first = True
)
def forward(self, x):
x = x.reshape((-1, self.seq_len, self.n_features))
x, (hidden_n, cell_n) = self.rnn1(x)
x, (hidden_n, cell_n) = self.rnn2(x)
return hidden_n.reshape((-1, self.embedding_dim)) #.squeeze(0)#
El Encoder entonces espera el largo de la secuencia (140), el número de features (1) y una dimensión de embedding de 64, que será la dimensión del cuello de botella. En este caso nuestro decoder tomará las 140 secuencias, las reducirá a 128 y luego a 64. Dado que usamos este orden de dimensiones debemos agregar el parámetro batch_first = True.
class Decoder(nn.Module):
def __init__(self, seq_len, input_dim = 64, output_dim = 1):
super().__init__()
self.seq_len = seq_len
self.input_dim = input_dim
self.output_dim = output_dim
self.hidden_dim = 2* input_dim
self.rnn1 = nn.LSTM(
input_size = input_dim,
hidden_size = input_dim,
num_layers = 1,
batch_first = True
)
self.rnn2 = nn.LSTM(
input_size = input_dim,
hidden_size = self.hidden_dim,
num_layers = 1,
batch_first = True
)
self.dense_layers = nn.Linear(self.hidden_dim, output_dim)
def forward(self, x):
x = x.repeat(self.seq_len, 1) # Capa de Repetición
x = x.reshape((-1, self.seq_len, self.input_dim)) # Reshaping para aceptar data en batch
x, (hidden_n, cell_n) = self.rnn1(x)
x, (hidden_n, cell_n) = self.rnn2(x)
return self.dense_layers(x)
En el caso del Decoder tomará un tensor proveniente del Encoder, de largo de secuencia 64 (por el embedding), lo repetirá simulando el largo de secuencia original y aumentará su dimensión hasta llegar a las dimensiones originales.
Notar que si hacemos el feed forward de un batch de secuencias, a la salida del Encoder está la secuencias reducidas al embedding y luego a la salida del Decoder vuelve al tamaño original, es decir, el AutoEncoder efectivamente es capaz de recontruir las secuencias entregadas al inicio.
enc = Encoder(seq_len = 140, n_features = 1)
dec = Decoder(seq_len = 140)
for batch in dm.train_dataloader():
print('Tamaño del Batch Inicial:', batch.shape)
x = enc(batch)
print('Tamaño a la Salida del Encoder:', x.shape)
print('Tamaño a la Salida del Decoder:', dec(x).shape)
break
Tamaño del Batch Inicial: torch.Size([100, 140, 1])
Tamaño a la Salida del Encoder: torch.Size([100, 64])
Tamaño a la Salida del Decoder: torch.Size([100, 140, 1])
Finalmente se combinan Encoder y Decoder para crear la arquitectura final en el LightningModule. Se define como criterio para medir el error el L1Loss y como optimizador un Adam con learning_rate de 1e-3.
class LSTMAutoEncoder(pl.LightningModule):
def __init__(self, seq_len = 140, n_features = 1):
super().__init__()
self.encoder = Encoder(seq_len, n_features)
self.decoder = Decoder(seq_len)
self.criterion = nn.L1Loss(reduction = 'mean')
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
def training_step(self, batch, batch_idx):
pred_seq = self(batch)
loss = self.criterion(pred_seq, batch)
self.log('train_loss', loss, prog_bar = True)
return loss
def validation_step(self, batch, batch_idx):
pred_seq = self(batch)
loss = self.criterion(pred_seq, batch)
self.log('val_loss', loss, prog_bar = True)
def predict_step(self, batch, batch_idx, dataloader_idx = None):
pred_seq = self(batch)
loss = self.criterion(pred_seq, batch)
return pred_seq, loss
def configure_optimizers(self):
return torch.optim.Adam(self.parameters(), lr = 1e-3)
Entrenamiento del Modelo
Luego de crear la arquitectura vamos a instanciar el modelo junto con el LightningDataModule. Generaremos además un ModelCheckpoint guardando los modelos que tengan el mejor puntaje de validación que, como bien sabemos, se mide como L1Loss. Vamos a entrenar el modelo en mini_batch de 10 secuencias (llegué a este número luego de varios intentos) y por 150 epochs.
model = LSTMAutoEncoder()
dm = ECGDataModule('ECG5000', normal_class = 1, batch_size = 10)
mc = ModelCheckpoint(
dirpath = 'checkpoints',
filename = 'best-checkpoint',
save_top_k = 1,
verbose = True,
monitor = 'val_loss',
mode = 'min')
# Instancia del Trainer
trainer = pl.Trainer(max_epochs = 150,
deterministic = True,
gpus = 1,
callbacks = [mc],
progress_bar_refresh_rate=20,
fast_dev_run = False)
GPU available: True, used: True
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
trainer.fit(model, dm)
LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]
| Name | Type | Params
--------------------------------------
0 | encoder | Encoder | 116 K
1 | decoder | Decoder | 132 K
2 | criterion | L1Loss | 0
--------------------------------------
249 K Trainable params
0 Non-trainable params
249 K Total params
0.998 Total estimated model params size (MB)
Eligiendo el Mejor Modelo
Una vez entrenado el modelo, cargo el modelo guardado en el mejor checkpoint:
trained_model = LSTMAutoEncoder.load_from_checkpoint(
"checkpoints/best-checkpoint.ckpt",
)
trained_model.freeze()
trained_model
LSTMAutoEncoder(
(encoder): Encoder(
(rnn1): LSTM(1, 128, batch_first=True)
(rnn2): LSTM(128, 64, batch_first=True)
)
(decoder): Decoder(
(rnn1): LSTM(64, 64, batch_first=True)
(rnn2): LSTM(64, 128, batch_first=True)
(dense_layers): Linear(in_features=128, out_features=1, bias=True)
)
(criterion): L1Loss()
)
La lógica para validar el funcionamiento del modelo es el siguiente:
- Voy a generar una predicción de cada uno de los dataset involucrados: train (lo normal), test (para chequear que el modelo funcione bien en data normal no vista) y en las anomalías.
- Un aspecto importante acá es que voy a tener que generar otro
Dataloaderque cargue mi data 1 a 1. Esto porque para determinar la anomalía necesito el error medido de cada muestra y, como mencioné anteriormente, el entrenamiento se hizo en batch nde 10 secuencias, y elL1Lossestá siendo agregado mediante un promedio (reduction = 'mean').
def plot_errors(model, data):
dl = DataLoader(data, batch_size = 1,
pin_memory = True,
num_workers = cpu_count(),
shuffle=False)
preds = trainer.predict(model = model, dataloaders = dl)
preds_losses = torch.tensor([item[1] for item in preds]).numpy()
sns.displot(preds_losses, bins = 50, kde = True, height = 8, aspect = 2)
return preds_losses
Recordar que en este caso no me interesa la predicción propiamente tal, sino que el error de reconstrucción. La premisa es que altos errores de reconstrucción implican una anomalía.
normal_loss = plot_errors(trained_model, dm.train_df)
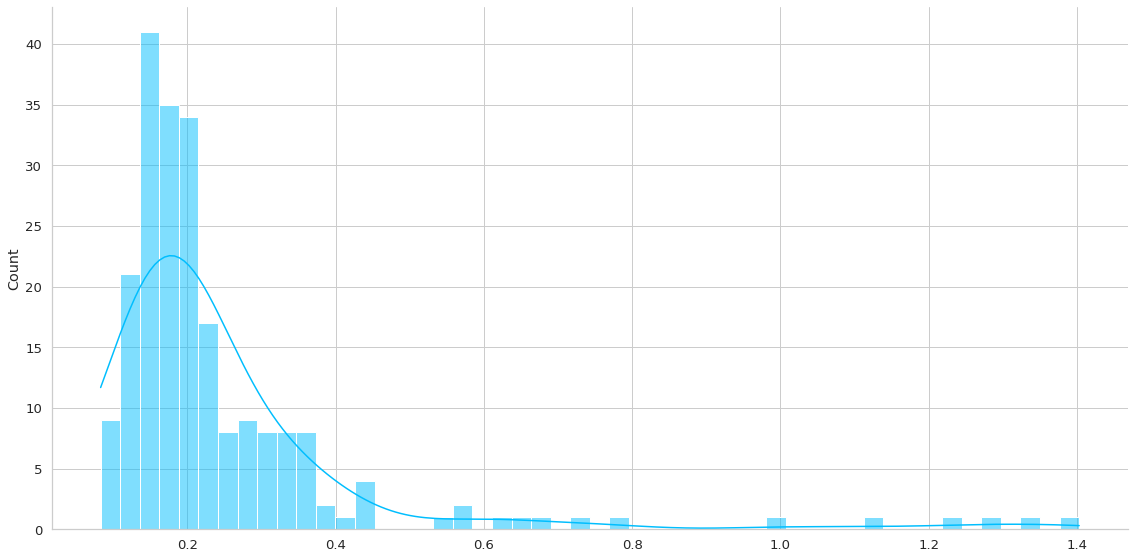
test_loss = plot_errors(trained_model, dm.test_df)
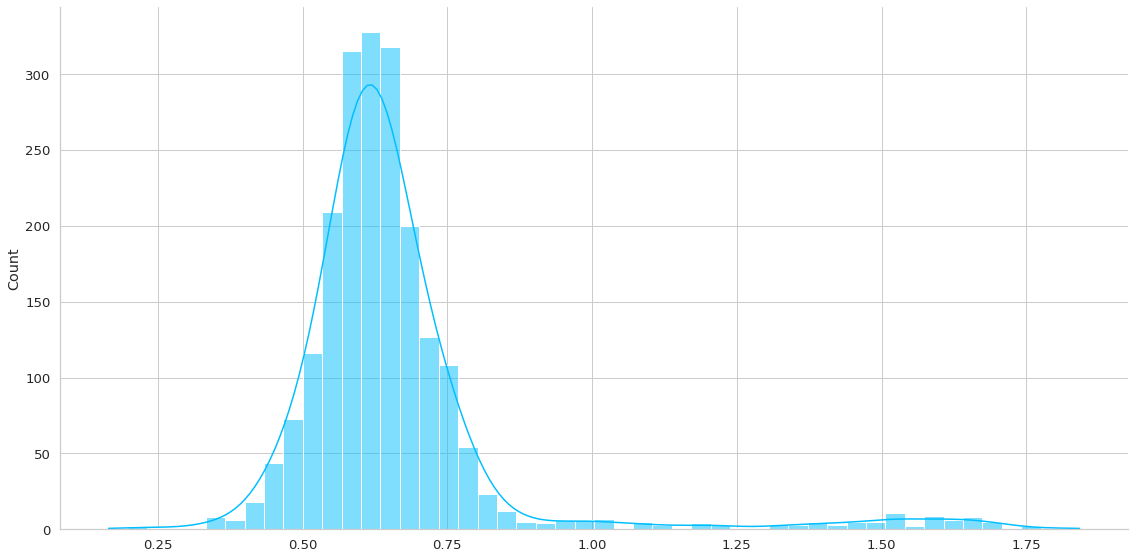
anomaly_loss = plot_errors(trained_model, dm.anomaly_df)
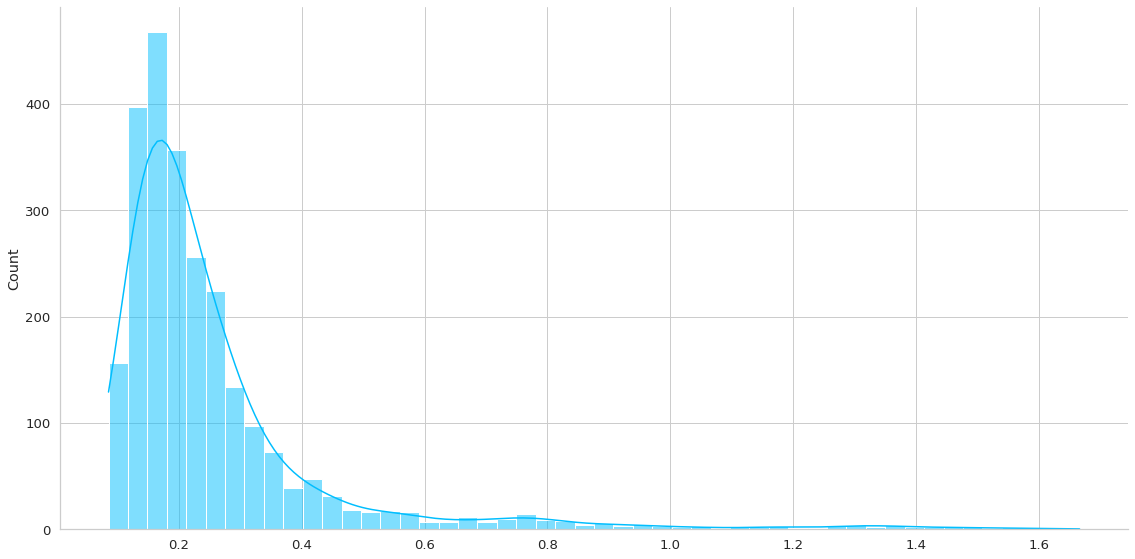
De la primera gráfica podemos ver una larga cola que representan los outliers, los casos más dificiles de recontruir. De acá podemos elegir un threshold que indique que un valor es un valor que sale de la normalidad. Por ejemplo en este caso podría ser 0.5. Por lo tanto vamos a decir que todo error de reconstrucción mayor a 0.5 será una anomalía en los otros datasets.
- Podemos ver que el segundo gráfico posee una distribución similar, con muy poquitos casos que tienen error sobre el 0.5.
- En el caso del tercer gráfico, que son los anomalías, éstas se distribuyen de manera bastante normal, pero con un error promedio mayor a 0.5. De hecho hay sólo una pequeña colita que es menor al threshold definido.
THRESHOLD = 0.5
Finalmente vamos a chequear el porcentaje de error de cada uno de los datasets a probar.
def check_correct(loss, treshold):
correct = sum(l <= THRESHOLD for l in loss)
print(f'Predicciones correctamente detectadas como normal: {correct}/{len(loss)}, {correct/len(loss)*100:.2f}%')
check_correct(normal_loss, THRESHOLD)
check_correct(test_loss, THRESHOLD)
check_correct(anomaly_loss, THRESHOLD)
Predicciones correctamente detectadas como normal: 2298/2481, 92.62%
Predicciones correctamente detectadas como normal: 205/219, 93.61%
Predicciones correctamente detectadas como normal: 153/2081, 7.35%
Se puede apreciar aproximadamente un error del 7% en todos los datasets:
- ~7% de los casos normales son categorizados como anómalos en el set de entrenamiento.
- ~7% de los casos normales son categorizados como anómalos en el set de testeo.
- 7.35% de los casos anómalos son considerados normales en el grupo de anomalías.
Conclusiones y próximos pasos
- Esta es una buena aplicación de la resolución de un problema con modelos no supervisados. Muchas veces nos quedamos sólo en el clustering y segmentaciones y hay harto más que puede ser explorado.
- Se pueden dar respuestas bien técnicas en un campo especializado incluso sin tener alto grado de conocimiento del tema.
- En este caso el
THRESHOLDes un valor fijo definido arbitrariamente por los resultados obtenidos, pero se pueden generar tramos tipos semáforo donde hay anomalías muy claras cuando el error es muy alto, pero otros casos más borrosos (con menos seguridad), cuando el error es bajo, que probablemente necesitan la intervención de un experto para ser correctamente diagnosticado. - En términos del modelo hay harto para mejorar. Se puede modificar la arquitectura y jugar un poco más con los hiperparámetros. En mi caso yo sólo modifiqué el
batch_sizecon el objetivo de disminuir el tiempo de entrenamiento y resultó que elbatch_sizelograba buen equilibrio entre tiempo de entrenamiento y resultados.
Espero que este tipo de modelos les parezca interesante.
Nos vemos en la otra,